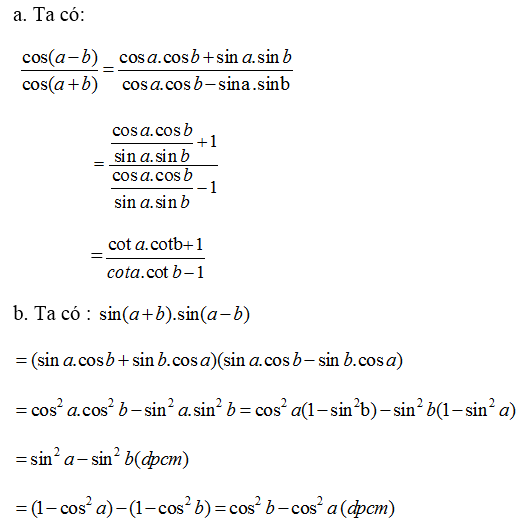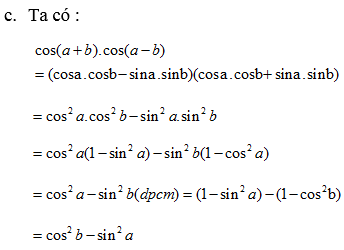Chứng minh rằng: \(cos\left(a+b\right)cos\left(a-b\right)=cos^2b-sin^2a\)
DH
Những câu hỏi liên quan
Chứng minh đẳng thức :
a) \(\dfrac{\cos\left(a-b\right)}{\cos\left(a+b\right)}=\dfrac{\cot a.\cot b+1}{\cot a.\cot b-1}\)
b) \(\sin\left(a+b\right)\sin\left(a-b\right)=\sin^2a-\sin^2b=\cos^2b-\cos^2a\)
c) \(\cos\left(a+b\right)\cos\left(a-b\right)=\cos^2a-\sin^2b=\cos^2b-\sin^2a\)
chứng minh:
a) \(\frac{cos\left(a-b\right)}{sin\left(a+b\right)}=\frac{cota.cotb+1}{cota.cotb-1}\)
b) sin(a+b).sin(a-b)=\(sin^2a-sin^2b=cos^2a-cos^2b\)
c) cos(a+b).cos(a-b)=\(cos^2a-sin^2b=cos^2b-sin^2a\)
\(\frac{cos\left(a-b\right)}{sin\left(a+b\right)}=\frac{cosa.cosb+sina.sinb}{sina.cosb+cosa.sinb}=\frac{\frac{cosa.cosb}{sina.sinb}+1}{\frac{sina.cosb}{sina.sinb}+\frac{cosa.sinb}{sina.sinb}}=\frac{cota.cotb+1}{cota+cotb}\)
Bạn ghi đề ko đúng
\(sin\left(a+b\right)sin\left(a-b\right)=\frac{1}{2}\left[cos2b-cos2a\right]\)
\(=\frac{1}{2}\left[1-2sin^2b-1+2sin^2a\right]\)
\(=sin^2a-sin^2b\)
\(=1-cos^2a-1+cos^2b=cos^2b-cos^2a\)
Câu này bạn cũng ghi đề ko đúng
\(cos\left(a+b\right)cos\left(a-b\right)=\frac{1}{2}\left[cos2a+cos2b\right]\)
\(=\frac{1}{2}\left[2cos^2a-1+1-2sin^2b\right]=cos^2a-sin^2b\)
\(=1-sin^2a-1+cos^2b=cos^2b-sin^2a\)
Đúng 0
Bình luận (0)
Cho: cosa, cosb ≠ 0, chứng minh đẳng thức: \(\frac{\sin\left(a+b\right).\sin\left(a-b\right)}{\cos^2a.\cos^2b}=\tan^2a-\tan^2b\)
Chứng minh rằng:
a) \(sin\left(a+b\right).sin\left(a-b\right)=sin^2a-sin^2b=cos^2b-cos^2a\)
b) \(4sin\left(x+\dfrac{\Pi}{3}\right).sin\left(x-\dfrac{\Pi}{3}\right)=4sin^2x-3\)
c) \(sin\left(x+\dfrac{\Pi}{4}\right)-sin\left(x-\dfrac{\Pi}{4}\right)=\sqrt{2}cosx\)
d) \(\dfrac{1}{sin10^0}-\dfrac{\sqrt{3}}{cos10^0}=4\)
Chứng minh các đẳng thức
1) tan2a - tan2b = \(\frac{sin\left(a+b\right)\cdot sin\left(a-b\right)}{cos^2a\cdot cos^2b}\)
2) \(\frac{tan\left(a-b\right)+tanb}{tan\left(a+b\right)-tanb}=\frac{cos\left(a+b\right)}{cos\left(a-b\right)}\)
1. Rút gọn biểu thức sau: C sin6xtimes cot3x-cos6x
2. Chứng minh các đẳng thức sau:
a) sqrt{2}sinleft(x-frac{pi}{4}right)sqrt{2}cosleft(x+frac{pi}{4}right)
b) frac{cosleft(a+bright)times cosleft(a-bright)}{sin^2a+sin^2b}cot^2atimes cot^2b-1
3. Cho Delta ABC. Chứng minh rằng: sinfrac{A}{2}cosfrac{B}{2}times cosfrac{C}{2}-sinfrac{C}{2}times cosfrac{B}{2}
4. Chứng minh: Nếu sina2sinleft(a+bright) thì tanleft(a+bright)frac{sina}{cosb-2}
MONG MỌI NGƯỜI GIÚP ĐỠ CHO MÌNH! CẢM ƠN RẤT NHIỀU!
Đọc tiếp
1. Rút gọn biểu thức sau: C = \(sin6x\times cot3x-cos6x\)
2. Chứng minh các đẳng thức sau:
a) \(\sqrt{2}sin\left(x-\frac{\pi}{4}\right)=\sqrt{2}cos\left(x+\frac{\pi}{4}\right)\)
b) \(\frac{cos\left(a+b\right)\times cos\left(a-b\right)}{sin^2a+sin^2b}=cot^2a\times cot^2b-1\)
3. Cho \(\Delta ABC\). Chứng minh rằng: \(sin\frac{A}{2}=cos\frac{B}{2}\times cos\frac{C}{2}-sin\frac{C}{2}\times cos\frac{B}{2}\)
4. Chứng minh: Nếu \(sina=2sin\left(a+b\right)\) thì \(tan\left(a+b\right)=\frac{sina}{cosb-2}\)
MONG MỌI NGƯỜI GIÚP ĐỠ CHO MÌNH! CẢM ƠN RẤT NHIỀU!
\(C=2sin3x.cos3x.\frac{cos3x}{sin3x}-\left(cos^23x-sin^23x\right)\)
\(=2cos^23x-cos^23x+sin^23x=cos^23x+sin^23x=1\)
\(\sqrt{2}sin\left(x-\frac{\pi}{4}\right)=\sqrt{2}\left(sinx.cos\frac{\pi}{4}-cosx.sin\frac{\pi}{4}\right)\)
\(=\sqrt{2}\left(sinx.sin\frac{\pi}{4}-cosx.cos\frac{\pi}{4}\right)=-\sqrt{2}\left(cosx.cos\frac{\pi}{4}-sinx.sin\frac{\pi}{4}\right)=-\sqrt{2}cos\left(x+\frac{\pi}{4}\right)\)
Câu này bạn ghi nhầm đề (lưu ý rằng \(sin\frac{\pi}{4}=cos\frac{\pi}{4}=\frac{\sqrt{2}}{2}\))
Câu 2b bạn cũng xem lại đề, chắc chắn ko đúng
\(\frac{A}{2}+\frac{B}{2}+\frac{C}{2}=90^0\Rightarrow sin\frac{A}{2}=cos\left(\frac{B}{2}+\frac{C}{2}\right)=cos\frac{B}{2}cos\frac{C}{2}-sin\frac{B}{2}sin\frac{C}{2}\)
Câu 3 bạn cũng ghi sai đề luôn
Trong 1 ngày đẹp trời thì câu 4 cũng sai luôn cho đỡ lạc lõng đồng đội:
\(sin\left(a+b-b\right)=sin\left(a+b\right)cosb-cos\left(a+b\right)sinb=2sin\left(a+b\right)\)
\(\Leftrightarrow sin\left(a+b\right)\left[cosb-2\right]=cos\left(a+b\right).sinb\)
\(\Leftrightarrow\frac{sin\left(a+b\right)}{cos\left(a+b\right)}=\frac{sinb}{cosb-2}\Leftrightarrow tan\left(a+b\right)=\frac{sinb}{cosb-2}\)
4 câu bạn ghi đúng đề bài duy nhất câu 1, kinh thiệt :(
Đúng 2
Bình luận (0)
Chứng minh|
a) cos(a+b)cos(a-b) = cos2a - sin2b
b)\(cos\left(\dfrac{\pi}{4}+a\right)cos\left(\dfrac{\pi}{4}-a\right)+\dfrac{1}{2}sin^2a=\dfrac{1}{2}cos^2a\)
Áp dụng công thức biến tích thành tổng:
\(cos\left(a+b\right).cos\left(a-b\right)=\dfrac{1}{2}\left(cos2a+cos2b\right)\)
\(=\dfrac{1}{2}\left(2cos^2a-1+1-2sin^2b\right)=\dfrac{1}{2}\left(2cos^2a-2sin^2b\right)\)
\(=cos^2a-sin^2b\)
\(cos\left(\dfrac{\pi}{4}+a\right).cos\left(\dfrac{\pi}{4}-a\right)+\dfrac{1}{2}sin^2a=\dfrac{1}{2}\left(cos\dfrac{\pi}{2}+cos2a\right)+\dfrac{1}{2}sin^2a\)
\(=\dfrac{1}{2}cos2a+\dfrac{1}{2}sin^2a=\dfrac{1}{2}\left(cos^2a-sin^2a\right)+\dfrac{1}{2}sin^2a\)
\(=\dfrac{1}{2}cos^2a\)
Đúng 0
Bình luận (0)
Rút gọn các biểu thức sau:
a, \(A=\sin^2\left(a-b\right)+\sin^2b+2\sin\left(a-b\right).\sin b.\cos a\)
b, \(B=\cos^2a+\cos^2\left(a+b\right)-2\cos a.\cos b.\cos\left(a+b\right)\)
Mọi người giúp mình với ạ!!!
\(A=\frac{1}{2}-\frac{1}{2}cos\left(2a-2b\right)+\frac{1}{2}-\frac{1}{2}cos2b+2sin\left(a-b\right)sinb.cosa\)
\(=1-\frac{1}{2}\left[cos\left(2a-2b\right)+cos2b\right]+2sin\left(a-b\right)sinb.cosa\)
\(=1-cosa.cos\left(a-2b\right)+2sin\left(a-b\right).sinb.cosa\)
\(=1-cosa\left[cos\left(a-2b\right)-2sin\left(a-b\right)sinb\right]\)
\(=1-cosa\left[cos\left(a-2b\right)+cosa-cos\left(a-2b\right)\right]\)
\(=1-cosa^2=sin^2a\)
Hoàn toàn tương tự:
\(B=1+cos\left(2a+b\right).cosb-2cosa.cosb.cos\left(a+b\right)\)
\(=1+cosb\left[cos\left(2a+b\right)-2cosa.cos\left(a+b\right)\right]\)
\(=1+cosb\left[cos\left(2a+b\right)-cos\left(2a+b\right)-cosb\right]\)
\(=1-cos^2b=sin^2b\)
Đúng 0
Bình luận (0)
tính giá trị các biểu thức sau:
a, \(A=\left(\sin a+\cos a\right)^2-2\sin a\cos a-1\)
b, \(B=\left(\sin a-\cos a\right)^2+2\sin a\cos a+1\)
c, \(C=\left(\sin a +\cos a\right)^2+\left(\sin a-\cos a\right)^2+2\)
d, \(D=\sin^2a.\cot^2a+\cos^2a.\tan^2a\)
~ ~ ~ Áp dụng đẳng thức \(\left(a+b\right)^2+\left(a-b\right)^2=2\left(a^2+b^2\right)\) ~ ~ ~
a)
\(\left(\sin\alpha+\cos\alpha\right)^2-2\sin\alpha\cos\alpha-1\)
\(=\left(\sin\alpha+\cos\alpha\right)^2-\left(2\sin\alpha\cos\alpha+\sin^2\alpha+\cos^2\alpha\right)\)
\(=\left(\sin\alpha+\cos\alpha\right)^2-\left(\sin\alpha+\cos\alpha\right)^2\)
= 0
b)
\(\left(\sin\alpha-\cos\alpha\right)^2+2\sin\alpha\cos\alpha+1\)
\(=\left(\sin\alpha-\cos\alpha\right)^2+2\sin\alpha\cos\alpha+\sin^2\alpha+\cos^2\alpha\)
\(=\left(\sin\alpha-\cos\alpha\right)^2+\left(\sin\alpha+\cos\alpha\right)^2\)
\(=2\left(\sin^2\alpha+\cos^2\alpha\right)\)
= 2
c)
\(\left(\sin\alpha+\cos\alpha\right)^2+\left(\sin\alpha-\cos\alpha\right)^2+2\)
\(=2\left(\sin^2\alpha+\cos^2\alpha\right)+2\)
= 4
d)
\(\sin^2\alpha\cot^2\alpha+\cos^2\alpha\tan^2\alpha\)
\(=\left(\sin\times\dfrac{\cos}{\sin}\right)^2+\left(\cos\times\dfrac{\sin}{\cos}\right)^2\)
= 1
Đúng 0
Bình luận (0)