cho tam giac abc CAN tai a .Biết b =70 độ . tinh c,a
H24
Những câu hỏi liên quan
a) tinh cua 1 tam giac can biet goc o day cua tam giac do bang 50 do
b)tinh goc o day cua 1tam giac can biet goc o dinh cua tam giac do bang 70 do
c)biet tam giac ABC can tai A, hay tinh so do goc B va goc C, theo so do cua goc A.
a: Số đo góc ở đỉnh là \(180^0-2\cdot50^0=80^0\)
b: Số đo góc ở đáy là \(\dfrac{180^0-70^0}{2}=55^0\)
c: Vì ΔABC cân tại A
nên \(\widehat{B}=\widehat{C}=\dfrac{180^0-\widehat{A}}{2}\)
Đúng 0
Bình luận (0)
cho tam giac abc can tai a co goc bac =50do tren tia doi cua tia bc lay diem d tren tia doi cua tia cb lay diem e sao cho bd =ba ce=ca tinh goc dae
cho tam giac abc deu ve ben ngoai tam giac cac tam giac abd vuong can tai b tam giac ace vuong can tai c tinh so goc nhon cua ade
XÉT \(\Delta ABC\)CÂN TẠI A
\(\Rightarrow\hept{\begin{cases}AB=AC\\\widehat{B}=\widehat{C}\end{cases}}\)
TA CÓ \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\left(Đ/L\right)\)
THAY\(50^0+\widehat{B}+\widehat{C}=180^o\)
\(\widehat{B}+\widehat{C}=130^o\)
MÀ\(\widehat{B}=\widehat{C}\)
\(\Rightarrow\widehat{B}=\widehat{C}=\frac{130^o}{2}=65^o\)
TA CÓ \(\widehat{DBA}+\widehat{ABC}=180^o\left(KB\right)\)
\(\Rightarrow\widehat{DBA}=180^o-65^o=115^o\)
TA CÓ\(\widehat{ACE}+\widehat{ACB}=180^o\left(KB\right)\)
\(\Rightarrow\widehat{ACE}=180^o-65^0=115^o\)
XÉT \(\Delta ACE\)CÓ AC=CE (GT) =>\(\Delta ACE\)CÂN TẠI C
\(\Rightarrow\widehat{CAE}=\widehat{AEC}=\frac{180^o-115^0}{2}=32,5^0\)
XÉT \(\Delta ABD\)CÓ AB=BD (GT) =>\(\Delta ABD\)CÂN TẠI B
\(\Rightarrow\widehat{DAB}=\widehat{ADB}=\frac{180^o-115^0}{2}=32,5^0\)
TA CÓ\(\widehat{DAB}+\widehat{BAC}+\widehat{EAC}=\widehat{DAE}\)
THAY\(32,5^o+50^0+32,5^0=\widehat{DAE}\)
\(\Rightarrow\widehat{DAE}=115^0\)
cho tam giac ABC can tai A co goc B=2A. phan giac B cat AC tai D
a, tinh so do cac goc cua tam giac ABC
b, CM: DA=DB
c, CM: DH=BC
cho tam giac abc can tai a, goc a =90 do, tinh goc b, c
ta co goc b = goc c (vi tam giac abc can tai a )= goc 180 do - goc a / 2 =180 do - 90 do /2=45 do.
Đúng 0
Bình luận (0)
Cho tam giac ABC can tai A co goc B=2A.ve phan giac BD a)tinh cac goc tam giac ABC b)chung minh:DA=BC
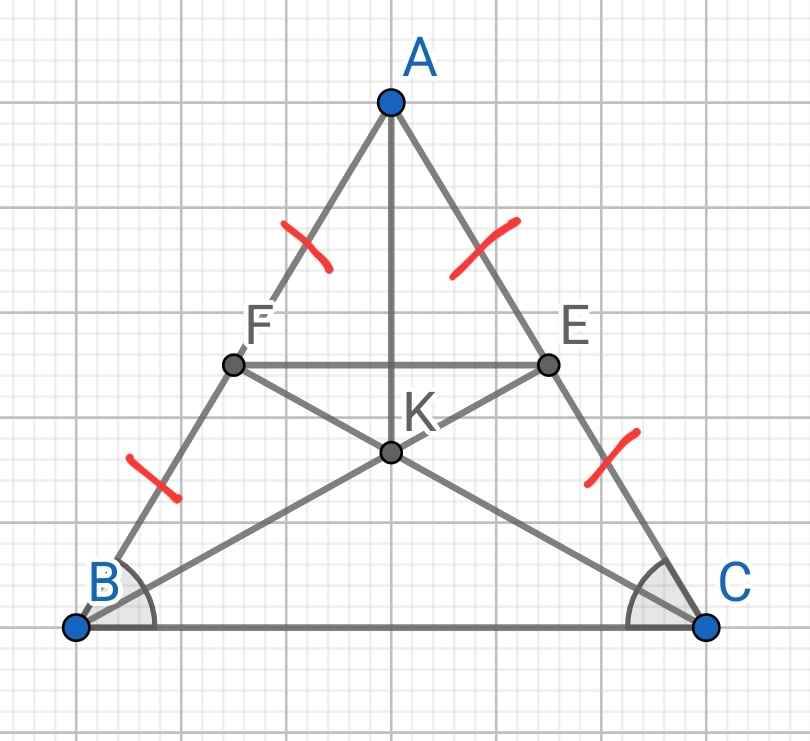
cho tam giac ABC can tai A.goi BE va CF la hai duong trung tuyen .giao diem BE va CF la K 1)cm a) BE =CF b) tam giac BKC can tai K c) FK=EK d) tam giac BKC = tam giac CEK ( TINH 7 CACH ) 2) ke doan thang EF . CM a) tam giac AEF can
b) EF//BC
3) ke doan thang AK .CM tam giac AFK = tam giac AEK
 1.
1.
a) Do ∆ABC cân tại A (gt)
⇒ AB = AC và ∠ABC = ∠ACB (1)
Do BE là đường trung tuyến của ∆ABC (gt)
⇒ E là trung điểm của AC
⇒ AE = CE = AC/2 (2)
Do CF là đường trung tuyến của ∆ABC (gt)
⇒ F là trung điểm của AB
⇒ AF = BF = AB/2 (3)
Từ (1), (2) và (3) ⇒ BF = CE
Do ∠ABC = ∠ACB (cmt)
⇒ ∠FBC = ∠ECB
Xét ∆BFC và ∆CEB có:
BF = CE (cmt)
∠FBC = ∠ECB (cmt)
BC chung
⇒ ∆BFC = ∆CEB (c-g-c)
⇒ CF = BE (hai cạnh tương ứng)
Hay BE = CF
b) Do ∆BFC = ∆CEB (cmt)
⇒ ∠BCF = ∠CBE (hai góc tương ứng)
⇒ ∠BCK = ∠CBK
∆BKC có:
∠BCK = ∠CBK (cmt)
⇒ ∆BKC cân tại K
c) Do ∆BKC cân tại K (cmt)
⇒ BK = CK
Do ∠ABC = ∠ACB (cmt)
⇒ ∠ABK = ∠ABC - ∠CBK = ∠ACB - ∠BCK = ∠ACK
⇒ ∠FBK = ∠ECK
Xét ∆BFK và ∆CEK có:
BK = CK (cmt)
∠FBK = ∠CEK (cmt)
BF = CE (cmt)
⇒ ∆BFK = ∆CEK (c-g-c)
⇒ FK = EK (hai cạnh tương ứng)
d) Sửa đề: Chứng minh ∆BFK = ∆CEK
Xét ∆BFK và ∆CEK có:
BK = CK (cmt)
BF = CE (cmt)
FK = EK (cmt)
⇒ ∆BFK = ∆CEK (c-c-c)
2.
a) Từ (1), (2) và (3) ⇒ AF = AE
∆AEF có:
AE = AF (cmt)
⇒ ∆AEF cân tại A
b) Do ∆ABC cân tại A (gt)
⇒ ∠ABC = ∠ACB = (180⁰ - ∠BAC) : 2 (4)
Do ∆AEF cân tại A (cmt)
⇒ ∠AFE = ∠AEF = (180⁰ - ∠FAE) : 2
⇒ ∠AFE = ∠AEF = (180⁰ - ∠BAC) : 2 (5)
Từ (4) và (5) ⇒ ∠ABC = ∠AFE
Mà ∠ABC và ∠AFE là hai góc đồng vị
⇒ EF // BC
c) Xét ∆AFK và ∆AEK có:
AF = AE (cmt)
AK chung
FK = EK (cmt)
⇒ ∆AFK = ∆AEK (c-c-c)
Đúng 0
Bình luận (0)
cho tam giac ABC can tai A ;AB=AC=17;BC=16. tinh duong cao AH va goc A, goc B cua tam giac ABC
AH là đường cao tam giác ABC cân tại A nên cũng là trung tuyến
\(\Rightarrow BH=HC=\dfrac{1}{2}BC=8\)
Ta có \(\cos\widehat{B}=\dfrac{BH}{AB}=\dfrac{8}{17}\approx\cos61^0\)
Do đó \(\widehat{B}=\widehat{C}\approx61^0\left(\Delta ABC.cân.tại.A\right)\)
Ta có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\Rightarrow\widehat{A}=180^0-2\cdot61^0=58^0\)
Ta có \(AH=\sin\widehat{B}\cdot AB=\sin61^0\cdot17\approx0,9\cdot17=15,3\)
Đúng 0
Bình luận (0)
Cho tam giac AMN can tai A:
a. A=70° . Tinh 2 goc con lai
b. M=40°. Tinh 2 goc con lai
a/Do A=70=> N+M=180-70=110 mak tam giác AMN cân tại A=> M=N=>M=N=110/2=55
b/ M=40 mak tam giác AMN cân tại A=> N=40
ta có A+M+N=180=> A=180-40-40=100
Mấy câu này dễ ợt
Đúng 0
Bình luận (0)
cho tam giac abc can tai a co goc a =20o ve d tren nua mat phang bo ac k chua diem b sao cho tam giac bcd can tai c va bcd=140o tinh adc


