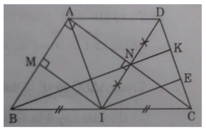
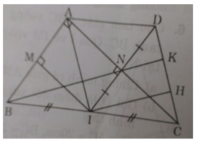
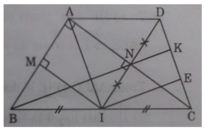
ΔABC ⊥A,(AB,AC).Gọi I là trung điểm BC. Qua I vẽ IM⊥AB(M∈AB);IN⊥AC(NϵAC).Gọi D là điểm đối xứng I qua N
a, C/m ADCI là hình thoi
b, Đường thẳng BN cắt CD ở K.Qua I kẻ đường thẳng // BK cắt CD ở E. C/m DK=KE=EC
Không cần vẽ hình đâu, các bạn giải giúp mik với. Mik đang cần gấp