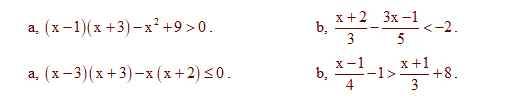Ôn tập chương II - Đa giác. Diện tích đa giác

ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC^2=8^2+6^2=100\)

=>\(BC=\sqrt{100}=10\left(cm\right)\)

Xét ΔBAC có BD là phân giác

nên \(\dfrac{AD}{AB}=\dfrac{CD}{CB}\)

=>\(\dfrac{AD}{8}=\dfrac{CD}{10}\)

=>\(\dfrac{AD}{4}=\dfrac{CD}{5}\)

mà AD+CD=AC=6cm(Do D nằm giữa A và C)

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{AD}{4}=\dfrac{CD}{5}=\dfrac{AD+CD}{4+5}=\dfrac{6}{9}=\dfrac{2}{3}\)

=>\(AD=4\cdot\dfrac{2}{3}=\dfrac{8}{3}\left(cm\right);CD=5\cdot\dfrac{2}{3}=\dfrac{10}{3}\left(cm\right)\)

Xét ΔCAB có CE là phân giác

nên \(\dfrac{AE}{AC}=\dfrac{BE}{BC}\)

=>\(\dfrac{AE}{6}=\dfrac{BE}{10}\)

=>\(\dfrac{AE}{3}=\dfrac{BE}{5}\)

mà AE+BE=AB=8cm(E nằm giữa A và B)

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{AE}{3}=\dfrac{BE}{5}=\dfrac{AE+BE}{3+5}=\dfrac{8}{8}=1\)

=>\(AE=3\cdot1=3cm;BE=5\cdot1=5cm\)

a: Xét tứ giác AEHF có

góc AEH=góc AFH=góc FAE=90 độ

=>AEHF là hình chữ nhật

b: FA=FD

FA=HE

=>HE=FD

Xét tứ giác HEFD có

HE//FD

HE=FD

=>HEFD là hình bình hành

c: Sửa đề: MP vuông góc AB

M đối xứng G qua AB

=>MG vuông góc AB tại trung điểm của MG

=>MG vuông góc AB tại P và P là trung điểm của MG

XétΔABC có

M là trung điểm của BC

MP//AC

=>P là trung điểm của AB

Xét tứ giác AMBG có

P là trung điểm chung của AB và MG

MA=MB

=>AMBG là hình thoi

M đối xứng K qua AC

=>MK vuông góc AC tại trung điểm của MK

=>Q là trung điểm của MK

Xét ΔABC có

M là trung điểm của BC

MQ//AB

=>Q là trung điểm của AC

Xét tứ giác AMCK có

Q là trung điểm chung của AC và MK

MA=MC

=>AMCK là hình thoi

`a, x^2 + 2x - 3 - x^2 + 9 >0`

`<=> 2x + 6 >0`

`<=> 2x > -6`

`<=> x > -3`.

`b, (x+2)/3 - (3x-1)/5 <-2`

`<=> (5x+10-9x+3)/15<-2`

`<=> -4x + 13 <-30`

`<=> -4x <-43`.

`<=> 4x > 43.`

`<=> x >43/4`.

`c, x^2-9 - x^2 - 2x <=0`

`<=> 9 + 2x >=0`

`<=> 2x >=-9`

`<=> x >=-9/2`.

`d, (x-1)/4 -1 > (x+1)/3 + 8`

`<=> (3x-3 -4x-4)/12>9`

`<=> -x - 7 >108`.

`<=> -x > 115`.

`<=> x <-115.`

a) \(\left(x-1\right)\left(x+3\right)-x^2+9>0\)

\(\Leftrightarrow\left(x-1\right)\left(x+3\right)-\left(x+3\right)\left(x-3\right)>0\)

\(\Leftrightarrow\left(x+3\right)\left[\left(x-1\right)-\left(x-3\right)\right]>0\)

\(\Leftrightarrow2\left(x+3\right)>0\)

\(\Leftrightarrow x+3>0\)

\(\Leftrightarrow x>-3\)

b) \(\dfrac{x+2}{3}-\dfrac{3x-1}{5}< -2\)

\(\Leftrightarrow\dfrac{5\left(x+2\right)}{15}-\dfrac{3\left(3x-1\right)}{15}< \dfrac{-2\cdot15}{15}\)

\(\Leftrightarrow5x+10-9x+3< -30\)

\(\Leftrightarrow-4x+13< -30\)

\(\Leftrightarrow-4x< -43\)

\(\Leftrightarrow x>\dfrac{43}{4}\)

\(a,\left(x-1\right)\left(x+3\right)-x^2+9>0\\ \Leftrightarrow x^2+2x-3-x^2+9>0\\ \Leftrightarrow2x>-6\\ \Leftrightarrow x>-3\)

\(b,\dfrac{x+2}{3}-\dfrac{3x-1}{5}< -2\\ \Leftrightarrow\dfrac{5\left(x+2\right)-3\left(3x-1\right)}{15}< -2\\ \Leftrightarrow5x+10-9x+3< -30\\ \Leftrightarrow-4x< -43\\ \Leftrightarrow x>\dfrac{43}{4}\)

\(a,\left(x-3\right)\left(x+3\right)-x\left(x+2\right)\le0\\ x^2-9-x^2-2x\le0\\ \Leftrightarrow-2x\le9\\ \Leftrightarrow x\ge-\dfrac{9}{2}\)

\(b,\dfrac{x-1}{4}-1>\dfrac{x+1}{3}+8\\ \Leftrightarrow\dfrac{3\left(x-1\right)-12-4\left(x+1\right)-8.12}{12}>0\\ \Leftrightarrow3x-3-12-4x-4-96>0\)

\(\Leftrightarrow-x>115\\ \Leftrightarrow x< -115\)

a: Xét tứ giác ABCD có

M là trung điểm chung của AC và BD

góc BAD=90 độ

=>ABCD là hình chữ nhật

b: Xét tứ giác EDBC có

ED//BC

ED=BC

=>EDBC là hình bình hành

=>Eb cắt CD tại trung điểm của mỗi đường

=>ID=IB

a: Xét ΔADB và ΔAEC có

góc ADB=góc AEC

góc DAB chung

=>ΔADB đồng dạng với ΔAEC

=>AD/AE=AB/AC

=>AD/AB=AE/AC

Xét ΔADE và ΔABC có

AD/AB=AE/AC

góc A chung

=>ΔADE đồng dạng với ΔABC

b: Xét ΔHEB vuông tại E và ΔHDC vuông tại D có

góc EHB=góc DHC

=>ΔHEB đồng dạng với ΔHDC

=>HE/HD=HB/HC

=>HE*HC=HB*HD

a: Xet ΔBHA vuông tại H và ΔBAC vuông tại A có

góc HBA chung

=>ΔBHA đồng dạng với ΔBAC

b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)

BD là phân giác

=>DA/AB=DC/BC

=>DA/3=DC/5=8/8=1

=>DA=3cm; DC=5cm

c: Xét ΔBAD vuông tại A và ΔBHI vuông tại H có

góc ABD=góc HBI

=>ΔBAD đồng dạng với ΔBHI

=>BA/BH=BD/BI

=>BA*BI=BD*BH

d: ΔBAD đồng dạng với ΔBHI

=>\(\dfrac{S_{BAD}}{S_{BHI}}=\left(\dfrac{BA}{BH}\right)^2=\left(\dfrac{6}{3.6}\right)^2=\dfrac{25}{9}\)

=>\(S_{BHI}=\dfrac{1}{2}\cdot6\cdot3:\dfrac{25}{9}=9\cdot\dfrac{9}{25}=\dfrac{81}{25}\)

Xét ΔACB có MN//BC

nên AN/AB=AM/AC
=>AM/35=2/5

=>AM=14cm

MN//BC

=>MN/BC=AN/AB=2/5

=>16/BC=2/5

=>BC=40cm

a: Xét ΔABD có AM/AB=AQ/AD

nên MQ//BD

Xét ΔCBD có CP/CD=CN/CB

nên PN//BD

=>MQ//PN

Xét ΔBAC có BN/BC=BM/BA

nên MN//AC

Xet ΔDAC có DP/DC=DQ/DA

nên PQ//AC

=>MN//PQ

mà MQ//NP

nên MNPQ là hình bình hành

b:

MQ/BD=AM/AB

=>MQ=AM/AB*BD

MN/AC=BM/BA

=>MN=AC*BM/BA=BD*BM/BA

 \(C_{MNPQ}=\left(MN+MQ\right)\)*2

\(=2\left(BD\cdot\dfrac{AM}{AB}+BD\cdot\dfrac{BM}{BA}\right)\)

=2BD

a: Xét ΔCAE có

CD là đường cao

CD là trung tuyến

CD=AE/2

Do đó:ΔCAE vuông cân tại C

b: Xét ΔHAB có HI/HA=HK/HE

nên IK//AE và IK=1/2AE

=>IK=AD=BC

Xét tứ giác BIKC có

IK//BC

IK=BC

Do đó: BIKC là hình bình hành