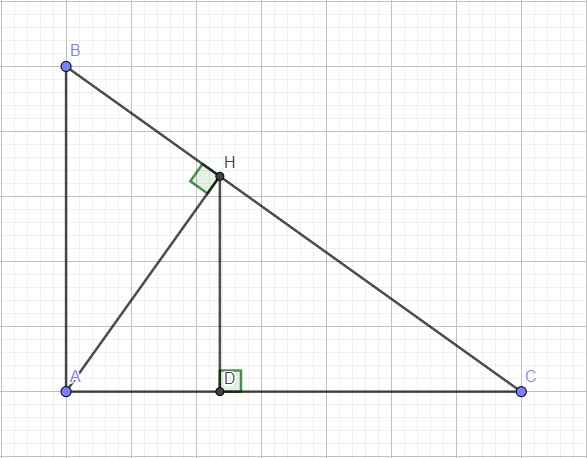
cho tam giác ABC vuông tại A có AB=3 AC=4. tính độ dài véc tơ BC giúp mình với ạ:(
LA
Những câu hỏi liên quan
Cho tam giác ABC vuông cân tại A có AB=AC=a. tính véc tơ AB, véc tơ AC; véc tơ AC, véc tơ CB
Đề bài có vấn đề. Bạn coi lại
Đúng 0
Bình luận (0)
giúp e với ạ
Cho tam giác ABC vuông tại A có BC=10 cm và AB:AC=3:4. Tính độ dài AB,AC
Áp dụng Pitago :
\(10^2=AB^2+AC^2\)
Ta có AB=3 và AC=4
=> 32+42=9+15=25=1/4(10^2)
=>AB=3 x 2 và AC =4x2
Thử :\(10^2=6^2+8^2\)
\(\Rightarrow100=36+84\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 5 Ac =6 góc A = 120 độ. Gọi N là điểm thoả mãn véc tơ NA + véc tơ 2AC = véc tơ 0. Gọi K là điểm trên cạnh BC sao cho véc tơ BK = x nhân véc tơ BC. Tìm x để AK vuông góc BN
Giúppp mình với mình đang cần bài rất gấp!!!
Cho tam giác ABC vuông tại A, đường cao AH=6cm, HC =8cm
a) tính độ dài HB,BC,AB,AC
b) Kẻ HD vuông góc với AC ( D thuộc AC). Tính độ dài HD và diện tích tam giác AHD
giúp mình với ạ
Áp dụng định lý Pitago cho tam giác vuông ACH:
\(AC=\sqrt{AH^2+HC^2}=10\left(cm\right)\)
Áp dụng hệ thức lượng cho tam giác vuông ABC:
\(AC^2=CH.BC\Rightarrow BC=\dfrac{AC^2}{CH}=\dfrac{25}{2}\) (cm)
\(\Rightarrow BH=BC-CH=\dfrac{9}{2}\left(cm\right)\)
Pitago tam giác vuông ABC:
\(AB=\sqrt{BC^2-AC^2}=\dfrac{15}{2}\left(cm\right)\)
b.
Áp dụng hệ thức lượng cho tam giác vuông ACH:
\(HD.AC=AH.HC\Rightarrow HD=\dfrac{AH.HC}{AC}=\dfrac{24}{5}\left(cm\right)\)
Tiếp tục là hệ thức lượng:
\(AH^2=AD.AC\Rightarrow AD=\dfrac{AH^2}{AC}=\dfrac{18}{5}\left(cm\right)\)
\(S_{AHD}=\dfrac{1}{2}AD.HD=\dfrac{216}{25}\left(cm^2\right)\)
Đúng 3
Bình luận (0)
1)Cho tam giác ABC vuông tại A.Biết góc B=60 độ;BC=4.Tính AB,AC,chiều cao AH
2)Cho tam giác ABC vuông tại A.Biết AB=2;góc C=45 độ.Tính AC,BC,chiều cao AH
3)Cho tam giác ABC vuông tại A,Biết AB=3;AC=4.Tính sin C,tan B
Giải giúp mình ạ
Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm. Đường cao AH(H thuộc BC); Tia phân giác góc A cắt BC tại D.
a)Chứng minh tam giác HAC đồng dạng tam giác HBA
b)Tính độ dài đoạn thẳng AD
Giải giúp mình câu b với ạ
Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm. Đường cao AH(H thuộc BC); Tia phân giác góc A cắt BC tại D.
a)Chứng minh tam giác HAC đồng dạng tam giác HBA
b)Tính độ dài đoạn thẳng AD
Giải giúp mình câu b với ạ
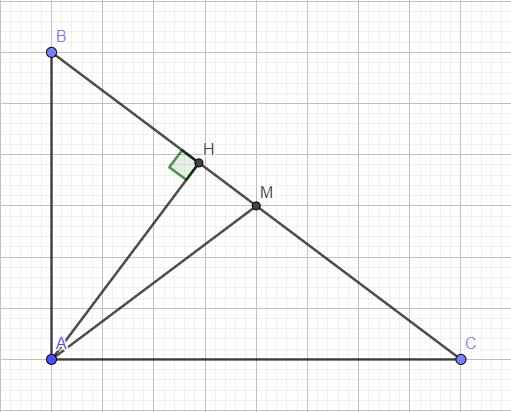
Cho tam giác ABC vuông tại A, AH vuông góc với BC,M là trung điểm của BC, biết AB=3,AC=4.Tính độ dài HM, mong mn giúp mình
Áp dụng định lý Pitago:
\(BC=\sqrt{AB^2+AC^2}=5\)
Trong tam giác vuông ABC, AM là trung tuyến ứng với cạnh huyền
\(\Rightarrow AM=\dfrac{1}{2}BC=\dfrac{5}{2}\)
Áp dụng hệ thức lượng:
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{12}{5}\)
Áp dụng định lý Pitago cho tam giác vuông AHM:
\(HM=\sqrt{AM^2-AH^2}=\dfrac{7}{10}\)
Đúng 1
Bình luận (0)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{1}{3^2}+\dfrac{1}{4^2}=\dfrac{25}{144}\)
\(\Leftrightarrow AH^2=\dfrac{144}{25}\)
hay AH=2,4(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
Ta có: ΔABC vuông tại A(gt)
mà AM là đường trung tuyến ứng với cạnh huyền BC(gt)
nên \(AM=\dfrac{BC}{2}=\dfrac{5}{2}=2.5\left(cm\right)\)
Áp dụng định lí Pytago vào ΔAMH vuông tại H, ta được:
\(AM^2=AH^2+HM^2\)
\(\Leftrightarrow HM^2=AM^2-AH^2=2.5^2-2.4^2=0.49\)
hay HM=0,7(cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có góc A = 120 độ, BC = 2BH, BH vuông góc với AC (H thuộc AC). Tính độ dài các đoạn thẳng HB, AC
Mn giúp mình với ạ