Giả sử f(x)=\(^{\left(X^3+3x+1935\right)^{2012}}\)
Tinh f(a) biết a=4
Giúp mình với !
DM
Những câu hỏi liên quan
cho \(f\left(x\right)=\dfrac{x^3}{1-3x-3x^2}\). hãy tính giá trị biểu thức sau: \(A=f\left(\dfrac{1}{2012}\right)+f\left(\dfrac{2}{2012}\right)+...+f\left(\dfrac{2010}{2012}\right)+f\left(\dfrac{2011}{2012}\right)\)
Bạn kiểm tra lại đề, \(f\left(x\right)=\dfrac{x^3}{1-3x-3x^2}\) hay \(f\left(x\right)=\dfrac{x^3}{1-3x+3x^2}\)
Đúng 1
Bình luận (0)
Cho \(f\left(x\right)=\frac{x^3}{1-3x+3x^2}\)hãy tính giá trị biểu thức
\(A=f\left(\frac{1}{2012}\right)+f\left(\frac{2}{2012}\right)+...+f\left(\frac{2010}{2012}\right)+f\left(\frac{2011}{2012}\right)\)
Ta xét : \(f\left(x\right)+f\left(1-x\right)=\frac{x^3}{1-3x+3x^2}+\frac{\left(1-x\right)^3}{1-3\left(1-x\right)+3\left(1-x\right)^2}\)
\(=\frac{x^3}{1-3x+3x^2}+\frac{\left(1-x\right)^3}{3x^2-3x+1}=\frac{\left(x+1-x\right)\left(x^2+x^2-2x+1+x^2-x\right)}{3x^2-3x+1}=\frac{3x^2-3x+1}{3x^2-3x+1}=1\)
Áp dụng ta có :
\(A=\left[f\left(\frac{1}{2012}\right)+f\left(\frac{2011}{2012}\right)\right]+\left[f\left(\frac{2}{2012}\right)+f\left(\frac{2010}{2012}\right)\right]+...+\left[f\left(\frac{1006}{2012}\right)+f\left(\frac{1006}{2012}\right)\right]\)
\(=1+1+...+1\)(Có tất cả 1006 số 1)
\(=1006\)
Đúng 0
Bình luận (0)
cho \(f\left(x\right)=\dfrac{x^3}{1-3x+3x^2}\) hãy tính giá trị của biểu thức sau:
\(A=f\left(\dfrac{1}{2012}\right)+f\left(\dfrac{2}{2012}\right)+...+f\left(\dfrac{2010}{2012}\right)+f\left(\dfrac{2011}{2012}\right)\)
Cho f(x)=\(\frac{^{x^3}}{1-3x+3x^2}\) .Tính giá trị biểu thức sau
A= f\(\left(\frac{1}{2012}\right)\)+f\(\left(\frac{2}{2012}\right)\)+...+f\(\left(\frac{2011}{2012}\right)\)
Đễ dàng chưng minh được
\(f\left(1-x\right)=1-f\left(x\right)\)
\(\Rightarrow f\left(1-x\right)+f\left(x\right)=1\)
\(\Rightarrow A=\left[f\left(\frac{1}{2012}\right)+f\left(\frac{2011}{2012}\right)\right]+\left[f\left(\frac{2}{2012}\right)+f\left(\frac{2010}{2012}\right)\right]+...+\left[f\left(\frac{1005}{2012}\right)+f\left(\frac{1007}{2012}\right)\right]+f\left(\frac{1006}{2012}\right)\)
\(=1005+f\left(\frac{1006}{2012}\right)\)
Làm nôt
Đúng 0
Bình luận (0)
1. Xác định các đa thức sau:a) Nhị thức bậc nhất f(x) ax + b với a≠0, biết f(-1) 1 và f(1) -1b) Tam thức bậc hai gleft(xright)ax^2+bx+c với a≠0, biết g(-2) 9, g(-1) 2, g(1)62.a) Đa thức f(x) ax + b (a≠0). Biết f(0) 0. Chứng minh f(x) -f(-x) với mọi x b) Đa thức f(x) ax2 + bx + c (a≠0). Biết f(1) f(-1). Chứng minh f(x) f(-x) với mọi x.3. Tìm tổng các hệ số của đa thức sau khi phá ngoặc và sắp xếp, biết:a) Đa thức fleft(xright)left(2x^3-3x^2+2x+1right)^{10}b) Đa thức gleft(xright)left...
Đọc tiếp
1. Xác định các đa thức sau:
a) Nhị thức bậc nhất f(x) = ax + b với a≠0, biết f(-1) = 1 và f(1) = -1
b) Tam thức bậc hai \(g\left(x\right)=ax^2+bx+c\) với a≠0, biết g(-2) = 9, g(-1) = 2, g(1)=6
2.a) Đa thức f(x) = ax + b (a≠0). Biết f(0) = 0. Chứng minh f(x) = -f(-x) với mọi x
b) Đa thức f(x) = ax2 + bx + c (a≠0). Biết f(1) = f(-1). Chứng minh f(x) = f(-x) với mọi x.
3. Tìm tổng các hệ số của đa thức sau khi phá ngoặc và sắp xếp, biết:
a) Đa thức \(f\left(x\right)=\left(2x^3-3x^2+2x+1\right)^{10}\)
b) Đa thức \(g\left(x\right)=\left(3x^2-11x+9\right)^{2011}.\left(5x^4+4x^3+3x^2-12x-1\right)^{2012}\)
1.a) Theo đề bài,ta có: \(f\left(-1\right)=1\Rightarrow-a+b=1\)
và \(f\left(1\right)=-1\Rightarrow a+b=-1\)
Cộng theo vế suy ra: \(2b=0\Rightarrow b=0\)
Khi đó: \(f\left(-1\right)=1=-a\Rightarrow a=-1\)
Suy ra \(ax+b=-x+b\)
Vậy ...
Đúng 0
Bình luận (0)
Tớ nêu hướng giải bài 3 thôi nhé:
Bài toán: Cho đa thức \(f\left(x\right)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0\)
Chứng minh tổng các hệ số của đa thức f(x) là giá trị của đa thức khi x = 1
Lời giải:
Thật vậy,thay x = 1 vào:
\(f\left(1\right)=a_n+a_{n-1}+...+a_1+a_0\) (đúng bằng tổng các hệ số của đa thức)
Vậy tổng các hệ số của 1 đa thức chính là giá trị của đa thức đó khi x = 1 (đpcm)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a, chứng minh đẳng thức
\(x^n-y^n=\left(x-y\right)\left(x^{n-1}+x^{n-2}y+x^{n-3}y^2+...+xy^{n-2}+y^{n-1}\right)\)
b, cho F(x) là đa thức với các hệ số nguyện. giả sử F(2011) và F(2012) là các số nguyên lẻ. chứng minh đa thức F(x) không có nghiệm nguyên
Cho \(F\left(x\right)=x^3-3x^2+3x+3\)
CM: \(f\left(\dfrac{2014}{2013}\right)< f\left(\dfrac{2013}{2012}\right)\)
\(f\left(x\right)=x^3-3x^2+3x+3=\left(x-1\right)^3+2\)
Thay vào là OK!!
Đúng 0
Bình luận (0)
Cho hàm số fleft( x right) x + 1 với x in mathbb{R}.a) Giả sử {x_0} in mathbb{R}. Hàm số fleft( x right) có liên tục tại điểm {x_0} hay không?b) Quan sát đồ thị hàm số fleft( x right) x + 1 với x in mathbb{R} (Hình 13), nếu nhận xét về đặc điểm của đồ thị hàm số đó.
Đọc tiếp
Cho hàm số \(f\left( x \right) = x + 1\) với \(x \in \mathbb{R}.\)
a) Giả sử \({x_0} \in \mathbb{R}.\) Hàm số \(f\left( x \right)\) có liên tục tại điểm \({x_0}\) hay không?
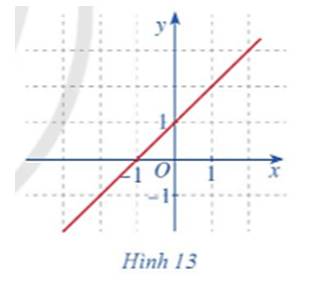
b) Quan sát đồ thị hàm số \(f\left( x \right) = x + 1\) với \(x \in \mathbb{R}\) (Hình 13), nếu nhận xét về đặc điểm của đồ thị hàm số đó.
a) Ta có \(f\left( {{x_0}} \right) = {x_0} + 1;\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( {x + 1} \right) = \mathop {\lim }\limits_{x \to {x_0}} x + 1 = {x_0} + 1\)
\( \Rightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Vậy hàm số \(f\left( x \right)\) liên tục tại \({x_0}.\)
b) Dựa vào đồ thị hàm số ta thấy: Đồ thị hàm số là một đường thẳng liền mạch với mọi giá trị \(x \in \mathbb{R}.\)
Đúng 0
Bình luận (0)
1. Cho fleft(xright)x^{2n}-x^{2n-1}+x^{2n-2}-...+x^2-x+1
gleft(xright)1-x+x^2-...+x^{2n-2}-x^{2n-1}+x^{2n}
Tính giá trị của đa thức h(x) tại x2012, biết hleft(xright)left(fleft(xright)+gleft(xright)right).left(gleft(xright)-fleft(xright)right)
2. Xác định các đa thức sau:
a) Nhị thức bậc nhất f(x) ax + b với ane0, biết f(-1) 1 và f(1) -1
b) Tam thức bậc hai gleft(xright)ax^2+bx+c với ane0, biết g(-2) 9, g(-1) 2, g(1)6
3. a) Đa thức f(x) ax + b left(ane0right). Biết f(0) 0...
Đọc tiếp
1. Cho \(f\left(x\right)=x^{2n}-x^{2n-1}+x^{2n-2}-...+x^2-x+1\)
\(g\left(x\right)=1-x+x^2-...+x^{2n-2}-x^{2n-1}+x^{2n}\)
Tính giá trị của đa thức h(x) tại x=2012, biết \(h\left(x\right)=\left(f\left(x\right)+g\left(x\right)\right).\left(g\left(x\right)-f\left(x\right)\right)\)
2. Xác định các đa thức sau:
a) Nhị thức bậc nhất f(x) = ax + b với \(a\ne0\), biết f(-1) = 1 và f(1) = -1
b) Tam thức bậc hai \(g\left(x\right)=ax^2+bx+c\) với \(a\ne0\), biết g(-2) = 9, g(-1) = 2, g(1)=6
3. a) Đa thức f(x) = ax + b \(\left(a\ne0\right)\). Biết f(0) = 0. Chứng minh f(x) = -f(-x) với mọi x
b) Đa thức f(x) = ax2 + bx + c \(\left(a\ne0\right)\). Biết f(1) = f(-1). Chứng minh f(x) = f(-x) với mọi x.