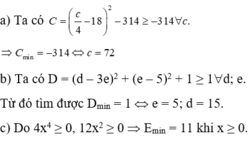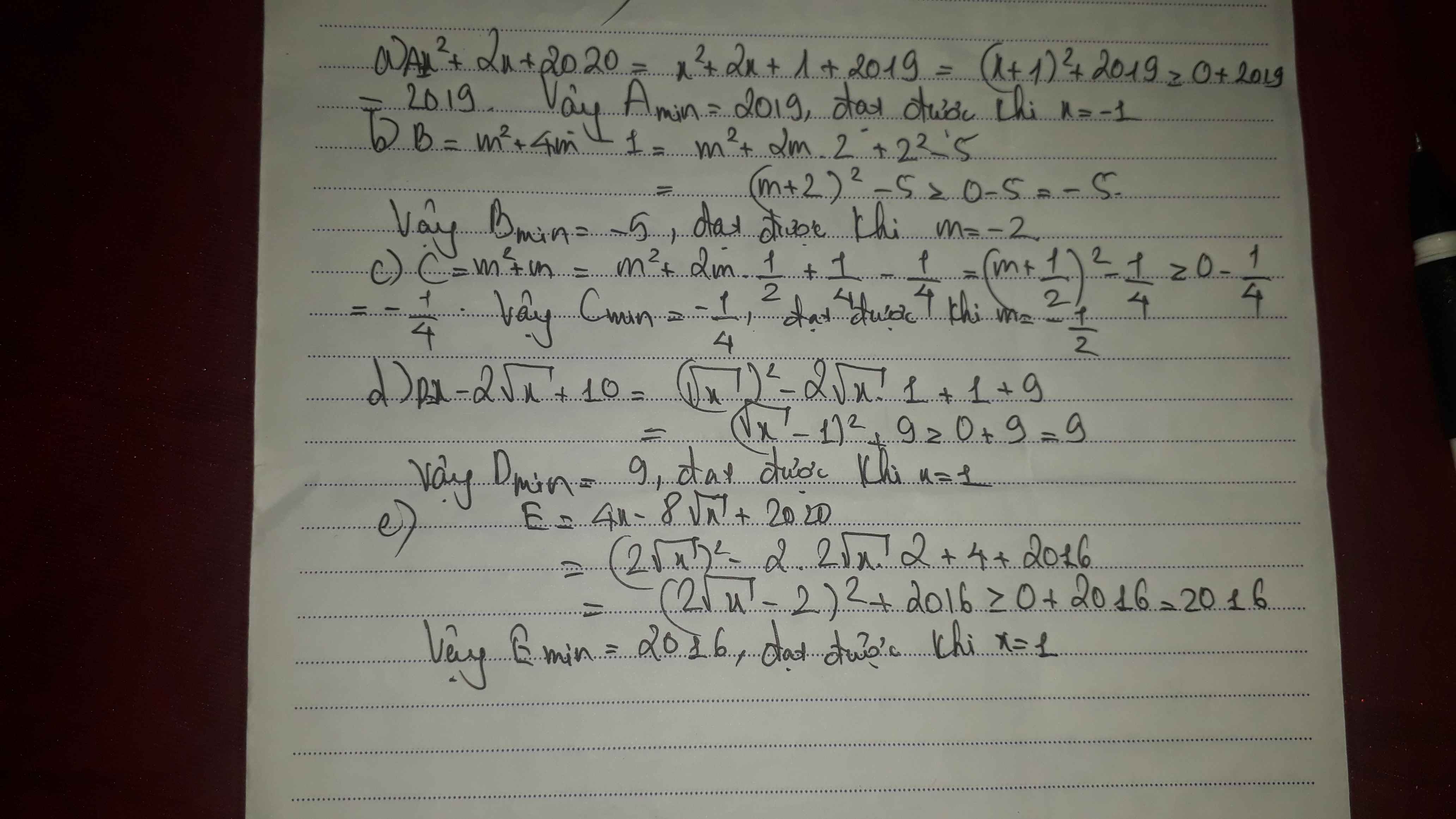Tìm GTNN của: \(D=d^2+10e^2-6de-10e+26\)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
VT
Những câu hỏi liên quan
Tìm GTNN của:\(D=d^2+10e^2-6de-10e+26\)
Ta có \(D=d^2+10e^2-6de-10e+26\)
\(D=d^2-6de+\left(3e\right)^2+4e^2-10e+26\)
\(D=\left(d-3e\right)^2+4\left(e^2-\frac{5}{2}e+26\right)\)
\(D=\left(d-3e\right)^2+4\left[e^2-2e.\frac{5}{4}+\left(\frac{5}{4}\right)^2+\frac{391}{16}\right]\)
\(D=\left(d-3e\right)^2+4\left[\left(e-\frac{5}{4}\right)^2+\frac{391}{16}\right]\)
\(D=\left(d-3e\right)^2+4\left(e-\frac{5}{4}\right)^2+\frac{391}{4}\)
Mà \(\left(e-\frac{5}{4}\right)^2\ge0\). Dấu "=" xảy ra khi và chỉ khi \(e=\frac{5}{4}\)
\(\left(d-3e\right)^2\ge0\). Dấu "=" xảy ra khi và chỉ khi \(d-3e=0\)=> \(d=\frac{15}{4}\)
=> \(\left(d-3e\right)^2+\left(e-\frac{5}{4}\right)^2+\frac{391}{4}\ge\frac{391}{4}\). Dấu "=" xảy ra khi và chỉ khi \(\hept{\begin{cases}d=\frac{15}{4}\\e=\frac{5}{4}\end{cases}}\)
Vậy GTNN của D là \(\frac{391}{14}\)khi \(\hept{\begin{cases}d=\frac{15}{4}\\e=\frac{5}{4}\end{cases}}\)
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của các biểu thức sau:
a) C=1/16c^2 -9c +10
b)D=d^2 +10e^2 -6de -10e +26
c) E=4x^2+12x+11
giúp mk với các bạn ơi, thứ 5 mk phải học rồi!
Con a) Đang nghĩ
b) D = d2 + 10e2 - 6de - 10e + 26
D= d2 - 2.3de + ( 3e)2 + e2 - 2.5e + 52 + 1
D= ( d - 3e)2 + ( e - 5)2 + 1
Do : ( d - 3e)2 lớn hơn hoặc bằng 0 với moi d, e
( e - 5)2 lớn hơn hoặc bằng 0 với mọi e
Vậy : ( d - 3e)2 + 1 lớn hơn hoặc bằng 1 với moi d, e
( e - 5)2 + 1 lớn hơn hoặc bằng 1 với mọi e
Vậy Dmin = 1 khi e = 5 . d = 15
c) E = 4x2 + 12x + 11
E = ( 2x)2 + 2.2x.3 + 32 + 2
E= ( 2x + 3)2 + 2
Do : ( 2x + 3)2 lớn hơn hặc bằng 0 với mọi x
--> ( 2x + 3)2 + 2 lớn hơn hặc bằng 2 với mọi x
Vậy , Emin = 2 KHI VÀ CHỈ KHI \(\dfrac{-3}{2}\)
Đúng 0
Bình luận (4)
Mn giúp em với
A 1/16c^2 -9c+10
B d^2+10e^2-6de-10e+26
C 4x^4+12x^2+11
đề bài là tìm giá trị nhỏ nhất của các biểu thức sau ạ, cíu em với, tối nay phải nộp r;-;
\(A=\dfrac{1}{16}c^2-9c+10=\dfrac{1}{16}\left(x-72\right)^2-314\ge-314\)
\(A_{min}=-314\) khi \(c=72\)
\(B=\left(d^2-6de+9e^2\right)+\left(e^2-10e+25\right)+1=\left(d-3e\right)^2+\left(e-5\right)^2+1\ge1\)
\(B_{min}=1\) khi \(\left\{{}\begin{matrix}d=15\\e=5\end{matrix}\right.\)
\(C=4x^4+12x^2+11\)
Do \(\left\{{}\begin{matrix}x^4\ge0\\x^2\ge0\end{matrix}\right.\) ; \(\forall x\Rightarrow C\ge11\)
\(C_{min}=11\) khi \(x=0\)
Đúng 5
Bình luận (0)
a) Ta có: \(\dfrac{1}{16}c^2-9c+10\)
\(=\left(\dfrac{1}{4}c\right)^2-2\cdot\dfrac{1}{4}c\cdot18+324-314\)
\(=\left(\dfrac{1}{4}c-18\right)^2-314\ge-314\forall c\)
Dấu '=' xảy ra khi \(\dfrac{1}{4}c=18\)
hay c=72
Vậy: Giá trị nhỏ nhất của biểu thức \(\dfrac{1}{16}c^2-9c+10\) là -314 khi c=72
b) Ta có: \(d^2+10e^2-6de-10e+26\)
\(=d^2-6de+9e^2+e^2-10e+25+1\)
\(=\left(d-3e\right)^2+\left(e-5\right)^2+1\ge1\forall d,e\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}e=5\\d=3e=3\cdot5=15\end{matrix}\right.\)
Vậy: Giá trị nhỏ nhất của biểu thức \(d^2+10e^2-6de-10e+26\) là 1 khi e=5 và d=15
c) Ta có: \(4x^4+12x^2+11\)
\(=4x^4+12x^2+9+2\)
\(=\left(2x^2+3\right)^2+2\ge3^2+2=11\)
Dấu '=' xảy ra khi x=0
Vậy: Giá trị nhỏ nhất của biểu thức \(4x^4+12x^2+11\) là 11 khi x=0
Đúng 5
Bình luận (1)
Tìm giá trị nhỏ nhất của các biểu thức sau:a) C
1
16
c
2
−
9
c
+
10
;
b) D
d
2
+ 10
e
2
– 6de – 10e + 26;c) E 4
x
4
+ 12
x
2
+ 11.
Đọc tiếp
Tìm giá trị nhỏ nhất của các biểu thức sau:
a) C = 1 16 c 2 − 9 c + 10 ; b) D = d 2 + 10 e 2 – 6de – 10e + 26;
c) E = 4 x 4 + 12 x 2 + 11.
Tìm giá trị nhỏ nhất
A=\(\frac{1}{16}\)\(c^2\)-9c+10
B=\(d^2\)+10\(e^2\)-6de-10e+26
\(A=\frac{1}{16}c^2-9c+10\)
\(A=\left(\frac{1}{16}c^2-9c+324\right)-314\)
\(A=\left(\frac{1}{4}c-18\right)^2-314\)
Mà \(\left(\frac{1}{4}c-18\right)^2\ge0\forall c\)
\(\Rightarrow A\ge-314\)
Dấu "=" xảy ra khi : \(\frac{1}{4}c-18=0\Leftrightarrow c=72\)
Vậy ...
\(B=d^2+10e^2-6de-10e+26\)
\(B=\left(d^2-6de+9e^2\right)+\left(e^2-10e+25\right)+1\)
\(B=\left(d-3e\right)^2+\left(e-5\right)^2+1\)
Mà \(\left(d-3e\right)^2\ge0\forall d;e\)
\(\left(e-5\right)^2\ge0\forall e\)
\(\Rightarrow B\ge1\)
Dấu "=" xảy ra khi : \(\hept{\begin{cases}d-3e=0\\e-5=0\end{cases}}\Leftrightarrow\hept{\begin{cases}d=15\\e=5\end{cases}}\)
Vậy ...
Đúng 0
Bình luận (0)
a, \(A=\frac{1}{16}c^2-9c+10=\left(\frac{1}{16}c^2-9c+324\right)-314=\left(\frac{1}{4}c-18\right)^2-314\ge-314\)
Dấu "=" xảy ra khi \(\frac{1}{4}c-18=0\Leftrightarrow c=72\)
Vậy Amin = -314 khi c = 72
b, \(B=d^2+10e^2-6de-10e+26\)
\(=\left(d^2-6de+9e^2\right)+\left(e^2-10e+25\right)+1\)
\(=\left(d-3e\right)^2+\left(e-5\right)^2+1\ge1\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}d-3e=0\\e-5=0\end{cases}\Leftrightarrow\hept{\begin{cases}d-15=0\\e=5\end{cases}\Leftrightarrow}\hept{\begin{cases}d=15\\e=5\end{cases}}}\)
Vậy Bmin = 1 khi d = 15, e = 5
Đúng 0
Bình luận (0)
Bài 1: Tìm giá trị lớn nhất của biểu thức sau:
a) \(A=8a-8a^2+3\)
b) \(B=b-\frac{9b^2}{25}\)
Bài 2: Tìm giá trị nhỏ nhất của các biểu thức sau:
a) \(C=\frac{1}{16}c^2-9c+10\)
b) \(D=d^2+10e^2-6de-10e+26\)
c) \(E=4x^4+12x^2+11\)
1. a. \(A=8a-8a^2+3=-8\left(a-\frac{1}{2}\right)^2+5\)
Vì \(\left(a-\frac{1}{2}\right)^2\ge0\forall a\)\(\Rightarrow-8\left(a-\frac{1}{2}\right)^2+5\le5\)
Dấu "=" xảy ra \(\Leftrightarrow-8\left(a-\frac{1}{2}\right)^2=0\Leftrightarrow a-\frac{1}{2}=0\Leftrightarrow a=\frac{1}{2}\)
Vậy Amax = 5 <=> a = 1/2
b. \(B=b-\frac{9b^2}{25}=-\frac{9}{25}\left(b-\frac{25}{18}\right)^2+\frac{25}{36}\)
Vì \(\left(b-\frac{25}{18}\right)^2\ge0\forall b\)\(\Rightarrow-\frac{9}{25}\left(b-\frac{25}{18}\right)^2+\frac{25}{36}\le\frac{25}{36}\)
Dấu "=" xảy ra \(\Leftrightarrow-\frac{9}{25}\left(b-\frac{25}{18}\right)^2=0\Leftrightarrow b-\frac{25}{18}=0\Leftrightarrow b=\frac{25}{18}\)
Vậy Bmax = 25/36 <=> b = 25/18
a,\(A=8a-8a^2+3\)
\(=-8\left(a^2-a\right)+3\)
\(=-8\left(a^2-2a\frac{1}{2}+\frac{1}{4}-\frac{1}{4}\right)+3\)
\(=-8\left[\left(a-\frac{1}{2}\right)^2-\frac{1}{4}\right]+3\)
\(=-8\left(a-\frac{1}{2}\right)^2+2+3\)
\(=-8\left(a-\frac{1}{2}\right)^2+5\le5\forall a\)
Dấu"=" xảy ra khi \(\left(a-\frac{1}{2}\right)^2=0\Rightarrow a=\frac{1}{2}\)
Vậy \(Max_A=5\)khi\(a=\frac{1}{2}\)
bài 2:
b,\(D=d^2+10e^2-6de-10e+26\)
\(=d^2-23de+\left(3e\right)^2+e^2-2.5e+5^2+1\)
\(=\left(d-3e\right)^2+\left(e-5\right)^2+1\ge1\forall d,e\)
Dấu"=" xảy ra khi\(\orbr{\begin{cases}\left(d-3e\right)^2=0\\\left(e-5\right)^2=0\end{cases}\Rightarrow\orbr{\begin{cases}d=15\\e=5\end{cases}}}\)
vậy \(D_{min}=1\)khi \(d=15;e=5\)
c,:\(E=4x^4+12x^2+11\)
\(=\left(2x^2\right)^2+2.2x^2.3+3^2+2\)
\(=\left(2x^2+3\right)^2+2\ge2\forall x\)
còn 1 đoạn nx bạn tự lm tiếp,lm giống như D
2. a. \(C=\frac{1}{16}c^2-9c+10=\frac{1}{16}\left(x-72\right)^2-314\)
Vì \(\left(x-72\right)^2\ge0\forall x\)\(\Rightarrow\frac{1}{16}\left(x-72\right)^2-314\ge-314\)
Dấu "=" xảy ra \(\Leftrightarrow\frac{1}{16}\left(x-72\right)^2=0\Leftrightarrow x-72=0\Leftrightarrow x=72\)
Vậy Cmin = - 314 <=> x = 72
b. \(D=d^2+10e^2-6de-10e+26=\left(d^2-6de+9e^2\right)+\left(e^2-10e+25\right)+1\)
\(=\left(d-3e\right)^2+\left(e-5\right)^2+1\)
Vì \(\left(d-3e\right)^2\ge0;\left(e-5\right)^2\ge0\forall d;e\)\(\Rightarrow\left(d-3e\right)^2+\left(e-5\right)^2+1\ge1\)
Dấu "=" xảy ra \(\Leftrightarrow\orbr{\begin{cases}\left(d-3e\right)^2=0\\\left(e-5\right)^2=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}d-3e=0\\e=5\end{cases}}\Leftrightarrow\orbr{\begin{cases}d=15\\e=5\end{cases}}\)
Vậy Dmin = 1 <=> d = 15 ; e = 5
c. \(E=4x^4+12x^2+11=\left(2x^2+3\right)^2+2\)
Vì \(\left(2x^2+3\right)^2\ge0\forall x\)\(\Rightarrow\left(2x^2+3\right)^2+2\ge2\)
Dấu "=" xảy ra \(\Leftrightarrow\left(2x^2+3\right)^2=0\Leftrightarrow2x^2+3=0\Leftrightarrow x^2=-\frac{3}{2}\left(vo-ly\right)\)
Không thể xảy ra dấu "=" trong th này
Vậy để Emin thì \(\left(2x^2+3\right)^2_{min}=\left(3^2\right)=9\Leftrightarrow2x^2=0\Leftrightarrow x=0\)
Vậy Emin = 9 + 2 = 11 <=> x = 0
tìm gtnn các biểu thức s a)x2+2x+2020
b)m2+4m-1
c)m2+m
d)x-2căn x+10
e)4x-8 căn x +2020
\(a,=x^2+2x+1+2019=\left(x+1\right)^2+2019\ge2019\) dấu"=" xảy ra<=>x=-1
b,\(=m^2+2.2m+4-5=\left(m+2\right)^2-5\ge-5\) dấu"=" xảy ra<=>m=-2
c, \(=x-2\sqrt{x}+10=x-2\sqrt{x}+1+9=\left(\sqrt{x}-1\right)^2+9\ge9\)
dấu"=" xảy ra<=>x=1
b, \(4x-8\sqrt{x}+2020=4x-2.2.2\sqrt{x}+4+2016=\left(2\sqrt{x}-2\right)^2+2016\ge2016\)
dấu"=" xảy ra<=>x=1
Đúng 1
Bình luận (0)
a) Ta có: \(x^2+2x+2020\)
\(=x^2+2x+1+2019\)
\(=\left(x+1\right)^2+2019\ge2019\forall x\)
Dấu '=' xảy ra khi x=-1
b) Ta có: \(m^2+4m-1\)
\(=m^2+4m+4-5\)
\(=\left(m+2\right)^2-5\ge-5\forall m\)
Dấu '=' xảy ra khi m=-2
c) Ta có: \(m^2+m\)
\(=m^2+2\cdot m\cdot\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{1}{4}\)
\(=\left(m+\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\forall m\)
Dấu '=' xảy ra khi \(m=-\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
Bài 8: tìm x
a) x + 10 = 20
b) 2 . x + 15 = 35
c) 3 ⋅ ( x + 2 ) = 15
d) 10 . x + 15 . 11 = 20 . 10
e) 4 . ( x + 2 ) = 3 . 4
f) 33 x + 135 = 26 . 9
g) 2 . x + 15 + 16 + 17 = 100
h) 2 . (x + 9 + 10 + 11) = 4 . 12 . 25
a) x + 10 = 20
<=> x = 20 - 10 = 10
Vậy x = 10
b) 2x + 15 = 35
<=> 2x = 35 - 15 = 20
<=> x = 10
Vậy x = 10
c) 3(x + 2) = 15
<=> x + 2 = 15 : 3 = 5
<=> x = 5 - 2 = 3
Vậy x = 3
d) 10x + 15.11 = 20.10
<=> 10x + 165 = 200
<=> 10x = 200 - 165 = 35
<=> x = 35 : 10 = 3,5
Vậy x = 3,5
e) 4(x + 2) = 3.4
<=> x + 2 = 3
<=> x = 3 - 2 = 1
Vậy x = 1
f) 33x + 135 = 26.9
<=> 33x + 135 = 234
<=> 33x = 234 - 135 = 99
<=> x = 99 : 33 = 3
Vậy x = 3
g) 2x + 15 + 16 + 17 = 100
<=> 2x + 48 = 100
<=> 2x = 100 - 48 = 52
<=> x = 52 : 2 = 26
Vậy x = 26
h) 2(x + 9 + 10 + 11) = 4.12.5
<=> x + 30 = 120
<=> x = 120 - 30 = 90
Vậy x = 90
Đúng 2
Bình luận (2)
c) 2x = 5y và x – y = 15 d)x/2 = y/5 và xy = 10
e)x-1/2 = y-2/3 = z-3/4 và 2x +3y - z = 50
giúp mk vs ạ
c) Ta có:
2x=5y=>x/5=y/2
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
x/5=y/2=x-y/5-2=15/3=5
=> x=5.5=25; y=5.2=10
d)Đặt x/2=y/5=k
=> x=2k; y=5k=> xy=2k.5k=10k^2=10=> k^2=1=>k=\(\pm\)1
Với k=1=>x=2; y=5
Với k=-1=>x=-2; y=-5
Đúng 0
Bình luận (0)