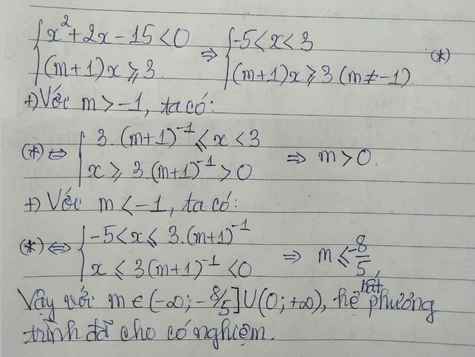 Mọi người giải hộ mình câu này với ạ mình cần gấp
Mọi người giải hộ mình câu này với ạ mình cần gấp
NA
Những câu hỏi liên quan
Mọi người giúp mình giải mấy câu này với ạ! Mình cần gấp trước 10h tối ạ!
1.
\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=0\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=0\)
\(\Leftrightarrow x-\dfrac{\pi}{4}=k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+k\pi\)
2.
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x+\dfrac{\pi}{4}=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
Đúng 2
Bình luận (0)
3.
\(\Leftrightarrow\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x=\dfrac{5}{8}\)
\(\Leftrightarrow1-\dfrac{1}{2}sin^22x=\dfrac{5}{8}\)
\(\Leftrightarrow1-\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{2}cos4x\right)=\dfrac{5}{8}\)
\(\Leftrightarrow\dfrac{3}{4}+\dfrac{1}{4}cos4x=\dfrac{5}{8}\)
\(\Leftrightarrow cos4x=-\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=\dfrac{2\pi}{3}+k2\pi\\4x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+\dfrac{k\pi}{2}\\x=-\dfrac{\pi}{6}+\dfrac{k\pi}{2}\end{matrix}\right.\)
Đúng 3
Bình luận (0)
4.
\(\Leftrightarrow\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)=\dfrac{1}{4}\)
\(\Leftrightarrow1-\dfrac{3}{4}sin^22x=\dfrac{1}{4}\)
\(\Leftrightarrow1-\dfrac{3}{4}\left(\dfrac{1}{2}-\dfrac{1}{2}cos4x\right)=\dfrac{1}{4}\)
\(\Leftrightarrow cos4x=-1\)
\(\Leftrightarrow4x=\pi+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giải hộ mình câu c bài này với ạ, mình cảm ơn nhiều nhiều ^^
Mình đag cần gấp, làm nhanh hộ mình với ạ <3

ext-9bosssssssssssssssss


Phiền mọi người giúp mình bài này với ạ, mọi người giải thì ghi chi tiết giúp mình ạ.
Phiền mọi người giúp, bài này mình đang cần gấp ạ
\(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{24\cdot12}{24+12}=8\Omega\)
\(I=\dfrac{U}{R}=\dfrac{12}{8}=1,5A\)
\(P=\dfrac{U^2}{R}=\dfrac{12^2}{8}=18W\)
\(Q_{tỏa1}=A_1=U_1\cdot I_1\cdot t=12\cdot\dfrac{12}{24}\cdot1\cdot3600=21600J\)
\(Q_{tỏa2}=A_2=U_2\cdot I_2\cdot t=12\cdot\dfrac{12}{12}\cdot1\cdot3600=43200J\)
Đúng 1
Bình luận (1)
mọi người ai giải hộ em câu này với em đang cần gấp câu này em cảm ơn ạ!

a: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp
Đúng 0
Bình luận (0)
Giải hộ mình câu c bài này với ạ, mình cảm ơn nhiều nhiều ^^
Mình đag cần gấp lắm ạ, làm nhanh hộ mình với <3
Cảm ơn lần nữa

1) Vì x=25 thỏa mãn ĐKXĐ nên Thay x=25 vào biểu thức \(A=\dfrac{\sqrt{x}-2}{x+1}\), ta được:
\(A=\dfrac{\sqrt{25}-2}{25+1}=\dfrac{5-2}{25+1}=\dfrac{3}{26}\)
Vậy: Khi x=25 thì \(A=\dfrac{3}{26}\)
2) Ta có: \(B=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}+\dfrac{2x+8\sqrt{x}-6}{x-\sqrt{x}-2}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-5\sqrt{x}+6+2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3x+3\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}-2}\)
Đúng 0
Bình luận (0)
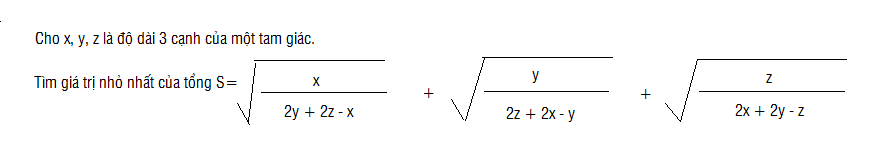
Mọi người giải hộ mình với ạ, đang cần gấp
Áp dụng BĐT cauchy, ta có:
\(\sqrt{\left(2y+2z-x\right)\cdot3x}\le\dfrac{2z+2y-x+3x}{2}=\dfrac{2\left(x+y+z\right)}{2}=x+y+z\\ \Leftrightarrow\sqrt{2y+2z-x}\le\dfrac{x+y+z}{\sqrt{3x}}\\ \Leftrightarrow\sqrt{\dfrac{x}{2y+2z-x}}\ge\dfrac{\sqrt{x}}{\dfrac{x+y+z}{\sqrt{3x}}}=\dfrac{x\sqrt{3}}{x+y+z}\)
\(\Leftrightarrow S=\sum\sqrt{\dfrac{x}{2y+2z-x}}\ge\sqrt{3}\left(\dfrac{x}{x+y+z}+\dfrac{y}{x+y+z}+\dfrac{z}{x+y+z}\right)\\ \Leftrightarrow S\ge\sqrt{3}\cdot\dfrac{x+y+z}{x+y+z}=\sqrt{3}\)
Dấu \("="\Leftrightarrow x=y=z\) hay tam giác đều
Đúng 2
Bình luận (0)
Mọi người giúp mình câu này với ạ. Mình đang cần gấp ạ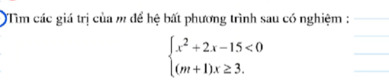
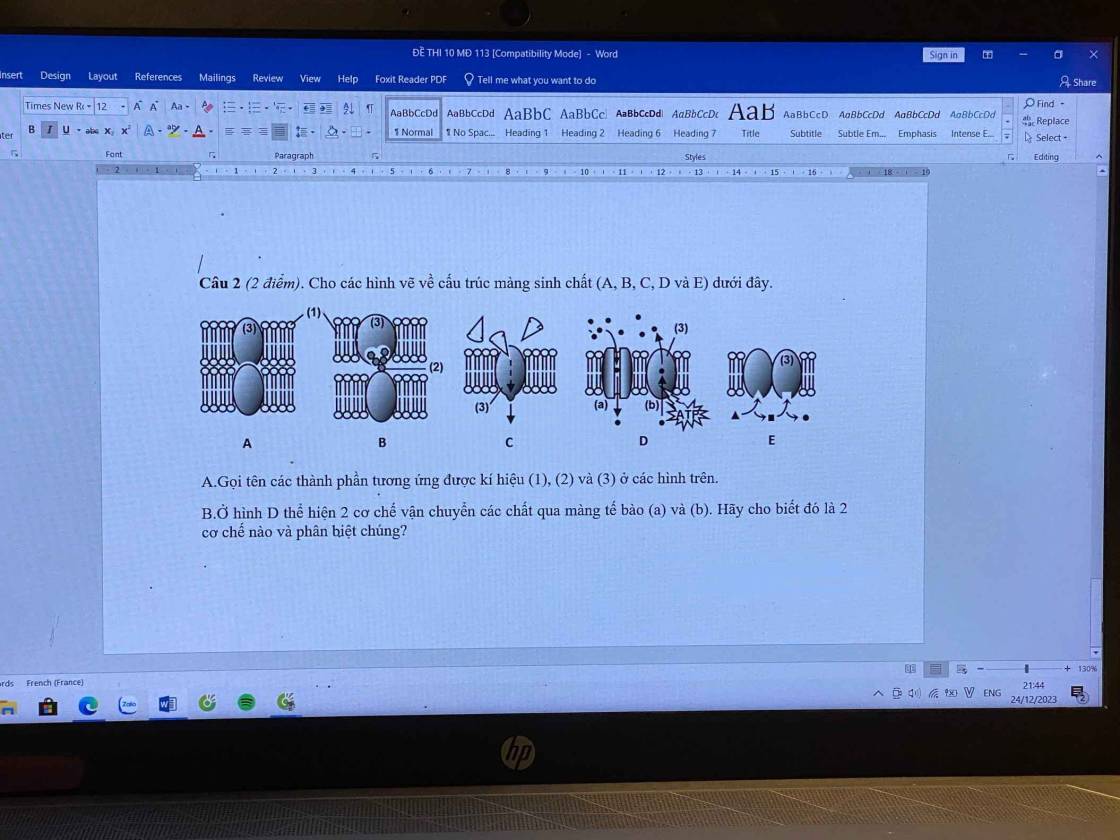
mọi người giúp mình câu này với ạ. mình đang cần gấp
Mọi người giúp mình câu này với ạ! Mình đang cần gấp lắm!!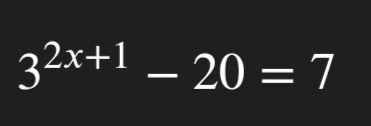
3²ˣ⁺¹ - 20 = 7
3²ˣ⁺¹ = 7 + 20
3²ˣ⁺¹ = 27
3²ˣ⁺¹ = 3³
2x + 1 = 3
2x = 3 - 1
2x = 2
x = 2 : 2
x = 1
Đúng 0
Bình luận (0)