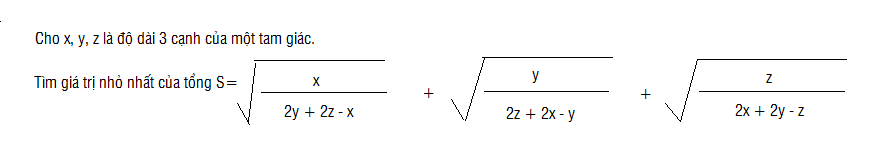Áp dụng BĐT cauchy, ta có:
\(\sqrt{\left(2y+2z-x\right)\cdot3x}\le\dfrac{2z+2y-x+3x}{2}=\dfrac{2\left(x+y+z\right)}{2}=x+y+z\\ \Leftrightarrow\sqrt{2y+2z-x}\le\dfrac{x+y+z}{\sqrt{3x}}\\ \Leftrightarrow\sqrt{\dfrac{x}{2y+2z-x}}\ge\dfrac{\sqrt{x}}{\dfrac{x+y+z}{\sqrt{3x}}}=\dfrac{x\sqrt{3}}{x+y+z}\)
\(\Leftrightarrow S=\sum\sqrt{\dfrac{x}{2y+2z-x}}\ge\sqrt{3}\left(\dfrac{x}{x+y+z}+\dfrac{y}{x+y+z}+\dfrac{z}{x+y+z}\right)\\ \Leftrightarrow S\ge\sqrt{3}\cdot\dfrac{x+y+z}{x+y+z}=\sqrt{3}\)
Dấu \("="\Leftrightarrow x=y=z\) hay tam giác đều