y=2cotx-1/3cosx
Câu 1)
a) 2cos2x-3cosx+1=0
b)2sin2x+√2 sin4x=0
C)sin2x/2-2cosx/2+2=0
d)tanx-2cotx+1=0
a/
\(\Leftrightarrow\left(cosx-1\right)\left(2cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pm\frac{\pi}{3}+k2\pi\end{matrix}\right.\)
b \(\Leftrightarrow2sin2x+2\sqrt{2}sin2x.cos2x=0\)
\(\Leftrightarrow2sin2x\left(1+\sqrt{2}cos2x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=0\\cos2x=-\frac{\sqrt{2}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=k\pi\\2x=\pm\frac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{k\pi}{2}\\x=\pm\frac{3\pi}{8}+k\pi\end{matrix}\right.\)
c/
\(\Leftrightarrow1-cos^2\frac{x}{2}-2cos\frac{x}{2}+2=0\)
\(\Leftrightarrow cos^2\frac{x}{2}+2cos\frac{x}{2}-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos\frac{x}{2}=1\\cos\frac{x}{2}=-3< -1\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow\frac{x}{2}=k2\pi\)
\(\Leftrightarrow x=k4\pi\)
d/ ĐKXĐ: ...
\(\Leftrightarrow tanx-\frac{2}{tanx}+1=0\)
\(\Leftrightarrow tan^2x+tanx-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=1\\tanx=-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+k\pi\\x=arctan\left(-2\right)+k\pi\end{matrix}\right.\)
Tìm tất cả các giá trị của m để hàm số y = 8cotx + (m - 3).2cotx + 3m - 2 (1) đồng biến trên \([\dfrac{\pi}{4};\pi)\)
Đặt \(2^{cotx}=t\Rightarrow t\in(-\infty;1]\)
Để ý rằng \(cotx\) nghịch biến trên khoảng đã cho nên \(f\left(x\right)\) đồng biến \(\Leftrightarrow f\left(t\right)=t^3+\left(m-3\right)t+3m-2\) nghịch biến trên \((-\infty;1]\)
Quy về 1 bài toán đồng biến - nghịch biến bình thường của hàm bậc 3
Ủa, ngáo rồi, đặt \(2^{cotx}=t\) chứ có phải \(cotx=t\) đâu, vậy \(t\in(0;2]\) mới đúng (cách làm vẫn y như trên, chỉ khác khoảng của t)
Tìm m để hàm số y = 2 cot x + 1 cot x + m đồng biến trên π 4 ; π 2 ?
A. m ∈ − ∞ ; − 2
B. m ∈ − ∞ ; − 1 ∪ 0 ; 1 2
C. m ∈ − 2 ; + ∞
D. m ∈ 1 2 ; + ∞
Đáp án B
Xét hàm số
y = 2 cot x + 1 cot x + m → t = cot x y = 2 t + 1 t + m ⇒ y t ' = t ' . 2 m − 1 t + m 2
Để hàm số đã cho đồng biến trên
π 4 ; π 2 ⇔ y t ' > 0 , ∀ x ∈ 0 ; 1 ⇔ t ' . 2 m − 1 t + m 2 > 0 , ∀ x ∈ 0 ; 1
Mà
t ' < 0 , ∀ x ∈ 0 ; 1 ⇒ 2 m − 1 t + m 2 < 0 ; ∀ x ∈ 0 ; 1 ⇔ 2 m − 1 < 0 t = − m ∉ 0 ; 1 ⇔ m < 1 2 − m ≥ 1 − m ≤ 0 ⇔ m ≤ − 1 0 ≤ m < 1 2
(/2tanx-1/+/2cotx-1/=2?
/2tanx -1/+/2cotx-1/=2?
Tìm TXĐ của hàm số
y=\(\dfrac{cotx+3}{cosx}\)
y=\(\dfrac{2x}{3cosx-1}\)
Hàm số \(y=\dfrac{cotx+3}{cosx}\) xác định khi:
\(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne k\pi\\x\ne\dfrac{\pi}{2}+k\pi\end{matrix}\right.\Leftrightarrow x\ne\dfrac{k\pi}{2}\)
Hàm số \(\dfrac{2x}{3cosx-1}\) xác định khi:
\(3cosx-1\ne0\Leftrightarrow cosx\ne\dfrac{1}{3}\Leftrightarrow x\ne\pm arccos\left(\dfrac{1}{3}\right)+k2\pi\)
Giá trị của m để hàm số y = c o t x - 2 c o t x - m nghịch biến trên π 4 ; π 2 là
A. m>2
B. 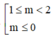
C. 1 ≤ m<2
D. m ≤ 0
Đáp án B
Phương pháp giải: Tính đạo hàm, áp dụng điều kiện để hàm số nghịch biến trên khoảng
Lời giải: Ta có
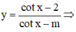
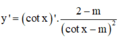
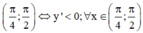 (*)
(*)
Mà 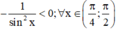 suy ra (*)
suy ra (*) 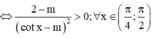
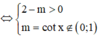
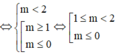
Vậy 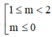 là giá trị cần tìm
là giá trị cần tìm
tìm nguyên hàm của hàm số y=x^(2)-3cosx+(1)/(x)
Tìm GTLN,GTNN của hàm số:
a, \(y=3cosx-1\)
b, \(y=5+2sinx\)
c,\(y=\sqrt{3+cos2x}\)
d,\(y=\sqrt{5sinx-1}+2\)
a.\(-1\le cosx\le1\Rightarrow-4\le y=3cosx-1\le2\)
b.-1 \(\le sinx\le1\)\(\Rightarrow3\le y=5+2sinx\le7\)
c.\(\sqrt{3-1}\le\sqrt{3+cos2x}\le\sqrt{3+1}\Rightarrow\sqrt{2}\le y\le2\)
d.\(y=\sqrt{5sinx-1}+2\le\sqrt{5.1-1}+2=4\)
\(y=\sqrt{5sinx-1}+2\ge2\) . " = " \(\Leftrightarrow sinx=\dfrac{1}{5}\Leftrightarrow\left[{}\begin{matrix}x=arcsin\left(\dfrac{1}{5}\right)+2k\pi\\x=\pi-arcsin\left(\dfrac{1}{5}\right)+2k\pi\end{matrix}\right.\) ( k thuộc Z )