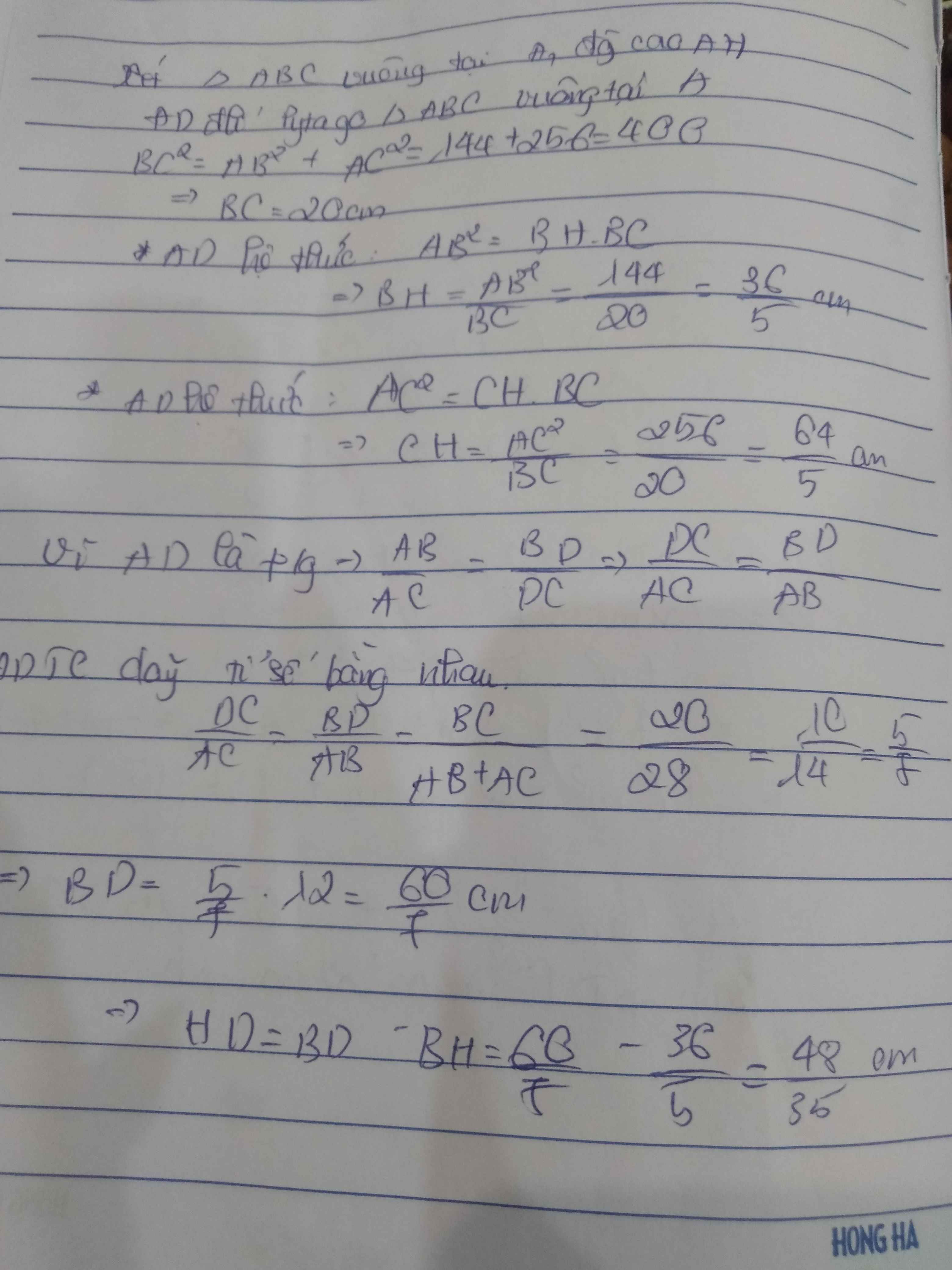Cho ∆ABC vuông tại A, AB = 12cm, AC = 16cm, phân giác AD, đường cao AH. Tính HD, HB, HC.
NS
Những câu hỏi liên quan
Cho ∆ABC vuông tại A , AB = 12cm , AC = 16cm , phân giác AD , đường cao AH . Tính HB , HC , HD
Lời giải:
Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}=20$ (cm)
Áp dụng tính chất tia phân giác:
$\frac{BD}{DC}=\frac{AB}{AC}=\frac{12}{16}=\frac{3}{4}$
Mà: $BD+DC=BC=20$
$\Rightarrow BD=20:(3+4).3=\frac{60}{7}$ (cm)
Theo hệ thức lượng của tam giác vuông:
$HB=\frac{AB^2}{BC}=\frac{12^2}{20}=7,2$ (cm)
$CH=BC-HB=20-7,2=12,8$ (cm)
$HD=BD-BH=\frac{60}{7}-7,2=\frac{48}{35}$ (cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A . Biết AB = 12cm , AC = 16cm,phân giác AD , đường cao AH . Tính HD , HB , HC.
Ta có: BC^2 = AB^2 + AC^2
= 12^2 + 16^2 = 400
=> BC = √400 = 20 (cm)
Δ ABC vuông có đường cao AH:
=> AB^2 = BH.BC
=> BH = AB^2/BC = 12^2/20 = 7.2 (cm)
=> CH = 20 - 7.2 = 12.8 (cm)
Ta có: AD là phân giác
=> BD/CD = AB/AC
=>( BD + CD)/CD = (AB + AC)/AC
=> 20/CD = 28/16
=> CD = 80/7
=> HD = CH - CD
= 12.8 - (80/7)
= 48/35 (cm)
(HC tự tính nha)
Đúng 5
Bình luận (1)
cho tam giác ABC vuông tại A , AB = 12cm , AC = 16cm , tia phân giác AD , đường cao Ah , Tinh HD , HB , HC
tự vẽ hình..
\(BC=\sqrt{AC^2+AB^2}=\sqrt{12^2+16^2}=20cm\)( Định lý pitago cho tam giác vuông ABC)
\(\Rightarrow BH=\frac{AB^2}{BC}=\frac{12^2}{20}=7,2cm\)( Áp dụng hệ thức lương cho tam giác vuông ABC)
\(HC=BC-HB=20-7,2=12,8cm\)
Đúng 0
Bình luận (0)
Áp dụng tính chất tia phân giác: \(\frac{BD}{AB}=\frac{CD}{AC}=\frac{BD+CD}{AB+AC}=\frac{BC}{12+16}=\frac{20}{12+16}=\frac{5}{7}\)
\(\Rightarrow BD=\frac{AB.5}{7}=\frac{12.5}{7}\approx8,571\)( chả biết ý này có đ ko nx)
Đúng 0
Bình luận (1)
1. Cho ∆ABC biết BC = 7.5cm, AC = 4.5cm, AB = 6cm.
a) ∆ABC là tam giác gì? Tính đường cao AH của ∆ABC.
b) Tính độ dài các cạnh BH, HC.
2. Cho ∆ABC vuông tại A, AB = 12cm, AC = 16cm, phân giác AD, đường cao AH. Tính HD, HB, HC.
1)
a) Xét ΔABC có
\(BC^2=AC^2+AB^2\left(7.5^2=4.5^2+6^2\right)\)
nên ΔABC vuông tại A(Định lí Pytago đảo)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A, ta được:
\(AB\cdot AC=AH\cdot BC\)
\(\Leftrightarrow AH=\dfrac{AB\cdot AC}{BC}=\dfrac{4.5\cdot6}{7.5}=\dfrac{27}{7.5}=3.6\left(cm\right)\)
Vậy: AH=3,6cm
b) Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AC^2=AH^2+CH^2\)
\(\Leftrightarrow CH^2=4.5^2-3.6^2=7.29\)
hay CH=2,7(cm)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên BH=BC-CH=7,5-2,7=4,8(cm)
Vậy: BH=4,8cm; CH=2,7cm
Đúng 3
Bình luận (0)
1.a)Ta có:7,52=4,52+62 nên theo định lí Py-ta-go
=>\(\Delta ABC\) vuông tại A
Ta có: AB.AC=BC.AH
=> \(AH=\dfrac{AC.AB}{BC}=\dfrac{4,5.6}{7,5}=3.6\) (cm)
Đúng 2
Bình luận (0)
b)Ta có:AB2=BC.BH
\(\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{7,5}=4,8\) (cm)
Ta có:BH+CH=BC
=>CH=BC-BH=7,5-4,8=2,7 (cm)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
cho tam giác ABC vuông tại A, có AB = 12cm, AC=16cm, phân giác AD,đường cao AH. tính đọ dài các đoạn HB, HC, HD
Ta có: BC2 = AB2 + AC2 \(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}=20cm\)
\(AB^2=HB.BC\Rightarrow HB=\frac{AB^2}{BC}=\frac{12^2}{20}=\frac{36}{5}=7,2cm\)
\(AC^2=HC.BC\Rightarrow HC=\frac{AC^2}{BC}=\frac{16^2}{20}=\frac{64}{5}=12,8cm\)
Vì AD là phân giác góc BAC nên ta có :
\(\frac{DB}{DC}=\frac{AB}{AC}=\frac{12}{16}=\frac{3}{4}\Rightarrow DC=\frac{4}{7}BC=\frac{4}{7}.20=\frac{80}{7}cm\)
=> HD = BC - (HB + DC) \(=20-\left(7,2+\frac{80}{7}\right)=\frac{48}{35}cm\)
Vậy HB = 7,2cm ; HC = 12,8cm ; HD = 48/35cm
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A, AB = 9cm, AC = 12cm, phân giác AD, đường cao AH. Tính HB,HC,HD
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=9^2+12^2=225\)
hay BC=15cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=5,4cm\\CH=9,6cm\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A . Biết AB = 12cm , AC = 16cm,phân giác AD , đường cao AH . Tính HD , HB , HC.
Xét tam giác ABC vuông tại A, đường cao AH
Áp dụng định lí Pytago tam giác ABC vuông tại A
\(BC^2=AB^2+AC^2=144+256=400\Rightarrow BC=20\)cm
* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{144}{20}=\frac{36}{5}\)cm
* Áp dụng hệ thức : \(AC^2=CH.BC\Rightarrow CH=\frac{AC^2}{BC}=\frac{256}{20}=12,8\)cm
Vì AD là đường pg nên \(\frac{AB}{AC}=\frac{BD}{DC}\Rightarrow\frac{DC}{AC}=\frac{BD}{AB}\)
Áp dụng tunhs chất dãy tỉ số bằng nhau
\(\frac{DC}{AC}=\frac{BD}{AB}=\frac{BC}{AB+AC}=\frac{20}{28}=\frac{5}{7}\)
\(\Rightarrow BD=\frac{5}{7}.AB=\frac{5}{7}.12=\frac{60}{7}\)cm
=> \(HD=BD-BH=\frac{60}{7}-\frac{36}{5}=\frac{48}{35}\)cm
Cho tam giác ABC vuông tại A , AB = 12cm, AC = 16cm, phân giác AD, đường cao AH. Tính HD , HB
( vẽ hình nữa nha )
Ta có: BC^2 = AB^2 + AC^2
= 12^2 + 16^2 = 400
=> BC = √400 = 20 (cm)
Δ ABC vuông có đường cao AH:
=> AB^2 = BH.BC
=> BH = AB^2/BC = 12^2/20 = 7.2 (cm)
=> CH = 20 - 7.2 = 12.8 (cm)
Ta có: AD là phân giác
=> BD/CD = AB/AC
=>( BD + CD)/CD = (AB + AC)/AC
=> 20/CD = 28/16
=> CD = 80/7
=> HD = CH - CD
= 12.8 - (80/7)
= 48/35 (cm)
Đúng 0
Bình luận (0)
HB bạn kia tính đúng rồi, mình chỉ tính lại HD thôi nhá
AH= \(\sqrt{12^2-7,2^2}\)= 9,6
cosB = \(\frac{BH}{AB}\)= \(\frac{7,2}{12}\)= 0,6 => B = 59 độ
\(\widehat{BAH}\)= 180-90-59= 31 độ
\(\widehat{HAD}\)= 90 :2 -31 = 14 độ
tan14= \(\frac{HD}{AH}\)= \(\frac{HD}{9,6}\)= 0,22 (tan14=0,22)
=> HD= 2,112 cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông AC=16cm,AB=12cm,Phân giác AD, đường cao AH.Tính HB, HD, HC
\(BC=\sqrt{AB^2+AC^2}=20\left(cm\right)\left(pytago\right)\)
Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=\dfrac{144}{20}=7,2\left(cm\right)\\CH=\dfrac{AC^2}{BC}=\dfrac{256}{20}=12,8\left(cm\right)\end{matrix}\right.\)
Vì AD là phân giác nên \(\dfrac{AB}{AC}=\dfrac{BD}{DC}=\dfrac{12}{16}=\dfrac{3}{4}\Rightarrow BD=\dfrac{3}{4}DC\)
Mà \(BD+DC=BC=20\Leftrightarrow\dfrac{7}{4}DC=20\Leftrightarrow DC=\dfrac{80}{7}\left(cm\right)\)
\(\Leftrightarrow HD=CH-CD=12.8-\dfrac{80}{7}=\dfrac{48}{35}\left(cm\right)\)
Đúng 1
Bình luận (0)