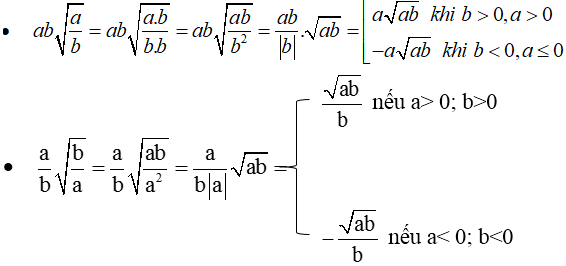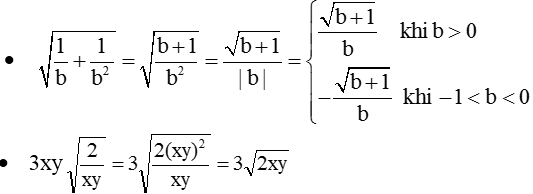B=3:(\(-\dfrac{3}{2}\))+\(\dfrac{1}{9}\).\(\sqrt{36}\)
VN
Những câu hỏi liên quan
Bài 49 (trang 29 SGK Toán 9 Tập 1)
Khử mẫu của biểu thức lấy căn
$ab\sqrt{\dfrac{a}{b}}$ ; $\dfrac{a}{b} \sqrt{\dfrac{b}{a}}$ ; $\sqrt{\dfrac{1}{b}+\dfrac{1}{b^{2}}}$ ; $\sqrt{\dfrac{9 a^{3}}{36 b}}$ ; $3 xy \sqrt{\dfrac{2}{x y}}$.
(Giả thiết các biểu thức có nghĩa).
(do xy > 0 (gt) nên đưa thừa số xy vào trong căn để khử mẫu)
#Học tốt!!!
\(ab\cdot\sqrt{\dfrac{a}{b}}=a\cdot\sqrt{ab}\)
\(\dfrac{a}{b}\cdot\sqrt{\dfrac{b}{a}}=\dfrac{\sqrt{a\cdot b}}{b}\)
\(\sqrt{\dfrac{1}{b}+\dfrac{1}{b^2}}=\dfrac{\sqrt{b+1}}{b}\)
\(\sqrt{\dfrac{9\cdot a^3}{36\cdot b}}=\dfrac{\sqrt{a^3\cdot b}}{2\cdot b}\)
\(3\cdot x\cdot y\cdot\sqrt{\dfrac{2}{x\cdot y}}=3\cdot\sqrt{2\cdot x\cdot y}\)
\(a\cdot b\cdot\sqrt{\dfrac{a}{b}}=a\cdot\sqrt{a\cdot b}\)
\(\dfrac{a}{b}\cdot\sqrt{\dfrac{b}{a}}=\dfrac{\sqrt{a\cdot b}}{b}\)
\(\sqrt{\dfrac{1}{b}+\dfrac{1}{b^2}}=\dfrac{\sqrt{b+1}}{b}\)
\(\sqrt{\dfrac{9\cdot a^3}{36\cdot b}}=\dfrac{\sqrt{a^3\cdot b}}{2\cdot b}\)
\(3\cdot x\cdot y\cdot\sqrt{\dfrac{2}{x\cdot y}}=3\cdot\sqrt{2\cdot x\cdot y}\)
Xem thêm câu trả lời
1. tính
a,sqrt{dfrac{1,44}{3,61}} ; b, sqrt{dfrac{0,25}{9}} ; c, sqrt{1dfrac{13}{36}}.sqrt{3dfrac{13}{36}}
d,sqrt{dfrac{1}{121}.3dfrac{6}{25}} ; e,sqrt{1dfrac{13}{36}.2dfrac{2}{49}.2dfrac{7}{9}} ; g,
2. Tính
a, dfrac{sqrt{245}}{sqrt{5}} ; b, dfrac{sqrt{3}}{sqrt{75}} ; c, dfrac{sqrt{10,8}}{sqrt{0,3}} ; d, dfrac{sqrt{6,5}}{sqrt{58,5}}
3. Tính.
a, sqrt{dfrac{...
Đọc tiếp
1. tính
a,\(\sqrt{\dfrac{1,44}{3,61}}\) ; b, \(\sqrt{\dfrac{0,25}{9}}\) ; c, \(\sqrt{1\dfrac{13}{36}}.\sqrt{3\dfrac{13}{36}}\)
d,\(\sqrt{\dfrac{1}{121}.3\dfrac{6}{25}}\) ; e,\(\sqrt{1\dfrac{13}{36}.2\dfrac{2}{49}.2\dfrac{7}{9}}\) ; g,
2. Tính
a, \(\dfrac{\sqrt{245}}{\sqrt{5}}\) ; b, \(\dfrac{\sqrt{3}}{\sqrt{75}}\) ; c, \(\dfrac{\sqrt{10,8}}{\sqrt{0,3}}\) ; d, \(\dfrac{\sqrt{6,5}}{\sqrt{58,5}}\)
3. Tính.
a, \(\sqrt{\dfrac{61^2-60^2}{81}}\) ; b, \(\sqrt{\dfrac{74^2-24^2}{121}}\)
4. Tìm số x không âm, biết:
a, 9 - 4 \(\sqrt{x}=1\) ; b, \(\sqrt{\dfrac{x}{5}}=4\) c, \(\sqrt{7x}< 9\)
Bài 1 :
Câu a : \(\sqrt{\dfrac{1,44}{3,61}}=\sqrt{\dfrac{144}{361}}=\dfrac{\sqrt{144}}{\sqrt{361}}=\dfrac{12}{19}\)
Câu b : \(\sqrt{\dfrac{0,25}{9}}=\sqrt{\dfrac{25}{900}}=\dfrac{\sqrt{25}}{\sqrt{900}}=\dfrac{5}{30}=\dfrac{1}{6}\)
Câu c : \(\sqrt{1\dfrac{13}{36}}.\sqrt{3\dfrac{13}{36}}=\sqrt{\dfrac{49}{36}}.\sqrt{\dfrac{121}{46}}=\dfrac{\sqrt{49}}{\sqrt{36}}.\dfrac{\sqrt{121}}{36}=\dfrac{7}{6}.\dfrac{11}{6}=\dfrac{77}{36}\)
Câu d : \(\sqrt{\dfrac{1}{121}.3\dfrac{6}{25}}=\sqrt{\dfrac{1}{121}.\dfrac{81}{25}}=\dfrac{1}{\sqrt{121}}.\dfrac{\sqrt{81}}{\sqrt{25}}=\dfrac{1}{11}.\dfrac{9}{5}=\dfrac{9}{55}\)
Câu e : \(\sqrt{1\dfrac{13}{36}.2\dfrac{2}{49}.2\dfrac{7}{9}}=\sqrt{\dfrac{49}{36}.\dfrac{100}{49}.\dfrac{25}{9}}=\dfrac{\sqrt{49}}{\sqrt{36}}.\dfrac{\sqrt{100}}{\sqrt{49}}.\dfrac{\sqrt{25}}{\sqrt{9}}=\dfrac{7}{6}.\dfrac{10}{7}.\dfrac{5}{3}=\dfrac{25}{9}\)
Đúng 1
Bình luận (0)
Bài 2 :
Câu a : \(\dfrac{\sqrt{245}}{\sqrt{5}}=\sqrt{\dfrac{245}{5}}=\sqrt{49}=7\)
Câu b : \(\dfrac{\sqrt{3}}{\sqrt{75}}=\sqrt{\dfrac{3}{75}}=\sqrt{\dfrac{1}{25}}=\dfrac{1}{5}\)
Câu c : \(\dfrac{\sqrt{10,8}}{\sqrt{0,3}}=\sqrt{\dfrac{10,8}{0,3}}=\sqrt{\dfrac{108}{3}}=\sqrt{36}=6\)
Câu d : \(\dfrac{\sqrt{6,5}}{\sqrt{58,5}}=\sqrt{\dfrac{6,5}{58,5}}=\sqrt{\dfrac{65}{585}}=\sqrt{\dfrac{1}{9}}=\dfrac{1}{3}\)
Đúng 0
Bình luận (0)
Bài 3 :
Câu a : \(\sqrt{\dfrac{61^2-60^2}{81}}=\sqrt{\dfrac{\left(61-60\right)\left(61+60\right)}{81}}=\sqrt{\dfrac{121}{81}}=\dfrac{\sqrt{121}}{81}=\dfrac{11}{9}\)
Câu b : \(\sqrt{\dfrac{74^2-24^2}{121}}=\sqrt{\dfrac{\left(74+24\right)\left(74-24\right)}{121}}=\sqrt{\dfrac{98.50}{121}}=\dfrac{\sqrt{4900}}{\sqrt{121}}=\dfrac{70}{11}\)
Bài 4 :
Câu a : \(9-4\sqrt{x}=1\Leftrightarrow4\sqrt{x}=8\Leftrightarrow\sqrt{x}=2\Leftrightarrow x=4\)
Câu b : \(\sqrt{\dfrac{x}{5}}=4\Leftrightarrow\dfrac{x}{5}=16\Leftrightarrow x=80\)
Câu c : \(\sqrt{7x}< 9\Leftrightarrow7x< 81\Leftrightarrow x< \dfrac{81}{7}\)
Đúng 0
Bình luận (0)
1. rút gọn bt
Q= \(\left(\dfrac{3+\sqrt{x}}{3-\sqrt{x}}-\dfrac{3-\sqrt{x}}{3+\sqrt{x}}-\dfrac{36}{x-9}\right):\dfrac{\sqrt{x}-5}{3\sqrt{x}-x}\)
b, tìm để Q<0
Tính
a) \(2\sqrt{\dfrac{25}{16}}-3\sqrt{\dfrac{49}{36}}+4\sqrt{\dfrac{81}{64}}\)
b) \(\left(3\sqrt{2}\right)^2-\left(4\sqrt{\dfrac{1}{2}}\right)^2+\dfrac{1}{16}.\left(\sqrt{\dfrac{3}{4}}\right)^2\)
c) \(\dfrac{2}{3}\sqrt{\dfrac{81}{16}}-\dfrac{3}{4}\sqrt{\dfrac{64}{9}}+\dfrac{7}{5}.\sqrt{\dfrac{25}{196}}\)
a: \(=2\cdot\dfrac{5}{4}-3\cdot\dfrac{7}{6}+4\cdot\dfrac{9}{8}=\dfrac{5}{2}-\dfrac{7}{2}+\dfrac{9}{2}=\dfrac{7}{2}\)
b: \(=18-16\cdot\dfrac{1}{2}+\dfrac{1}{16}\cdot\dfrac{3}{4}\)
=10+3/64
=643/64
c: \(=\dfrac{2}{3}\cdot\dfrac{9}{4}-\dfrac{3}{4}\cdot\dfrac{8}{3}+\dfrac{7}{5}\cdot\dfrac{5}{14}=\dfrac{3}{2}-2+\dfrac{1}{2}=2-2=0\)
Đúng 0
Bình luận (0)
B = \(\dfrac{\sqrt{x}+3}{\sqrt{x}-3}+\dfrac{\sqrt{x}-3}{\sqrt{x}+3}-\dfrac{36}{x-9}\)
RÚT GỌN B
\(B=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}+\dfrac{\sqrt{x}-3}{\sqrt{x}+3}-\dfrac{36}{x-9}\)
\(=\dfrac{\left(\sqrt{x}+3\right)^2+\left(\sqrt{x}-3\right)^2-36}{x-9}\)
\(=\dfrac{x+6\sqrt{x}+9+x-6\sqrt{x}+9-36}{x-9}\)
\(=\dfrac{2x-18}{x-9}=\dfrac{2\left(x-9\right)}{x-9}=2\)
Đúng 0
Bình luận (0)
ĐKXĐ : \(x\ge0;x\ne9\)
Ta có : \(B=\dfrac{\left(\sqrt{x}+3\right)^2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}+\dfrac{\left(\sqrt{x}-3\right)^2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{36}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(B=\dfrac{x+6\sqrt{x}+9+x-6\sqrt{x}+9-36}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{2x-18}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{2\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=2\)
Đúng 0
Bình luận (0)
\(\dfrac{\sqrt{x}+3}{\sqrt{x}-3}-\dfrac{\sqrt{x}-3}{\sqrt{x}+3}-\dfrac{36}{x-9}\)
Chứng minh B= \(\dfrac{12}{\sqrt{x}+3}\)
\(B=\dfrac{x+6\sqrt{x}+9-x+6\sqrt{x}-9-36}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{12\sqrt{x}-36}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{12\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{12}{\sqrt{x}+3}\)
Đúng 0
Bình luận (0)
tính giá trị biểu thức saua) A2^{dfrac{1}{3}}.2^{dfrac{2}{3}}b) B36^{dfrac{3}{2}}c) C36^{dfrac{3}{2}}.left(dfrac{1}{6}right)^2d) Dsqrt{81}.left(dfrac{1}{3}right)^2e) Eleft(3+2sqrt{2}right)^{50}.left(3-2sqrt{2}right)^{50}f) F120^{sqrt{5}+1}.120^{3-sqrt{5}}g) Gleft(3+2sqrt{2}right)^{2019}.left(3sqrt{2}-4right)^{2018}
Đọc tiếp
tính giá trị biểu thức sau
a) \(A=2^{\dfrac{1}{3}}.2^{\dfrac{2}{3}}\)
b) \(B=36^{\dfrac{3}{2}}\)
c) \(C=36^{\dfrac{3}{2}}.\left(\dfrac{1}{6}\right)^2\)
d) \(D=\sqrt{81}.\left(\dfrac{1}{3}\right)^2\)
e) \(E=\left(3+2\sqrt{2}\right)^{50}.\left(3-2\sqrt{2}\right)^{50}\)
f) \(F=120^{\sqrt{5}+1}.120^{3-\sqrt{5}}\)
g) \(G=\left(3+2\sqrt{2}\right)^{2019}.\left(3\sqrt{2}-4\right)^{2018}\)
a: \(A=2^{\dfrac{1}{3}}\cdot2^{\dfrac{2}{3}}=2^{\dfrac{1}{3}+\dfrac{2}{3}}=2^{\dfrac{3}{3}}=2^1=2\)
b: \(B=36^{\dfrac{3}{2}}=\left(6^2\right)^{\dfrac{3}{2}}=6^{2\cdot\dfrac{3}{2}}=6^3=216\)
c: \(C=36^{\dfrac{3}{2}}\cdot\left(\dfrac{1}{6}\right)^2=\left(6^2\right)^{\dfrac{3}{2}}\cdot\dfrac{1}{6^2}=\dfrac{6^{2\cdot\dfrac{3}{2}}}{6^2}=\dfrac{6^3}{6^2}=6\)
d: \(D=\sqrt{81}\cdot\left(\dfrac{1}{3}\right)^2=9\cdot\dfrac{1}{3^2}=9\cdot\dfrac{1}{9}=1\)
e: \(E=\left(3+2\sqrt{2}\right)^{50}\cdot\left(3-2\sqrt{2}\right)^{50}\)
\(=\left[\left(3+2\sqrt{2}\right)\left(3-2\sqrt{2}\right)\right]^{50}\)
\(=\left(9-8\right)^{50}=1^{50}=1\)
f: \(F=120^{\sqrt{5}+1}\cdot120^{3-\sqrt{5}}\)
\(=120^{\sqrt{5}+1+3-\sqrt{5}}=120^4\)
g: \(G=\left(3+2\sqrt{2}\right)^{2019}\cdot\left(3\sqrt{2}-4\right)^{2018}\)
\(=\left(3+2\sqrt{2}\right)^{2018}\cdot\left(3\sqrt{2}-4\right)^{2018}\cdot\left(3+2\sqrt{2}\right)\)
\(=\left[\left(3+2\sqrt{2}\right)\left(3\sqrt{2}-4\right)\right]^{2018}\left(3+2\sqrt{2}\right)\)
\(=\left(9\sqrt{2}-12+12-8\sqrt{2}\right)^{2018}\cdot\left(3+2\sqrt{2}\right)\)
\(=\left(\sqrt{2}\right)^{2018}\cdot\left(3+2\sqrt{2}\right)=2^{\dfrac{1}{2}\cdot2018}\cdot\left(3+2\sqrt{2}\right)\)
\(=2^{1009}\cdot\left(3+2\sqrt{2}\right)\)
Đúng 2
Bình luận (0)
Đề bài: ax,y,z 0 và sqrt{x}+sqrt{y}+sqrt{z}1. Tìm Min P dfrac{x^3}{y+z}+dfrac{y^3}{z+x}+dfrac{z^3}{x+y}.
ĐÁP ÁN:
Ta có: dfrac{x^3}{y+z}+dfrac{y+z}{36}+dfrac{1}{162}+dfrac{y^3}{x+z}+dfrac{x+z}{36}+dfrac{1}{162}+dfrac{z^3}{x+y}+dfrac{x+y}{36}+dfrac{1}{162}ge3sqrt[3]{dfrac{x^3}{y+z}.dfrac{y+z}{36}.dfrac{1}{162}}+3sqrt[3]{dfrac{y^3}{x+z}.dfrac{x+z}{36}.dfrac{1}{162}}+3sqrt[3]{dfrac{z^3}{x+y}.dfrac{x+y}{36}.dfrac{1}{162}}3sqrt[3]{dfrac{x^3}{36.162}}+3sqrt[3]{dfrac{y^3}{36.162}}+3sqrt[3]{dfrac{z^3}{...
Đọc tiếp
Đề bài: ax,y,z >0 và \(\sqrt{x}+\sqrt{y}+\sqrt{z}=1\). Tìm Min P= \(\dfrac{x^3}{y+z}+\dfrac{y^3}{z+x}+\dfrac{z^3}{x+y}\).
ĐÁP ÁN:
Ta có: \(\dfrac{x^3}{y+z}+\dfrac{y+z}{36}+\dfrac{1}{162}+\dfrac{y^3}{x+z}+\dfrac{x+z}{36}+\dfrac{1}{162}+\dfrac{z^3}{x+y}+\dfrac{x+y}{36}+\dfrac{1}{162}\ge3\sqrt[3]{\dfrac{x^3}{y+z}.\dfrac{y+z}{36}.\dfrac{1}{162}}+3\sqrt[3]{\dfrac{y^3}{x+z}.\dfrac{x+z}{36}.\dfrac{1}{162}}+3\sqrt[3]{\dfrac{z^3}{x+y}.\dfrac{x+y}{36}.\dfrac{1}{162}}=3\sqrt[3]{\dfrac{x^3}{36.162}}+3\sqrt[3]{\dfrac{y^3}{36.162}}+3\sqrt[3]{\dfrac{z^3}{36.162}}=\dfrac{x+y+z}{6}.\)
=> P+\(\dfrac{x+y+z}{18}+\dfrac{1}{54}\)≥\(\dfrac{x+y+z}{6}\) <=> P≥\(\dfrac{x+y+z}{6}-\dfrac{x+y+z}{18}-\dfrac{1}{54}\)=\(\dfrac{x+y+z}{9}-\dfrac{1}{54}\)
Ta c/m đc: 3(x+y+z)≥(\(\sqrt{x}+\sqrt{y}+\sqrt{z}\))2 <=> 2(x+y+z) ≥2\(\left(\sqrt{xy}+\sqrt{xz}+\sqrt{yz}\right)\)<=> x+y+z≥\(\sqrt{xy}+\sqrt{xz}+\sqrt{yz}\)(luôn đúng)
➩x+y+z ≥ \(\dfrac{\left(\sqrt{x}+\sqrt{y}+\sqrt{z}\right)^3}{3}=\dfrac{1}{3}\) => P≥\(\dfrac{1}{54}\). Dấu ''='' xảy ra <=> x=y=z=\(\dfrac{1}{9}\)
tính
A) \(\sqrt{121}-\sqrt{\dfrac{1}{4}}+\sqrt{\dfrac{25}{36}}\)
b) \(\dfrac{3}{4}.\dfrac{-5}{7}-\dfrac{3}{4}.\dfrac{2}{7}\)
B1
a,dfrac{7}{3}.dfrac{37}{5}-dfrac{7}{3}.dfrac{32}{5}
b, 3:+left(-dfrac{3}{2}right)^2+ dfrac{1}{9}.sqrt{36}
c,left(-2right)^2 + sqrt{36}-sqrt{9}+sqrt{25}
d, left(-dfrac{2}{3}+dfrac{3}{7}right) : left(-dfrac{1}{3}+-dfrac{4}{7}right):dfrac{4}{5}
B2
a, dfrac{3}{4}+dfrac{1}{4}:x dfrac{1}{2}
b, -8 + 2 . |2x-3| 4
c, |x - dfrac{1}{3}|- sqrt{dfrac{1}{6}}sqrt{dfrac{1}{9}}
Đọc tiếp
B1
a,\(\dfrac{7}{3}\).\(\dfrac{37}{5}\)-\(\dfrac{7}{3}\).\(\dfrac{32}{5}\)
b, 3:+\(\left(-\dfrac{3}{2}\right)^2\)+ \(\dfrac{1}{9}\).\(\sqrt{36}\)
c,\(\left(-2\right)^2\) + \(\sqrt{36}\)-\(\sqrt{9}\)+\(\sqrt{25}\)
d, \(\left(-\dfrac{2}{3}+\dfrac{3}{7}\right)\) : \(\left(-\dfrac{1}{3}+-\dfrac{4}{7}\right):\dfrac{4}{5}\)
B2
a, \(\dfrac{3}{4}\)+\(\dfrac{1}{4}\):x = \(\dfrac{1}{2}\)
b, -8 + 2 . |2x-3| =4
c, |x - \(\dfrac{1}{3}\)|- \(\sqrt{\dfrac{1}{6}}\)=\(\sqrt{\dfrac{1}{9}}\)
B1
a. = 7/3. ( 37/5 - 32/5)
= 7/3 . 1
= 7/3
![]() Phần b có gì đó sai sao lại có 3:+
Phần b có gì đó sai sao lại có 3:+
c. = 4 + 6 - 3 + 5
= 12
d. = -5/21 : -19/21 : 4/5
= 25/76
B2
a. 1/4 : x =1/2 - 3/4
x = -1/4
x = 1/4 : -1/4
x = -1
b. 2 . | 2x - 3 | = 4 - (-8)
2 . | 2x - 3| = 12
| 2x - 3 | = 12:2
| 2x - 3 | = 6
| x - 3 | = 6:2
| x - 3 | = 3
=> x - 3 = +- 3
* x - 3 = 3
x = 6
* x - 3 = -3
x = 0
Chúc bạn vui vẻ ![]()
Đúng 0
Bình luận (1)
b. = 3 : 9/4 + 1/9 .6
= 4/3 + 2/3
= 2
Đúng 0
Bình luận (4)
sr mik nhầm phải là
3:\(\left(-\dfrac{3}{2}\right)^2\)+\(\dfrac{1}{9}\).\(\sqrt{36}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời