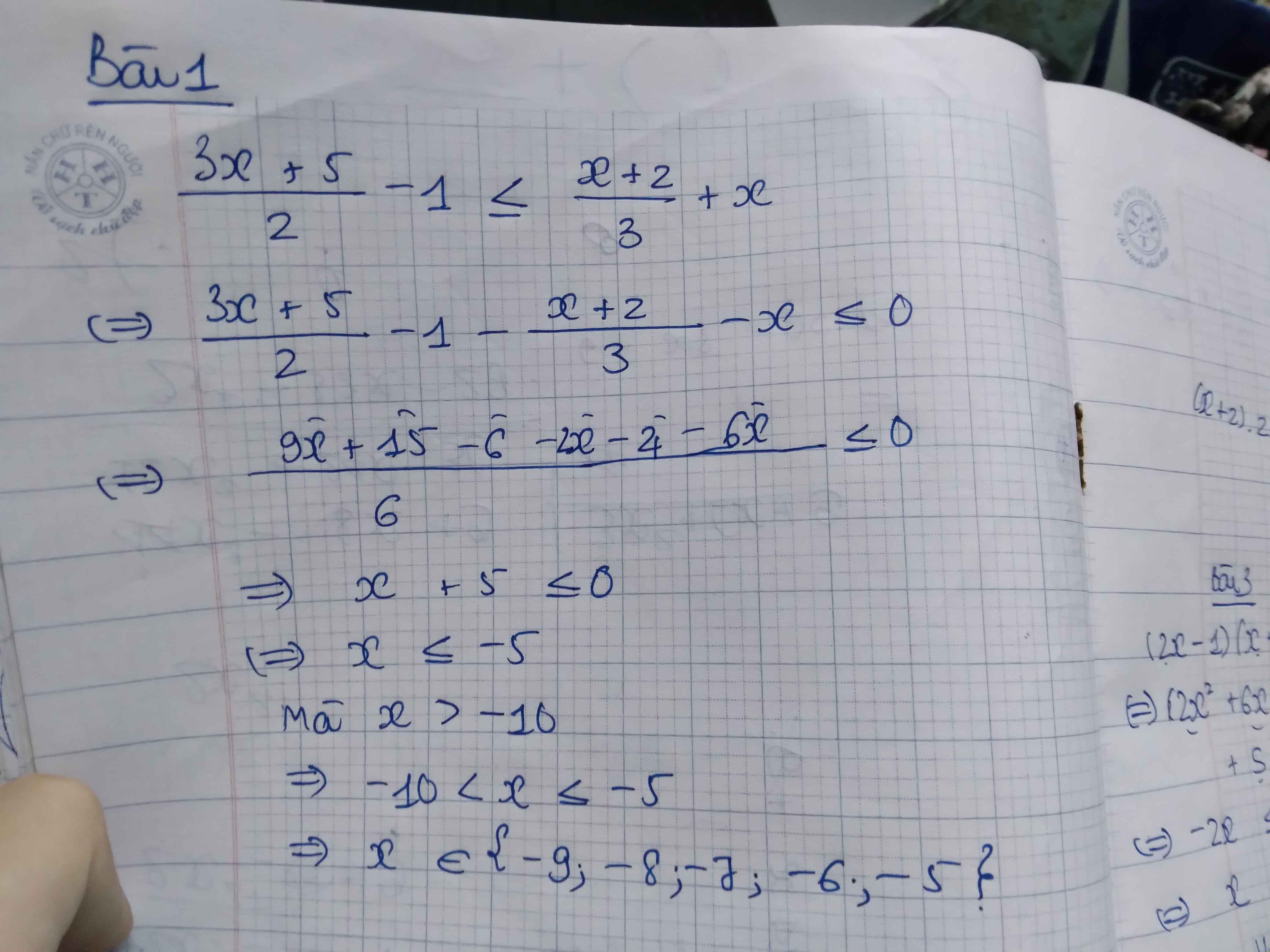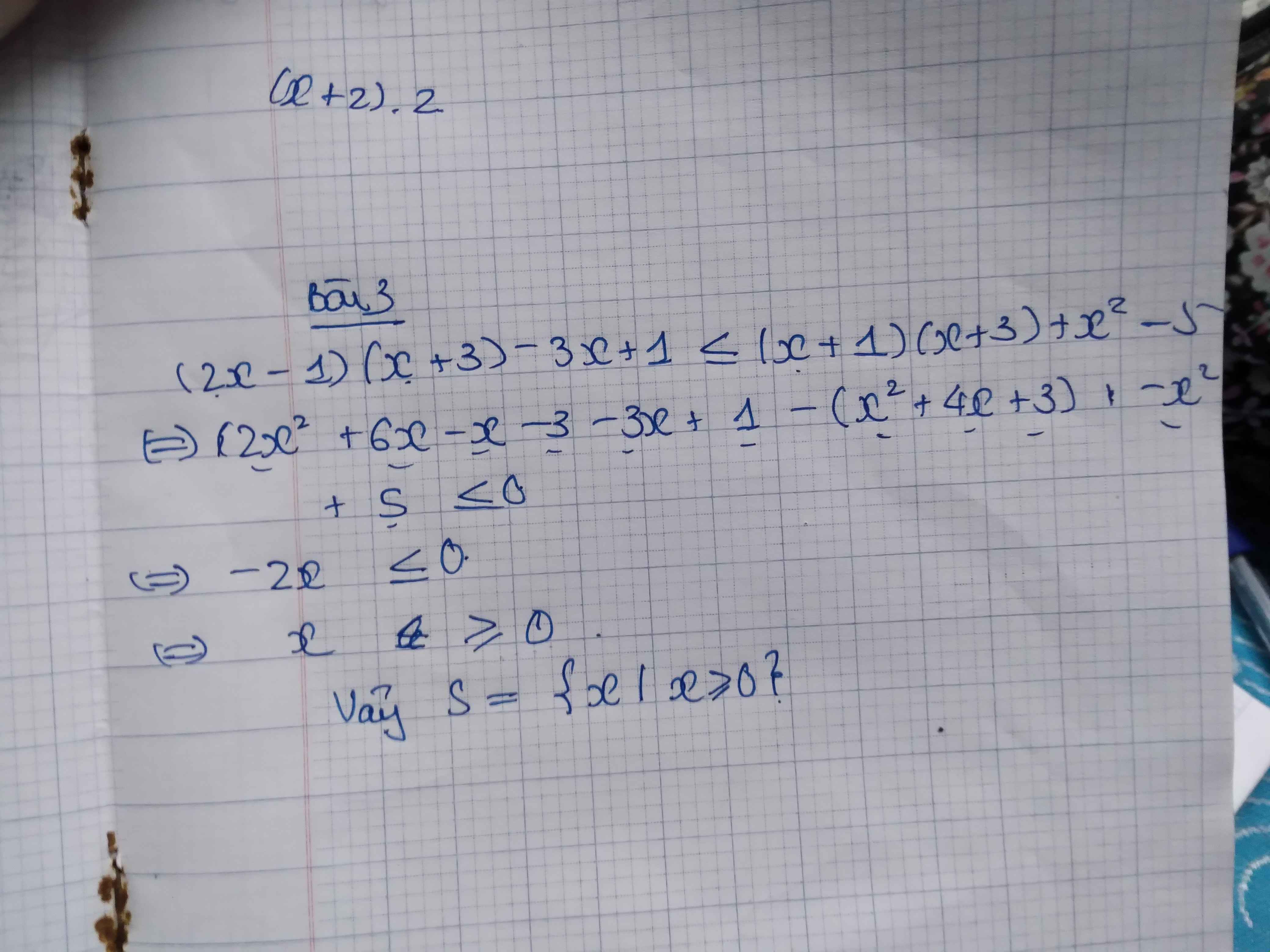tìm tập nghiệm của pt :2x +\(\dfrac{3}{x-1}\)=\(\dfrac{3x}{x-1}\)
DN
Những câu hỏi liên quan
a)Có bao nhiêu giá trị nguyên dương x thỏa mãn \(\dfrac{x+3}{x^2-4}-\dfrac{1}{x+2}< \dfrac{2x}{2x-x^2}\)
b) Tập nghiệm S của bất pt \(\dfrac{-2x^2+7x+7}{x^2-3x-10}\le-1\)
1. Tìm \(m\in\left[-10;10\right]\) để pt \(\left(x^2-2x+m\right)^2-2x^2+3x-m=0\) có 4 ng pb
2. Cho biết x1,x2 là nghiệm của pt \(x^2-x+a=0\) và x3,x4 là nghiệm của pt \(x^2-4x+b=0\) . Biết rằng \(\dfrac{x2}{x1}=\dfrac{x3}{x2}=\dfrac{x4}{x3}\), b >0 . Tìm a
1.
Đặt \(x^2-2x+m=t\), phương trình trở thành \(t^2-2t+m=x\)
Ta có hệ \(\left\{{}\begin{matrix}x^2-2x+m=t\\t^2-2t+m=x\end{matrix}\right.\)
\(\Rightarrow\left(x-t\right)\left(x+t-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=t\\x=1-t\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=x^2-2x+m\\x=1-x^2+2x-m\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-x^2+3x\\m=-x^2+x+1\end{matrix}\right.\)
Phương trình hoành độ giao điểm của \(y=-x^2+x+1\) và \(y=-x^2+3x\):
\(-x^2+x+1=-x^2+3x\)
\(\Leftrightarrow x=\dfrac{1}{2}\Rightarrow y=\dfrac{5}{4}\)
Đồ thị hàm số \(y=-x^2+3x\) và \(y=-x^2+x+1\):
Dựa vào đồ thị, yêu cầu bài toán thỏa mãn khi \(m< \dfrac{5}{4}\)
Mà \(m\in\left[-10;10\right]\Rightarrow m\in[-10;\dfrac{5}{4})\)
Đúng 3
Bình luận (1)
Tìm tập nghiệm của phương trình
a/ \(x-\sqrt{2x+3}=-2x\)
b/ \(\dfrac{1}{x}=1-\dfrac{1}{x+1}\)
c/ \(\dfrac{2}{\sqrt{x+3}}=\dfrac{1}{\sqrt{x^2-9}}\)
a) \(x-\sqrt{2x+3}=-2x\)
\(\Leftrightarrow\sqrt{2x+3}=x+2x\)
\(\Leftrightarrow\sqrt{2x+3}=3x\)
\(\Leftrightarrow2x+3=9x^2\)
\(\Leftrightarrow9x^2-2x-3=0\)
\(\Rightarrow\Delta=\left(-2\right)^2-4\cdot9\cdot\left(-3\right)=112>0\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1=\dfrac{2+\sqrt{112}}{18}=\dfrac{1+2\sqrt{7}}{9}\\x_2=\dfrac{2-\sqrt{112}}{18}=\dfrac{1-2\sqrt{7}}{9}\end{matrix}\right.\)
b) \(\dfrac{1}{x}=1-\dfrac{1}{x+1}\) (ĐK: \(x\ne0,x\ne-1\))
\(\Leftrightarrow\dfrac{1}{x}+\dfrac{1}{x+1}=1\)
\(\Leftrightarrow\dfrac{x+1}{x\left(x+1\right)}+\dfrac{x}{x\left(x+1\right)}=1\)
\(\Leftrightarrow\dfrac{x+1+x}{x\left(x+1\right)}=1\)
\(\Leftrightarrow\dfrac{2x+1}{x^2+x}=1\)
\(\Leftrightarrow2x+1=x^2+1\)
\(\Leftrightarrow x^2-2x=0\)
\(\Leftrightarrow x\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x-2=0\end{matrix}\right.\)
\(\Leftrightarrow x=2\left(tm\right)\)
Đúng 2
Bình luận (0)
c) \(\dfrac{2}{\sqrt{x+3}}=\dfrac{1}{\sqrt{x^2-9}}\) (ĐK: \(x\ge3\))
\(\Leftrightarrow2\sqrt{x^2-2}=\sqrt{x+3}\)
\(\Leftrightarrow\sqrt{4\left(x^2-9\right)}=\sqrt{x+3}\)
\(\Leftrightarrow4\left(x^2-9\right)=x+3\)
\(\Leftrightarrow4x^2-36=x+3\)
\(\Leftrightarrow4x^2-x-36-3=0\)
\(\Leftrightarrow4x^2-x-39=0\)
\(\Rightarrow\Delta=\left(-1\right)^2-4\cdot4\cdot\left(-39\right)=625>0\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1=\dfrac{1+\sqrt{625}}{8}=\dfrac{13}{4}\left(tm\right)\\x_2=\dfrac{1-\sqrt{625}}{8}=-3\left(ktm\right)\end{matrix}\right.\)
Đúng 2
Bình luận (0)
22. Tìm nghiệm dương nhỏ nhất của PT: \(3\sin^2x+2\sin x\cos x-\cos^2x=0\)
23. Giải PT: \(\sqrt{3}\cos x+2\sin^2\left(\dfrac{x}{2}-\dfrac{\pi}{1}\right)=1\)
\(\sqrt{3}cosx+2sin^2\left(\dfrac{x}{2}-\pi\right)=1\)
\(\Leftrightarrow\sqrt{3}cosx+2sin^2\dfrac{x}{2}=1\)
\(\Leftrightarrow\sqrt{3}cosx-cosx=0\Leftrightarrow cosx=0\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\) ( k thuộc Z )
Vậy ...
Đúng 0
Bình luận (0)
22.
Nhận thấy \(cosx=0\) không phải nghiệm, chia 2 vế cho \(cos^2x\)
\(3tan^2x+2tanx-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=-1\\tanx=\dfrac{1}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=arctan\left(\dfrac{1}{3}\right)+k\pi\end{matrix}\right.\)
Nghiệm dương nhỏ nhất của pt là: \(x=arctan\left(\dfrac{1}{3}\right)\)
Đúng 0
Bình luận (0)
22. PT đã cho tương đương
3 - 4cos2x + 2 sinxcosx = 0
⇔ 3 - 2 - 2cos2x + sin2x = 0
⇔ 1 - 2cos2x + sin2x = 0
⇔ 1 + sin2x = 2cos2x
⇔ sin\(\dfrac{\pi}{2}\) + sin2x = 2cos2x
⇔ \(2sin\left(\dfrac{\pi}{4}+x\right).cos\left(\dfrac{\pi}{4}-x\right)\) = 2cos2x
Do \(\left(\dfrac{\pi}{4}-x\right)+\left(\dfrac{\pi}{4}+x\right)=\dfrac{\pi}{2}\)
⇒ \(sin\left(\dfrac{\pi}{4}+x\right)=cos\left(\dfrac{\pi}{4}-x\right)\)
Vậy sin2\(\left(x+\dfrac{\pi}{4}\right)\) = cos2x
Cái này là hiển nhiên ????
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
B1
\(\dfrac{3x+5}{2}-1\le\dfrac{x+2}{3}+x\)
Có bnhieu nghiệm nguyên lớn hơn -10
BÀI 2 . Tập nghiệm S của btp\(\left(1-\sqrt{2}\right)x< 3-2\sqrt{2}\)
BÀI 3 \(\left(2X-1\right)\left(x+3\right)-3x+1\le\left(x+1\right)\left(x+3\right)+x^2-5\) có tập nghiệm là?
Bài 1 :
Ta có : \(\dfrac{3x+5}{2}-1\le\dfrac{x+2}{3}+x\)
\(\Leftrightarrow\dfrac{3x+5}{2}-1-\dfrac{x+2}{3}-x\le0\)
\(\Leftrightarrow\dfrac{3\left(3x+5\right)-6-2\left(x+2\right)-6x}{6}\le0\)
\(\Leftrightarrow9x+15-6-2x-4-6x\le0\)
\(\Leftrightarrow x\le-5\)
Mà \(\left\{{}\begin{matrix}x\in Z\\x>-10\end{matrix}\right.\)
Vậy \(x\in\left\{-5;-6;-7;-8;-9\right\}\)
Đúng 2
Bình luận (0)
b3\(\Leftrightarrow2x^2+5x-3-3x+1\le x^2+2x-3+x^2-5\\ \Leftrightarrow0.x\le-6\Leftrightarrow x\in\varnothing\)
Đúng 0
Bình luận (0)
Tìm tập xác định của hàm số :a. ydfrac{1}{x^2-2x}+sqrt{x^2-1}b.ysqrt{x+1}+sqrt{5-3x}c.ysqrt{5x+3}+dfrac{2x}{sqrt{3-x}}d.ydfrac{3x}{sqrt{4-x^2}}+sqrt{1+x}e.ydfrac{5-2x}{(2-3x)sqrt{1-6x}}
Đọc tiếp
Tìm tập xác định của hàm số :
a. y=\(\dfrac{1}{x^2-2x}+\sqrt{x^2-1}\)
b.y=\(\sqrt{x+1}+\sqrt{5-3x}\)
c.y=\(\sqrt{5x+3}+\dfrac{2x}{\sqrt{3-x}}\)
d.y=\(\dfrac{3x}{\sqrt{4-x^2}}+\sqrt{1+x}\)
e.y=\(\dfrac{5-2x}{(2-3x)\sqrt{1-6x}}\)
a: ĐKXĐ: x^2-2x<>0 và x^2-1>0
=>(x>1 và x<>2) hoặc x<-1
b: ĐKXĐ: x+1>0 và 5-3x>0
=>x>-1 và 3x<5
=>-1<x<5/3
c: DKXĐ: 5x+3>=0 và 3-x>0
=>x>=-3/5 và x<3
=>-3/5<=x<3
d: ĐKXĐ: 4-x^2>0 và 1+x>=0
=>x^2<4 và x>=-1
=>-2<x<2 và x>=-1
=>-1<=x<2
e: ĐKXĐ: 2-3x<>0 và 1-6x>0
=>x<>2/3 và x<1/6
=>x<1/6
Đúng 0
Bình luận (0)
Tập nghiệm của bất pt \(\log_{\dfrac{1}{2}}\left(x+1\right)-log_{\dfrac{1}{2}}\left(2x-1\right)< 2\)
ĐKXĐ: \(x>\dfrac{1}{2}\)
\(log_{\dfrac{1}{2}}\left(\dfrac{x+1}{2x-1}\right)< 2\)
\(\Rightarrow\dfrac{x+1}{2x-1}>\dfrac{1}{4}\)
\(\Rightarrow x>-\dfrac{5}{2}\)
Kết hợp ĐKXĐ: \(\Rightarrow x>\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
Bài 3. Giải bất phương trình và biểu diễn tập hợp nghiệm trên trục số:a) dfrac{2x + 2}{5} + dfrac{3}{10} dfrac{3x - 2}{4}b) dfrac{2 + x}{3} dfrac{3 + 2x}{5}d) 1 + dfrac{3(x + 1)}{10} dfrac{x - 2}{5}e) dfrac{2x - 7}{6} ≥ dfrac{3x - 7}{2}f) dfrac{2x - 1}{3} dfrac{3x + 1}{2}
Đọc tiếp
Bài 3. Giải bất phương trình và biểu diễn tập hợp nghiệm trên trục số:
a) \(\dfrac{2x + 2}{5} + \dfrac{3}{10} < \dfrac{3x - 2}{4}\)
b) \(\dfrac{2 + x}{3} < \dfrac{3 + 2x}{5}\)
d) \(1 + \dfrac{3(x + 1)}{10} > \dfrac{x - 2}{5}\)
e) \(\dfrac{2x - 7}{6} \) ≥ \(\dfrac{3x - 7}{2}\)
f) \(\dfrac{2x - 1}{3} > \dfrac{3x + 1}{2}\)
Giải các pt sau:1)dfrac{2x+1}{x^2-4}+dfrac{2}{x+1}dfrac{3}{2-x}2)dfrac{3x+1}{1-3x}+dfrac{3+x}{3-x}23)dfrac{8x-2}{3}1+dfrac{5-2x}{4}4)dfrac{x}{x+1}-dfrac{2x+3}{x}dfrac{-3}{x+1}-dfrac{3}{x}5)dfrac{x+1}{x-1}-dfrac{x-1}{x+1}dfrac{4}{x^2-1}6)dfrac{2x+5}{2x}-dfrac{x}{x+5}0giúp mình với cám ơn
Đọc tiếp
Giải các pt sau:
1)\(\dfrac{2x+1}{x^2-4}+\dfrac{2}{x+1}=\dfrac{3}{2-x}\)
2)\(\dfrac{3x+1}{1-3x}+\dfrac{3+x}{3-x}=2\)
3)\(\dfrac{8x-2}{3}=1+\dfrac{5-2x}{4}\)
4)
\(\dfrac{x}{x+1}-\dfrac{2x+3}{x}=\dfrac{-3}{x+1}-\dfrac{3}{x}\)
5)\(\dfrac{x+1}{x-1}-\dfrac{x-1}{x+1}=\dfrac{4}{x^2-1}\)
6)\(\dfrac{2x+5}{2x}-\dfrac{x}{x+5}=0\)
giúp mình với cám ơn
1: Sửa đề: 2/x+2
\(\dfrac{2x+1}{x^2-4}+\dfrac{2}{x+2}=\dfrac{3}{2-x}\)
=>\(\dfrac{2x+1+2x-4}{x^2-4}=\dfrac{-3\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}\)
=>4x-3=-3x-6
=>7x=-3
=>x=-3/7(nhận)
2: \(\Leftrightarrow\dfrac{\left(3x+1\right)\left(3-x\right)+\left(3+x\right)\left(1-3x\right)}{\left(1-3x\right)\left(3-x\right)}=2\)
=>9x-3x^2+3-x+3-9x+x-3x^2=2(3x-1)(x-3)
=>-6x^2+6=2(3x^2-10x+3)
=>-6x^2+6=6x^2-20x+6
=>-12x^2+20x=0
=>-4x(3x-5)=0
=>x=5/3(nhận) hoặc x=0(nhận)
3: \(\Leftrightarrow x\cdot\dfrac{8}{3}-\dfrac{2}{3}=1+\dfrac{5}{4}-\dfrac{1}{2}x\)
=>x*19/6=35/12
=>x=35/38
Đúng 0
Bình luận (0)