Lập trình pascal mn giúp mình vs a mình cảm ơn
H24
Những câu hỏi liên quan
Lập trình pascal ạ
Mn giúp mình với
uses crt;
var a:array[1..200]of real;
i,n:integer;
tb:real;
begin
clrscr;
readln(n);
for i:=1 to n do readln(a[i]);
tb:=0;
for i:=1 to n do tb:=tb+a[i];
writeln(tb/n:4:2);
readln;
end.
Đúng 0
Bình luận (0)
Lập trình pascal ạ mn giúp mình với
uses crt;
var a:array[1..100]of real;
i,n,dem:integer;
begin
clrscr;
readln(n);
for i:=1 to n do readln(a[i]);
dem:=0;
for i:=1 to n do
if a[i]>=8 then inc(dem);
writeln(dem);
readln;
end.
Đúng 0
Bình luận (0)
Em hãy viết chương trình nhập vào mảng A gồm 100 phần tử. tính và đưa ra màn hình tổng các phần tử không chia chết cho 2 trong mảng. Mn ơi giúp mình làm bài này với ạ TT mình cảm ơn mọi người nhiều!! (pascal nhé mấy bạn ơi
Var a:array[1..100] of integer;
i,s:integer;
Begin
For i:=1 to 100 do
Begin
Write('Nhap phan tu thu ',i,' = ');readln(a[i]);
If a[i] mod 2 <> 0 then s:=s+a[i];
End;
Write('Tong la ',s);
Readln;
End.
Đúng 1
Bình luận (1)
Cho hai phân số 1/a và 1/a+1 vs a là số nguyên được hay chứng minh rằng 2ps bằng hiệu của chúng
Mn giúp mình vs mình cần gấp huhu làm ơn ơn mà giúp mình vs ạ ! Mình cảm ơn nhiêù
Mn ơi giúp mình câu 4 phần 3 vs giải thích giúp mình cách làm của nó như thế nào vs mình cảm ơn mn nhiều.
3: góc AMN=góic ACM
=>AM là tiếp tuyến của đường tròn ngoại tiếp ΔECM
=>góc AMB=90 độ
=>Tâm o1 của đường tròn ngoại tiếp ΔECM nằm trên BM
NO1 min khi NO1=d(N;BM)
=>NO1 vuông góc BM
Gọi O1 là chân đường vuông góc kẻ từ N xuống BM
=>O1 là tâm đường tròn ngoại tiếp ΔECM có bán kính là O1M
=>d(N;tâm đường tròn ngoại tiếp ΔECM) nhỏ nhất khi C là giao của (O1;O1M) với (O) với O1 ;là hình chiếu vuông góc của N trên BM
Đúng 0
Bình luận (0)
Mn giúp mình vs ạ, mình cảm ơn nha

a) nAl= 0,2(mol)
PTHH: 4Al + 3 O2 -to-> 2 Al2O3
nO2= 3/4 . 0,2= 0,15(mol)
=>V(O2,đktc)=0,15.22,4=3,36(l)
Vkk(đktc)=5.V(O2,đktc)=3,36.5=16,8(l)
b) nAl=0,2(mol)
nO2=0,4(mol)
Ta có: 0,2/4 < 0,4/3
=> Al hết, O2 dư, tính theo nAl.
- Sau phản ứng có O2(dư) và Al2O3
nAl2O3= nAl/2= 0,2/2=0,1(mol)
nO2(dư)= 0,4- 0,2. 3/4=0,25(mol)
Đúng 0
Bình luận (0)
Giúp mình vs , mình cảm ơn mn trước ak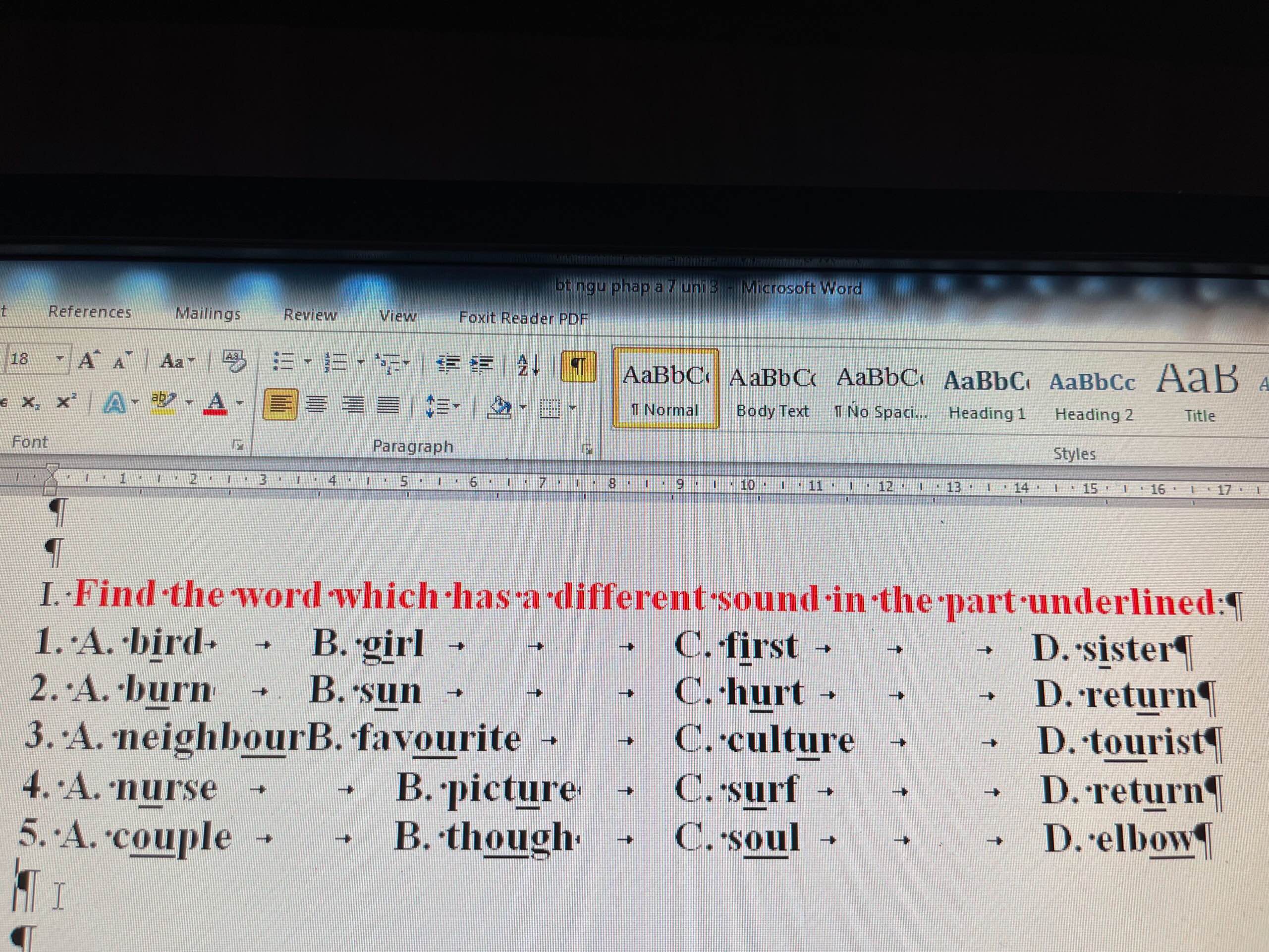
 ai giúp mình vs mình đang cần gấp
ai giúp mình vs mình đang cần gấp
cảm ơn mn vì đã giúp mình
Mn giải giúp mình vs ạ. Mình cảm ơn nhiều
- Xét : \(x^2+8x-20\le0\)
\(\Rightarrow-10\le x\le2\)
Mà \(x>0\)
\(\Rightarrow0< x\le2\)
- Xét \(x^2-2\left(m+3\right)x+m^2-2m< 0\)
Có : \(\Delta^,=b^{,2}-ac=\left(m+3\right)^2-\left(m^2-2m\right)\)
\(=m^2+6m+9-m^2+2m=8m+9\)
- Để bất phương trình có nghiệm
\(\Leftrightarrow\Delta>0\)
\(\Leftrightarrow m>-\dfrac{9}{8}\)
=> Bất phương trình có nghiệm \(S=\left(x_1;x_2\right)\)
Mà \(0< x\le2\)
\(\Rightarrow0< x_1< x_2\le2\)
\(TH1:x=2\)
\(\Rightarrow4-4\left(m+3\right)+m^2-2m< 0\)
\(\Rightarrow3-\sqrt{17}< m< 3+\sqrt{17}\)
\(TH2:0< x_1< x_2< 2\)
\(\Rightarrow\left\{{}\begin{matrix}m^2-2m>0\\m^2-6m-8>0\\0< 2\left(m+3\right)< 2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< 0\\m>2\end{matrix}\right.\\\left[{}\begin{matrix}m>3+\sqrt{17}\\m< 3-\sqrt{17}\end{matrix}\right.\\-3< m< -2\end{matrix}\right.\)
Vậy \(3-\sqrt{7}< m< 3+\sqrt{7}\)
Đúng 1
Bình luận (4)
Từ pt đầu \(\Rightarrow-10\le x\le2\) (1)
Để BPT chứa m có nghiệm thì \(\Delta'>0\Rightarrow m...\) (2)
Gọi 2 nghiệm của pt chứa m là \(x_1;x_2\Rightarrow\) miền nghiệm của BPT dưới là \(D=\left(x_1;x_2\right)\)
Do (1) chỉ chứa 2 số nguyên dương là 1 và 2, nên để hệ có nghiệm nguyên dương thì D cần chứa ít nhất 1 trong 2 giá trị 1 hoặc 2
\(\Leftrightarrow\left[{}\begin{matrix}x_1< 1< x_2\\x_1< 2< x_2\end{matrix}\right.\) (các trường hợp trùng lặp 2 điều kiện ví dụ \(x_1< 1< 2< x_2\) không thành vấn đề vì cuối cùng ta cũng hợp nghiệm)
\(\Leftrightarrow\left[{}\begin{matrix}f\left(1\right)< 0\\f\left(2\right)< 0\end{matrix}\right.\) (3) với \(f\left(x\right)=x^2-2\left(m+3\right)x+m^2-2m\)
Lấy giao nghiệm của (2) và (3) sẽ được khoảng m cần tìm
Đúng 0
Bình luận (0)




