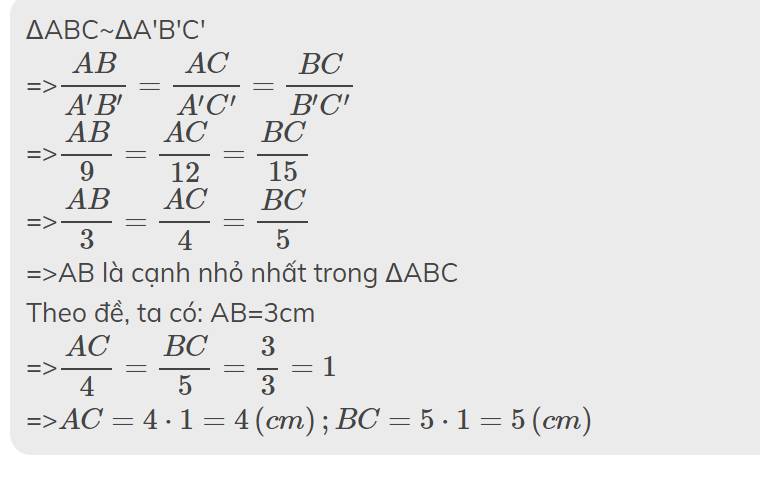Nửa chu vi của tam giác ABC là:  p = 9 + 10 + 11 2 = 15

Áp dụng công thức Hê- rông, diện tích tam giác ABC là:

S = 15 15 − 9 15 − 10 15 − 11 = 15.6.5.4 = 30 2

Chọn D.

Ta có:  cosC =   a 2 + ​ b 2 − c 2 2 a b = 8 2 + ​ 9 2 − 10 2 2.8.9 > 0

⇒ 0 0 < ​ C ^ < 90 0

Tam giác ABC có AB = c là cạnh lớn nhất. Do đó, góc C là góc lớn nhất.

Lại có:  0 0 < ​ C ^ < 90 0 nên tam giác ABC là tam giác nhọn.

Chọn A

ΔABC~ΔA'B'C'

=>\(\dfrac{AB}{A'B'}=\dfrac{AC}{A'C'}=\dfrac{BC}{B'C'}\)

=>\(\dfrac{AB}{9}=\dfrac{AC}{12}=\dfrac{BC}{15}\)

=>\(\dfrac{AB}{3}=\dfrac{AC}{4}=\dfrac{BC}{5}\)

=>AB là cạnh nhỏ nhất trong ΔABC

Theo đề, ta có: AB=3cm

=>\(\dfrac{AC}{4}=\dfrac{BC}{5}=\dfrac{3}{3}=1\)

=>\(AC=4\cdot1=4\left(cm\right);BC=5\cdot1=5\left(cm\right)\)

Câu 1:

Chú ý độ dài 3 cạnh của tam giác là sai thì \(a+b=7=c\) 

Nếu là cạnh của tam giác thì: \(\left\{{}\begin{matrix}a+b>c\\a+c>b\\c+b>a\end{matrix}\right.\) 

Câu 2: Ta có: 

\(m_a=\sqrt{\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}}=\sqrt{\dfrac{AC^2+AB^2}{2}-\dfrac{BC^2}{4}}\)

\(\Rightarrow m_a=\sqrt{\dfrac{9^2+4^2}{2}-\dfrac{6^2}{4}}\)

\(\Rightarrow m_a\approx6,3\) 

Ta có: \(p=\dfrac{AB+AC+BC}{2}=\dfrac{4+6+9}{2}=\dfrac{19}{2}\)

\(\Rightarrow S_{ABC}=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}=\sqrt{\dfrac{19}{2}\cdot\left(\dfrac{19}{2}-6\right)\cdot\left(\dfrac{19}{2}-9\right)\cdot\left(\dfrac{19}{2}-4\right)}\approx9,5\) 

\(\Rightarrow h_b=2\cdot\dfrac{S_{ABC}}{b}\Rightarrow h_b=2\cdot\dfrac{9,5}{9}\approx2,1\) 

ửa chu vi tam giác:  p = 7 + 8 + 9 2 = 12

Áp dụng công thức Hê- rông, diện tích tam giác ABC

S = 12 12 − 7 12 − 8 12 − 9 = 12.5.4.3 = 12 5

Bán kính đường tròn nội tiếp của tam giác là r = S p = 12 5 12 = 5  

ĐÁP ÁN C

1: \(\cos70^0=\dfrac{AB^2+BC^2-AC^2}{2\cdot AB\cdot BC}\)

\(\Leftrightarrow48,68-AC^2=13,57\)

hay \(AC=5,93\left(cm\right)\)

Bc 5, ac 8

Vì ∆ A’B’C’ đồng dạng với tam giác ABC nên A′B′AB=A′C′AC=B′C′BCA′B′AB=A′C′AC=B′C′BC  (1)

Thay AB = 3(cm), AC = 7 (cm), BC = 5 (cm) , A’B’ = 4,5 (cm) vào (1)

ta có: 4,5/3=A′C′/7=B′C′/5 (cm)

Vậy: A’C’ =7.4,5/3=10,5=7.4,53=10,5 (cm)

B’C’ =5.4,5/3=7,5 (cm).

*Bạn tự vẽ hình nha*

a) Xét Δ ABC vuông tại A, có:

   Góc B + góc C = 90°

⇒ Góc C= 90° - Góc B= 90° - 50°= 40°

Theo tỉ số lượng giác của góc nhọn ta có:

· AC =BC.SinB = 50. Sin50°= 38,3 (cm)

· AB = BC. SinC= 50. Sin40°= 32,1 (cm)

Sai chỗ nào thì bảo mình nhen !

Bạn ơi, Tích ✅ cho mình với