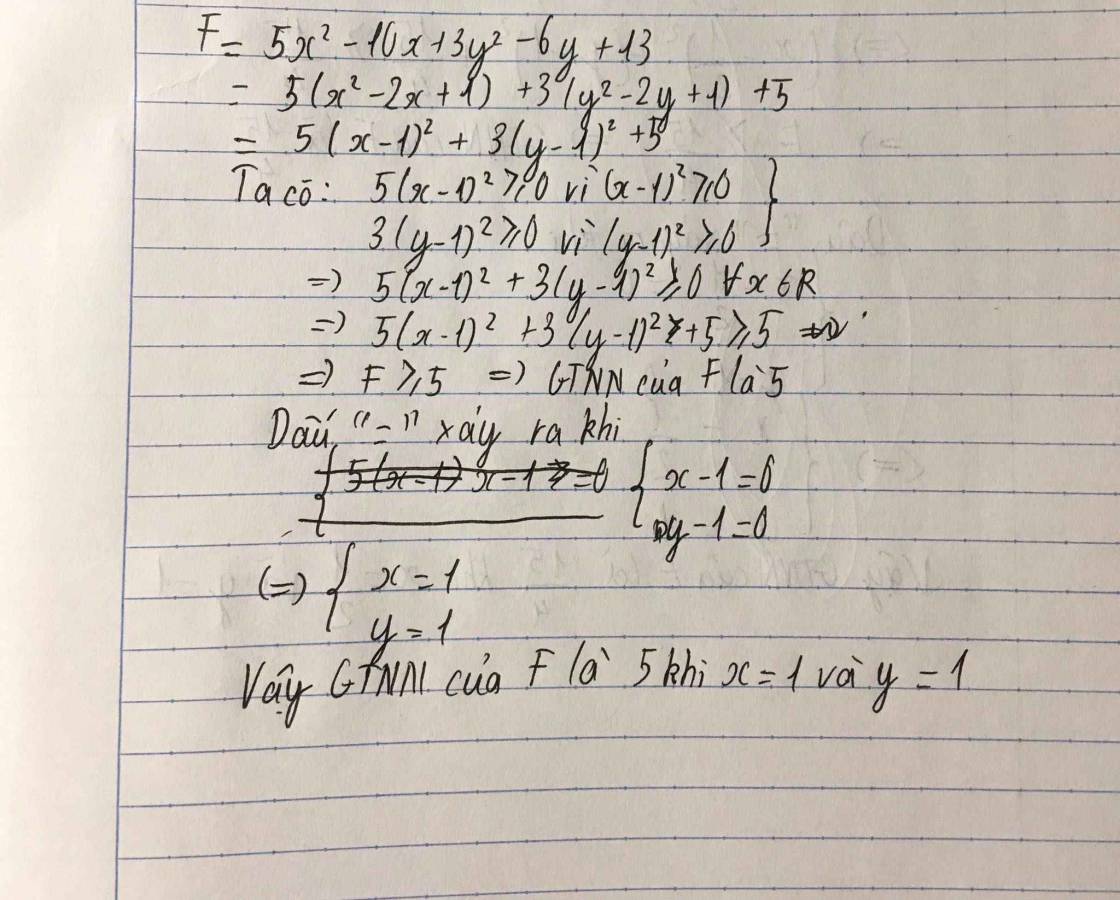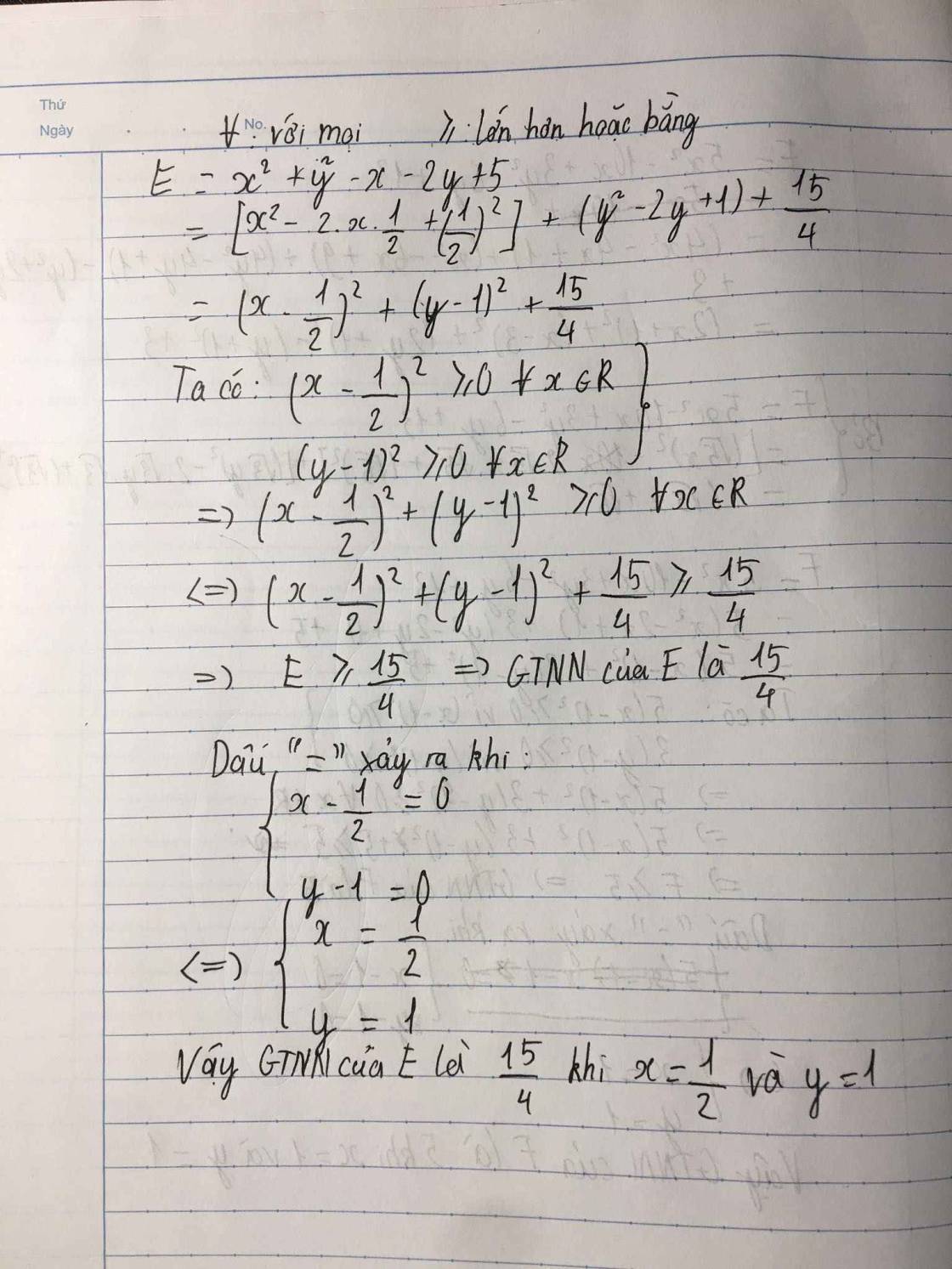Tìm x: 5x2 + 8x - 13 = 0
DN
Những câu hỏi liên quan
B1: Tìm x, a) 2x2-5x2+6x+13=0 b)x2-5x=-4
a) \(2x^2-5x^2+6x+13=0\)
\(\Leftrightarrow-3x^2+6x+13=0\)
\(\Leftrightarrow3x^2-6x-13=0\left(1\right)\)
\(\Delta'=9+39=48>0\Rightarrow\sqrt[]{\Delta'}=4\sqrt[]{3}\)
Pt (1) có 2 nghiệm phân biệt là :
\(\left[{}\begin{matrix}x=\dfrac{3+4\sqrt[]{3}}{3}=1+\dfrac{4\sqrt[]{3}}{3}\\x=\dfrac{3-4\sqrt[]{3}}{3}=1-\dfrac{4\sqrt[]{3}}{3}\end{matrix}\right.\)
b) \(x^2-5x=-4\)
\(\Leftrightarrow x^2-5x+4=0\)
\(\Leftrightarrow x^2-x-4x+4=0\)
\(\Leftrightarrow x\left(x-1\right)-4\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=4\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tìm đa thức K biết: ( 5x2 - 7x2y3 + 3y4 ) - K = 3x2 - 7x2y3 - 3y4
3x^2-8x+5-k=-2k+4x-6+x^2
\(\left(5x^2-7x^2y^3+3y^4\right)-K=3x^2-7x^2y^3-3y^4\)
\(\Rightarrow K=\left(5x^2-7x^2y^3+3y^4\right)-\left(3x^2-7x^2y^3-3y^4\right)\)
\(\Rightarrow K=5x^2-7x^2y^3+3y^4-3x^2+7x^2y^3+3y^4\)
\(\Rightarrow K=2x^2+6y^4\)
________________
\(3x^2-8x+5-K=-2K+4x-6+x^2\)
\(\Rightarrow-K+2K=\left(4x-6+x^2\right)-\left(3x^2-8x+5\right)\)
\(\Rightarrow K=4x-6+x^2-3x^2+8x-5\)
\(\Rightarrow K=-2x^2+12x-11\)
Đúng 2
Bình luận (1)
Giải các bất phương trình sau:a)
2
x
−
7
11
−
4
x
;
b)
x
−
2
2
−
x
2
−
8
x
+
3
≥
0
;
c)
2
3
−
3...
Đọc tiếp
Giải các bất phương trình sau:
a) 2 x − 7 > 11 − 4 x ; b) x − 2 2 − x 2 − 8 x + 3 ≥ 0 ;
c) 2 3 − 3 x − 6 2 > 1 + 3 x 6 ; d) x − 5 x + 1 + 4 x + 3 < − 5 x 2
Tìm x biết -4(2x+9)-(-8x+3)-(x+13)=0
Ta co´:
-4 ( 2x + 9 ) - ( -8x + 3 ) - ( x + 13 ) = 0
-8x - 36 + 8x -3 - x - 13 = 0
. ( -8x + 8x ) - 36 - 3 - x - 13 = 0
- 36 - 3 - x - 13 = 0
x = 0 + 36 + 3 + 13
x = 52
Đúng 0
Bình luận (0)
tìm cặp số nguyên x, y thỏa mãn x^2 -2xy+3y^2 +8x-8y+13=0
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+8\left(x-y\right)+16=3-2y^2\)
\(\Leftrightarrow\left(x-y\right)^2+8\left(x-y\right)+16=3-2y^2\)
\(\Leftrightarrow\left(x-y+4\right)^2=3-2y^2\) (1)
Do \(\left(x-y+4\right)^2\ge0;\forall x,y\)
\(\Rightarrow3-2y^2\ge0\Rightarrow y^2\le\dfrac{3}{2}\Rightarrow\left[{}\begin{matrix}y^2=0\\y^2=1\end{matrix}\right.\)
\(\Rightarrow y=\left\{-1;0;1\right\}\)
- Với \(y=-1\) thay vào (1):
\(\left(x+5\right)^2=1\Rightarrow\left[{}\begin{matrix}x+5=1\\x+5=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=-4\\x=-6\end{matrix}\right.\)
- Với \(y=1\) thay vào (1):
\(\Rightarrow\left(x+3\right)^2=1\Rightarrow\left[{}\begin{matrix}x+3=1\\x+3=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=-2\\x=-4\end{matrix}\right.\)
- Với \(y=0\)
\(\Rightarrow\left(x+4\right)^2=3\) (ko có nghiệm nguyên do 3 ko phải SCP)
Đúng 4
Bình luận (0)
tìm GTLN của biểu thức
D=2023-8x+2y+4xy-y2-5x2
\(D=2023-8x+2y+4xy-y^2-5x^2\)
\(=-\left(y^2+5x^2-4xy-2y+8x-2023\right)\)
\(=-\left(y^2-2.y.\left(2x+1\right)+\left(2x+1\right)^2-\left(2x+1\right)^2+5x^2+8x-2023\right)\)
\(=-\left[\left(y-2x-1\right)^2-4x^2-4x-1+5x^2+8x-2023\right]\)
\(=-\left[\left(y-2x-1\right)^2+x^2+4x-2024\right]\)
\(=-\left[\left(y-2x-1\right)^2+\left(x+2\right)^2\right]+2028\)
Vì \(-\left[\left(y-2x-1\right)^2+\left(x+2\right)^2\right]\le0\forall x,y\)
\(MaxD=2028\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-3\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Câu 13. (1,0 điểm) Cho đa thức f(x) ax2 + bx + c. a) Chứng tỏ rằng nếu a + b + c 0 thì đa thức f(x) có một nghiệm x 1.b) Áp dụng tìm một nghiệm của đa thức: f(x) 5x2 – 6x + 1
Đọc tiếp
Câu 13. (1,0 điểm) Cho đa thức f(x) = ax2 + bx + c.
a) Chứng tỏ rằng nếu a + b + c = 0 thì đa thức f(x) có một nghiệm x = 1.
b) Áp dụng tìm một nghiệm của đa thức: f(x) = 5x2 – 6x + 1
a: f(1)=a+b+c=0
=>x=1 là nghiệm
b: Vì 5-6+1=0
nên f(x)=5x^2-6x+1 có một nghiệm là x=1
Đúng 0
Bình luận (0)
tìm GTNN của biểu thức A=5x2+2y2-4xy-8x-4y+19
A=5x2+2y2−4xy−8x−4y+19=(2x2−4xy+2y2)+4(x−y)+(3x2−12x)+19=2(x−y)2+4(x−y)+3(x2−4x+4)+7=2[(x−y)2+2(x−y)+1]+3(x−2)2+5=2(x−y+1)2+3(x−2)2+5≥0Dấu "=" xảy ra khi{x−y+1
Đúng 0
Bình luận (0)
Khách vãng lai đã xóa
mik viết 5x2 là 5x mũ 2 nha
tìm x
5x2 - 15x = 0
5x2 - 15x = 0
5x(x-3)=0
suy ra 2 trường hợp
x=0
x-3=0=>x=3
Đúng 0
Bình luận (0)
5x2-15x=0
5x(x-3) =0
TH1: 5x=0 TH2: x-3=0
=>x=0 => x=3
Vậy x thuộc {0;3}
Đúng 1
Bình luận (0)
tìm GTNN của biểu thức
E=x2+y2-x-2y+5
F=5x2-10x+3y2-6y+13