\(\left(x-11\right)^{20}>=0\forall x\)

\(\left|y+68\right|^{23}>=0\forall y\)

Do đó: \(\left(x-11\right)^{20}+\left|y+68\right|^{23}>=0\forall x,y\)

Dấu '=' xảy ra khi x-11=0 và y+68=0

=>x=11 và y=-68

\(\sqrt{x+2\sqrt{2x-4}}+\sqrt{x-2\sqrt{2x-4}}=2\sqrt{2}\)

\(\Leftrightarrow\sqrt{x+2\sqrt{2\left(x-2\right)}}+\sqrt{x-2\sqrt{2\left(x-2\right)}}=2\sqrt{2}\)

\(\Leftrightarrow2x+2\sqrt{\left[x+2\sqrt{2\left(x-2\right)}\text{ }\right]\left[x-2\sqrt{2\left(x-2\right)}\text{ }\right]}=8\)

\(\Leftrightarrow2\sqrt{\left[x+2\sqrt{2\left(x-2\right)}\text{ }\right]\left[x-2\sqrt{2\left(x-2\right)}\text{ }\right]}=8-2x\)

\(\Leftrightarrow4\left[x+2\sqrt{2\left(x-2\right)}\text{ }\right]\left[x-2\sqrt{2\left(x-2\right)}\text{ }\right]=64-32x+4x^2\)

\(\Leftrightarrow4x^2-32x+64=64-32x+4x^2+\)

\(\Leftrightarrow64=64\) (Đúng)

⇒ Phương trình có vô số nghiệm.

Vậy \(S=\mathbb R\).

\(\sqrt{x+2\sqrt{2x-4}}+\sqrt{x-2\sqrt{2x-4}}=2\sqrt{2}\)

ĐK: \(x\ge2\), PT tương đương với:

\(x+2\sqrt{2x-4}+2\sqrt{\left(x+2\sqrt{2x-4}\right)\left(x-2\sqrt{2x-4}\right)}+x-2\sqrt{2x-4}=8\)

\(\Leftrightarrow2x+2\sqrt{x^2-4\left(2x-4\right)}=8\)

\(\Leftrightarrow2x+2\sqrt{x^2-8x+16}=8\\ \Leftrightarrow x+\left|x-4\right|=8\)

Với x < 4 => \(x+4-x=8\)

\(\Leftrightarrow4=8\) (loại)

Với \(x\ge4\) => \(x+x-4=8\)

\(\Leftrightarrow x=6\) (thỏa mãn)

\(x\left[\left(x+y\right)^2-\left(x-y\right)^2\right]\\ =x\left[\left(x+y-x+y\right)\left(x+y+x-y\right)\right]\\ =x.2y.2x\\ =4x^2y\)

\(x\left[\left(x+y\right)^2-\left(x-y\right)^2\right]\)

\(=x\left[x^2+2xy+y^2-\left(x^2-2xy+y^2\right)\right]\)

\(=x\left(x^2+2xy+y^2-x^2+2xy-y^2\right)\)

\(=x\cdot4xy\)

\(\)\(=4x^2y\)

\(x\left[\left(x+y\right)^2-\left(x-y\right)^2\right]\)

\(=x\left[x^2+2xy+y^2-x^2+2xy-y^2\right]\)

\(=x.4xy\)

\(=4x^2y\)

\(\infty x0=0\)

Đây chính là kết quả đúng

Tất cả mọi số thuộc R x 0  =  0

kkkkkkkkkkk đngs cho mk

Bằng 0

0 thôi bạn

vô tận nhân 0 bằng 0

HT

Ta có : 

Số 20 khi nhân với 1 số sẽ tạo ra 1 chữ số 0 ở tích .

Số 25 khi nhân với 1 số sẽ tạo ra 2 chữ số 0 ở tích .

Số 30 khi nhân với 1 số sẽ tạo ra 1 chữ số 0 ở tích .

Số 35 khi nhân với 1 số sẽ tạo ra 1 chữ số 0 ở tích .

Số 40 khi nhân với 1 số sẽ tạo ra 1 chữ số 0 ở tích .

Số 45 khi nhân với 1 số sẽ tạo ra 1 chữ số 0 ở tích .

Số 50 khi nhân với 1 số sẽ tạo ra 2 chữ số 0 ở tích . 

Vậy có 9 chữ số 0 ở tích .

Giải :
Trong tích đó có các thừa số chia hết cho 5 là :
5, 10, 15, 20, 25, 30, 35, 40, 45.
Hay 5 = 1 x 5 ; 10 = 2 x 5 ; 15 = 3 x 5; ........; 45 = 9 x 5.
Mỗi thừa số 5 nhân với 1 số chẵn cho ta 1 số tròn chục. mà tích trên có 10 thừa số 5 nên tích tận cùng bằng 10 chữ số 0.

Trong tích đó có các thừa số chia hết cho 5 là :
5, 10, 15, 20, 25, 30, 35, 40, 45.
Hay 5 = 1 x 5 ; 10 = 2 x 5 ; 15 = 3 x 5; ........; 45 = 9 x 5.
Mỗi thừa số 5 nhân với 1 số chẵn cho ta 1 số tròn chục. mà tích trên có 10 thừa số 5 nên tích tận cùng bằng 10 chữ số 0.

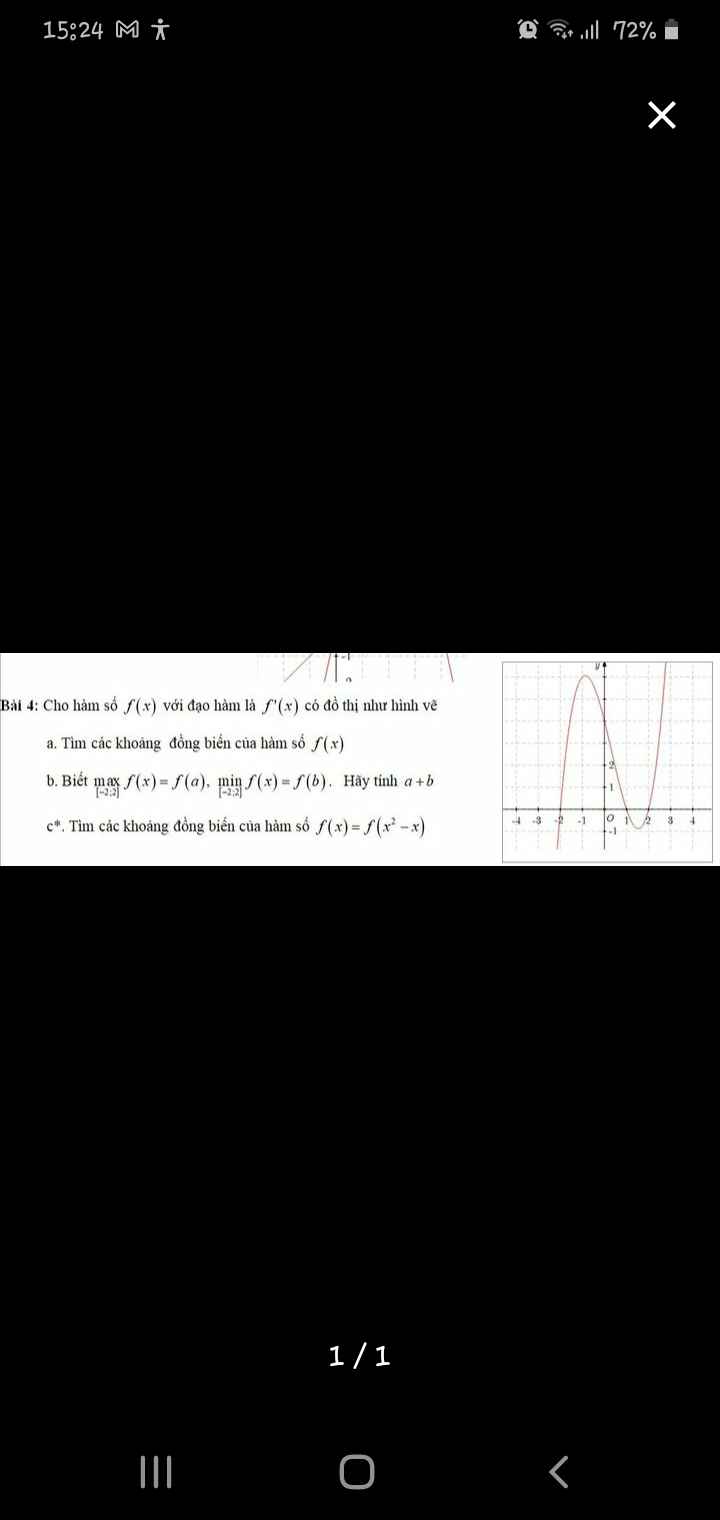
Từ đồ thị \(f'\left(x\right)\) ta có BBT hàm \(f\left(x\right)\) như sau:

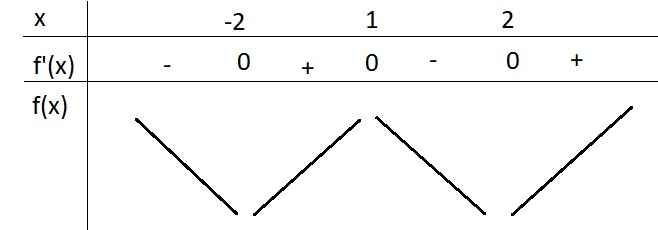
Từ đó ta thấy hàm \(f\left(x\right)\) đồng biến trên các khoảng \(\left(-2;1\right)\) và \(\left(2;+\infty\right)\)

Cũng từ BBT, trên \(\left[-2;2\right]\) ta thấy \(\max\limits_{\left[-2;2\right]}f\left(x\right)=f\left(1\right)\)

Diện tích giới hạn bởi phần đồ thị \(f'\left(x\right)\) và trục hoành trên \(\left[-2;1\right]\) lớn hơn đoạn \(\left[1;2\right]\)

\(\Rightarrow\int\limits^1_{-2}\left|f'\left(x\right)\right|dx>\int\limits^2_1\left|f'\left(x\right)\right|dx\Rightarrow\int\limits^1_{-2}f'\left(x\right)dx>\int\limits^1_2f'\left(x\right)dx\)

\(\Rightarrow f\left(1\right)-f\left(-2\right)>f\left(1\right)-f\left(2\right)\)

\(\Rightarrow f\left(2\right)>f\left(-2\right)\)

\(\Rightarrow\min\limits_{\left[-2;2\right]}f\left(x\right)=f\left(-2\right)\)

\(\Rightarrow a+b=1+\left(-2\right)=-1\)

Ta có : X ---------> 2Ag

\(n_{Ag}=0,2\left(mol\right)\Rightarrow n_X=0,1\left(mol\right)\)

Muối gồm HCOONa và RONa 

Ta có : \(n_{HCOONa}=n_{RONa}=0,1\left(mol\right)\)

=> \(0,1.68+0,1.\left(R+39\right)=18,4\)

=> R=77 (C6H5)

Vậy CTHH của este HCOOC6H5

a) Ta có: \(4\left(x-2\right)^2+xy-2y\)

\(=4\left(x-2\right)^2+y\left(x-2\right)\)

\(=\left(x-2\right)\left(4x-8+y\right)\)

b) Ta có: \(x\left(x-y\right)^3-y\left(y-x\right)^2-y^2\left(x-y\right)\)

\(=x\left(x-y\right)^3-y\left(x-y\right)^2-y^2\left(x-y\right)\)

\(=\left(x-y\right)\left[x\left(x-y\right)^2-y\left(x-y\right)-y^2\right]\)

Chỉ thấy bài 5 với 6:

5.

\(f'\left(x\right)+2f\left(x\right)=0\Leftrightarrow f'\left(x\right)=-2f\left(x\right)\Leftrightarrow\dfrac{f'\left(x\right)}{f\left(x\right)}=-2\)

Lấy nguyên hàm 2 vế:

\(\int\dfrac{f'\left(x\right)}{f\left(x\right)}dx=\int-2dx\Rightarrow ln\left(f\left(x\right)\right)=-2x+C\)

Thay \(x=1\Rightarrow0=-2+C\Rightarrow C=2\)

\(\Rightarrow ln\left(f\left(x\right)\right)=-2x+2\Rightarrow f\left(x\right)=e^{-2x+2}\)

\(\Rightarrow f\left(-1\right)=e^4\)

6.

\(f\left(x\right)+x.f'\left(x\right)=2x+1\)

\(\Leftrightarrow x'.f\left(x\right)+x.f'\left(x\right)=2x+1\)

\(\Leftrightarrow\left[x.f\left(x\right)\right]'=2x+1\)

Lấy nguyên hàm 2 vế:

\(\int\left[x.f\left(x\right)\right]'dx=\int\left(2x+1\right)dx\)

\(\Rightarrow x.f\left(x\right)=x^2+x+C\)

Thay \(x=1\Rightarrow1.f\left(1\right)=1+1+C\Rightarrow C=1\)

\(\Rightarrow f\left(x\right)=\dfrac{x^2+x+1}{x}\)

\(\Rightarrow f\left(2\right)=\dfrac{7}{2}\)

Ủa sao đề khác rồi:

3.

\(f'\left(x\right)=-e^x.f^2\left(x\right)\Leftrightarrow\dfrac{f'\left(x\right)}{f^2\left(x\right)}=-e^x\)

Lấy nguyên hàm 2 vế:

\(\int\dfrac{f'\left(x\right)}{f^2\left(x\right)}dx=\int-e^xdx\)

\(\Rightarrow\dfrac{1}{f\left(x\right)}=e^x+C\)

Thay \(x=0\Rightarrow2=1+C\Rightarrow C=1\)

\(\Rightarrow\dfrac{1}{f\left(x\right)}=e^x+1\Rightarrow f\left(x\right)=\dfrac{1}{e^x+1}\)

\(\Rightarrow f\left(ln2\right)=\dfrac{1}{3}\)