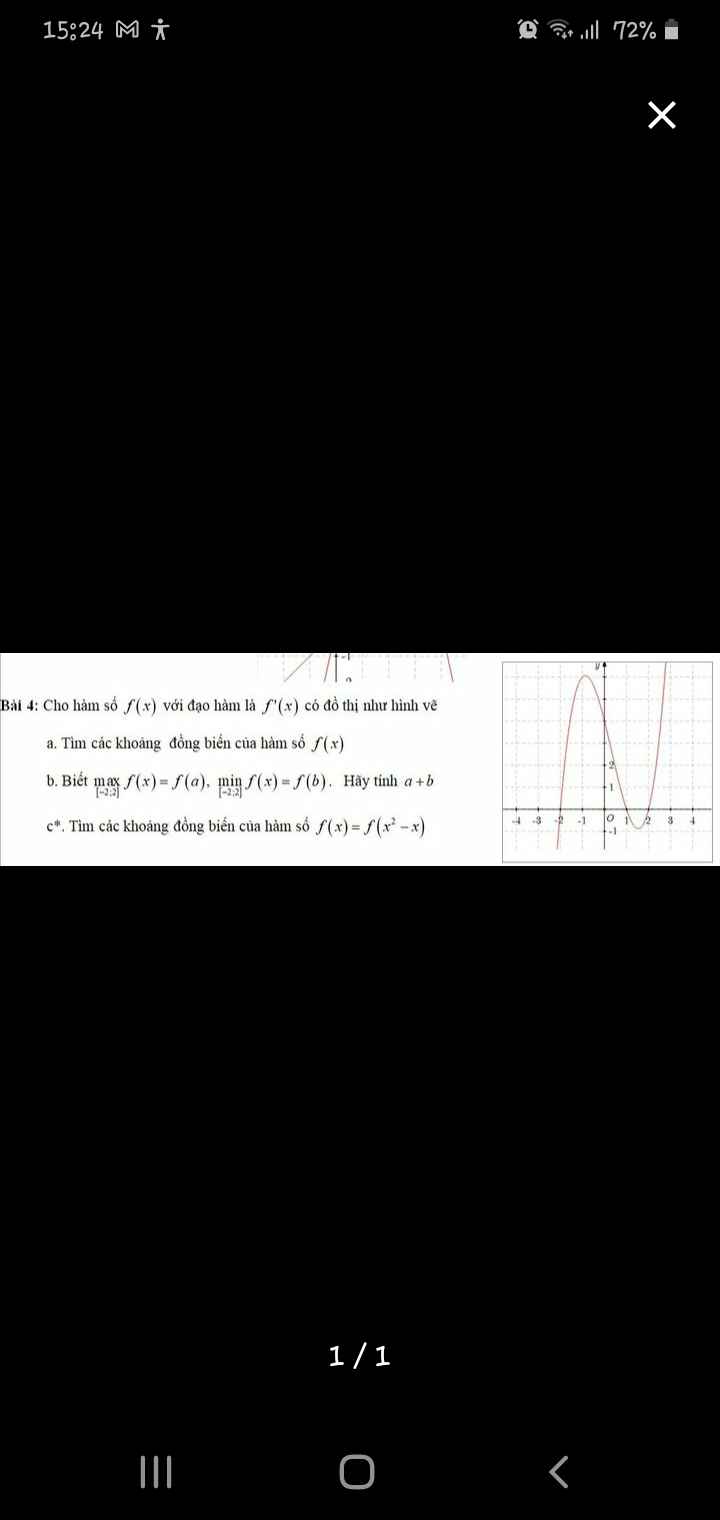
Từ đồ thị \(f'\left(x\right)\) ta có BBT hàm \(f\left(x\right)\) như sau:
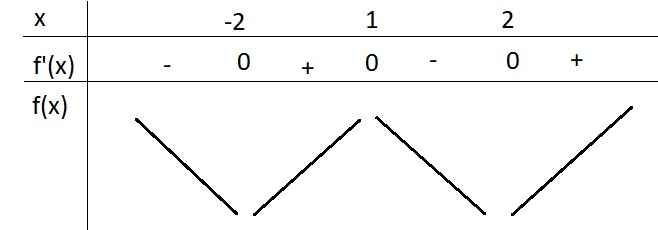
Từ đó ta thấy hàm \(f\left(x\right)\) đồng biến trên các khoảng \(\left(-2;1\right)\) và \(\left(2;+\infty\right)\)
Cũng từ BBT, trên \(\left[-2;2\right]\) ta thấy \(\max\limits_{\left[-2;2\right]}f\left(x\right)=f\left(1\right)\)
Diện tích giới hạn bởi phần đồ thị \(f'\left(x\right)\) và trục hoành trên \(\left[-2;1\right]\) lớn hơn đoạn \(\left[1;2\right]\)
\(\Rightarrow\int\limits^1_{-2}\left|f'\left(x\right)\right|dx>\int\limits^2_1\left|f'\left(x\right)\right|dx\Rightarrow\int\limits^1_{-2}f'\left(x\right)dx>\int\limits^1_2f'\left(x\right)dx\)
\(\Rightarrow f\left(1\right)-f\left(-2\right)>f\left(1\right)-f\left(2\right)\)
\(\Rightarrow f\left(2\right)>f\left(-2\right)\)
\(\Rightarrow\min\limits_{\left[-2;2\right]}f\left(x\right)=f\left(-2\right)\)
\(\Rightarrow a+b=1+\left(-2\right)=-1\)