Xác định phần dư R(x) của phép chia:
P(x)=1+x+x9+x25+x49 +x81 cho x³-x. Rồi tính R(701,4)
NY
Những câu hỏi liên quan
xác định phần dư R(x) của phép chia P(x) = 1+ x+ x9 +x25+ x49+ x81 chia cho x3- x rồi tính R(701,4)
giúp mình với .... giải từng bước để mình dễ hiểu nhé... c,ơn nhìu :)
Do \(x^3-x\) có bậc 3 => R(x) có bậc tối đa là bậc 2
\(\Rightarrow\)Đặt \(R\left(x\right)=ax^2+bx+c\) và gọi Q(x) là phần thương số, ta được:
\(x^{81}+x^{49}+x^{25}+x^9+x+1=\left(x^3-x\right)Q\left(x\right)+ax^2+bx+c\) (1)
Cho \(x=0\Rightarrow\) (1)\(\Leftrightarrow1=c\)
Cho \(x=1\) thì \(\left(1\right)\Leftrightarrow6=a+b+1\Rightarrow a+b=5\) (2)
Cho \(x=-1\) thì \(\left(1\right)\Leftrightarrow-4=a-b+1\Rightarrow a-b=-5\) (2)
Từ (2) và (3) có hệ \(\left\{{}\begin{matrix}a+b=5\\a-b=-5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=0\\b=5\end{matrix}\right.\)
Vậy phần dư là \(R\left(x\right)=5x+1\)
Đúng 0
Bình luận (2)
Xác định phần dư R(x) khi chia đa thức P(x)= 1+x^7+ X^9+x^10+X^2010+x^2011 cho Q(X)+x^3-x. Tính R(79,102011)
Xác định phần dư R(x) khi chia đa thức P(x)= 1+x^7+ X^9+x^10+X^2010+x^2011 cho Q(X)+x^3-x. Tính R(79,102011)
Quy tắc sau đây cho ta biết CAN, CHI của năm X nào đó.
Để xác định CAN, ta tìm số dư
r
trong phép chia X cho
10
và tra vào bảng 1.
r
0
1
2
3
4
5
6
7
8
9
CAN Canh Tân Nhâm Quý Giáp Ất Bính Đinh Mậu Kỷ
Để xác định CHI, ta tìm số dư
s
trong phép chia X cho
12
và tra vào bảng 2.
s
0
1
2
3
4
5
6
7
8
9
10
11
CHI Thân Dậu Tuất Hợi Tí Sửu Dần Mẹo Thìn Tỵ Ngọ Mùi
Ví dụ: năm
2020
có CAN là Canh, CHI là Tí.
a. Em hãy sữ dụng quy tắc trên để xác định CAN, CHI của năm
2023?
b. Lý Thái Tổ ( Lý Công...
Đọc tiếp
Quy tắc sau đây cho ta biết CAN, CHI của năm X nào đó. Để xác định CAN, ta tìm số dư r trong phép chia X cho 10 và tra vào bảng 1. r 0 1 2 3 4 5 6 7 8 9 CAN Canh Tân Nhâm Quý Giáp Ất Bính Đinh Mậu Kỷ Để xác định CHI, ta tìm số dư s trong phép chia X cho 12 và tra vào bảng 2. s 0 1 2 3 4 5 6 7 8 9 10 11 CHI Thân Dậu Tuất Hợi Tí Sửu Dần Mẹo Thìn Tỵ Ngọ Mùi Ví dụ: năm 2020 có CAN là Canh, CHI là Tí. a. Em hãy sữ dụng quy tắc trên để xác định CAN, CHI của năm 2023? b. Lý Thái Tổ ( Lý Công Uẩn) là vị vua đầu tiên đã mở nên triều đại Lý Phồn Thịnh trong suốt hơn 200 năm. Ông lên ngôi vào năm Kỷ Dậu đầu thế kỉ 11. Em hãy cho biết ông lên ngôi vào năm nào ?
Nó bị lỗi tý mong mn nhìn dc và giúp mình ạ
Đúng 0
Bình luận (0)
b: 1010
a: Năm nay là năm Quý Mão
Đúng 0
Bình luận (1)
Tính rồi thử lại (theo mẫu):
8192 : 32;
15335 : 42
Chú ý: phép chia hết: a : b = c, ta có a = b x c (b > 0)
Phép chia có dư: a : b = c (dư r), ta có a = b x c + r (0 < r < b).
Tính rồi thử lại (theo mẫu):
75,95 : 3,5
97,65 : 21,7
Chú ý: phép chia hết: a : b = c, ta có a = b x c (b > 0)
Phép chia có dư: a : b = c (dư r), ta có a = b x c + r (0 < r < b).
Chia đa thức \(P\left(x\right)=1+x^4+x^{16}+x^{36}+x^{64}\) cho x3 - xta được phần dư là R(x).
a ) Xác định R(x)
b ) Tính giá trị đúng của R(20172018)
Trong mỗi trường hợp sau đây, tìm thương Q(x) và dư R(x) trong phép chia F(x) cho G(x) rồi biểu diễn F(x) dưới dạng:
F(x) = G(x) . Q(x) + R(x)
a) F(x) = 6x4 – 3x3 + 15x2 + 2x – 1 ; G(x) = 3x2
b) F(x) = 12x4 + 10x3 – x – 3 ; G(x) = 3x2 + x + 1
a)
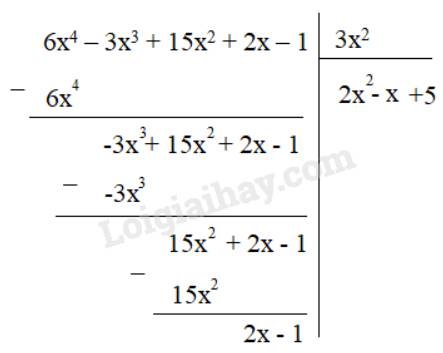
Thương Q(x) = 2x2 – x + 5
Dư R(x) = 2x – 1
Ta có: F(x) = 3x2 . (2x2 – x + 5) + 2x – 1
b)
Thương Q(x) = 4x2 + 2x – 2
Dư R(x) = -x – 1
Ta có: F(x) = (3x2 + x + 1) . (4x2 + 2x – 2) – x – 1
Đúng 0
Bình luận (0)