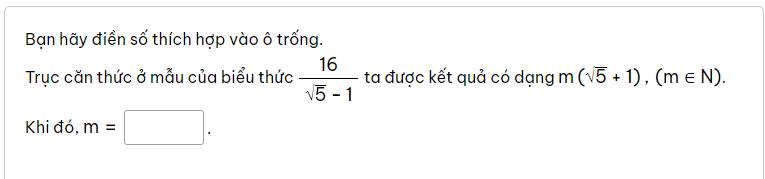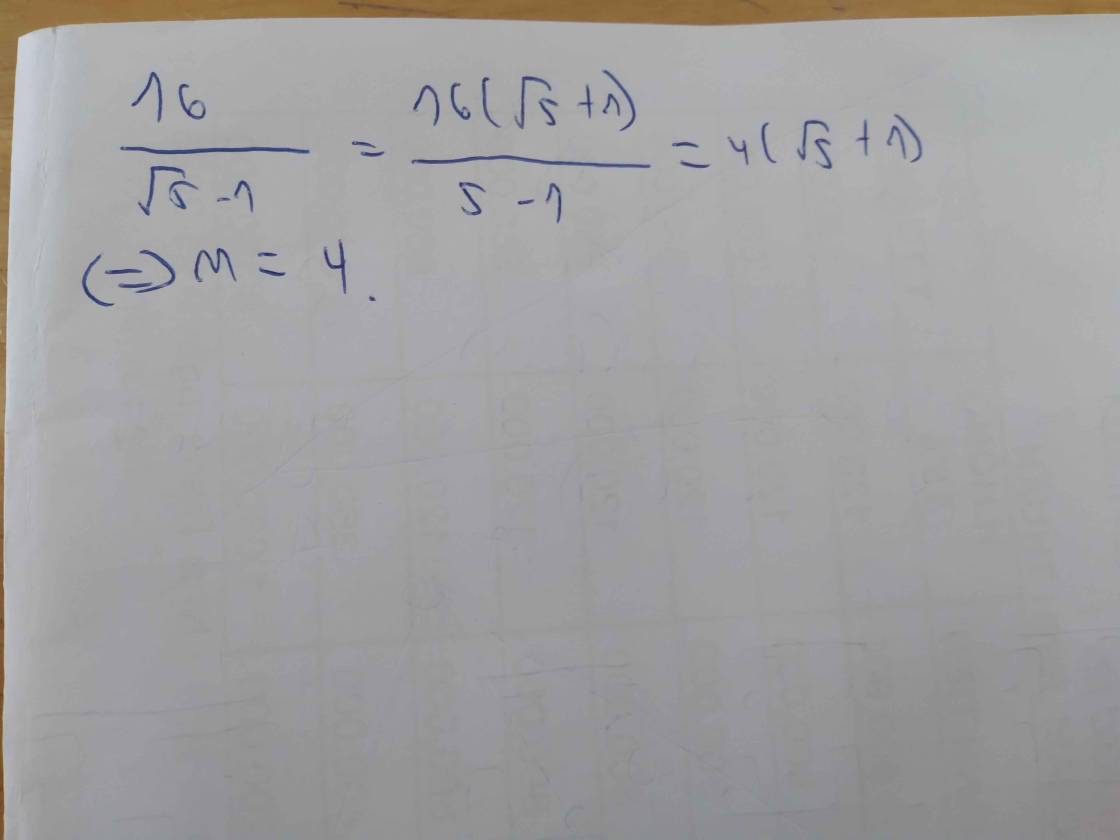
Đề số 1
Ta có:
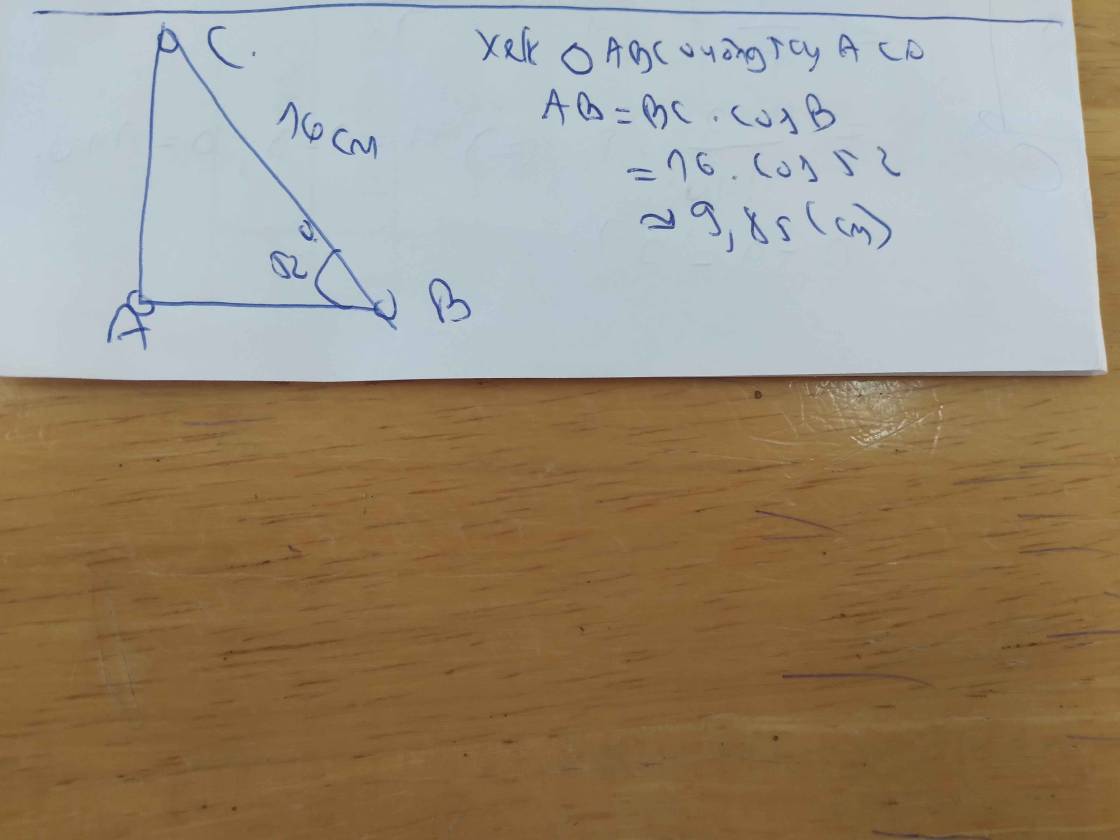
cos ABC = AB/BC
⇒ AB = BC . cos ABC
= 16 . cos 52⁰
≈ 9,85 (cm)
Đúng 2
Bình luận (0)
16/(√5 - 1) = 16(√5 + 1)/(5 - 1)
= 4(√5 + 1)
⇒ m = 4
Đúng 2
Bình luận (0)
Nếu x^2+6x+6/x+1/x^2 hãy tìm giá trị nhỏ nhất
Đề không rõ ràng. Bạn xem lại nhé.
Đúng 0
Bình luận (0)
Đây là những câu em cảm thấy khó đối với các bạn học sinh học tầm trung môn toán trong đợt khảo sát toán lần 2 này nên MỌI NGƯỜI GIÚP EM VỚI Ạ Câu 1 : Tìm giá trị nguyên của m để hai đường thẳng: y2x+4 và yx+m-7 cắt nhau tại điểm A(x;y) thuộc góc phần tư thứ (II) trong mặt phẳng tọa độ Oxy. Câu 2: Cho 2 đường thẳng (d1):y2x+5,(d3): y(m+1)x+2m-1 cắt nhau tại I. Tìm m để đường thẳng (d2): y -4x-1 đi qua điểm I.
Đọc tiếp
Đây là những câu em cảm thấy khó đối với các bạn học sinh học tầm trung môn toán trong đợt khảo sát toán lần 2 này nên MỌI NGƯỜI GIÚP EM VỚI Ạ Câu 1 : Tìm giá trị nguyên của m để hai đường thẳng: y=2x+4 và y=x+m-7 cắt nhau tại điểm A(x;y) thuộc góc phần tư thứ (II) trong mặt phẳng tọa độ Oxy. Câu 2: Cho 2 đường thẳng (d1):y=2x+5,(d3): y=(m+1)x+2m-1 cắt nhau tại I. Tìm m để đường thẳng (d2): y= -4x-1 đi qua điểm I.
Câu 1:
Vì \(2\ne1\)
nên hai đường thẳng y=2x+4 và y=x+m-7 luôn cắt nhau
phương trình hoành độ giao điểm là:
2x+4=x+m-7
=>2x-x=m-7-4
=>x=m-11
Thay x=m-11 vào y=2x+4, ta được:
y=2(m-11)+4=2m-18
=>A(m-11;2m-18)
Để A(m-11;2m-18) thuộc góc phần tư thứ III thì
\(\left\{{}\begin{matrix}m-11< 0\\2m-18< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m< 11\\2m< 18\end{matrix}\right.\)
=>m<9
Câu 2:
Để (d1) và (d3) cắt nhau thì \(m+1\ne2\)
=>\(m\ne1\)
Phương trình hoành độ giao điểm của (d1) và (d2) là:
-4x-1=2x+5
=>-4x-2x=5+1
=>-6x=6
=>x=-1
Thay x=-1 vào y=2x+5, ta được:
y=-2+5=3
Thay x=-1 và y=3 vào (d3), ta được:
-(m+1)+2m-1=3
=>-m-1+2m-1=3
=>m-2=3
=>m=5(nhận)
Đúng 2
Bình luận (0)
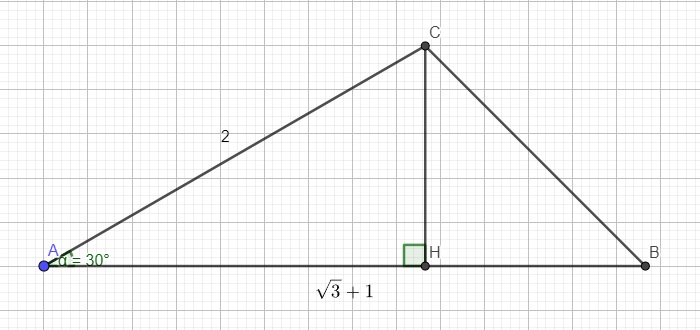
Cho hình tam giác ABC có A^=30°, b=2 và c= căn bậc hai của 3+1, tìm a, B^ và C^
Từ C kẻ CH vuông góc AB
Trong tam giác vuông ACD:
\(CH=AC.sinA=2.sin30^0=1\)
\(AH=AC.cosA=2.cos30^0=\sqrt{3}\)
\(\Rightarrow BH=AB-AH=\sqrt{3}+1-\sqrt{3}=1\)
\(\Rightarrow CH=BH\Rightarrow\Delta BCH\) vuông cân tại H
\(\Rightarrow\widehat{B}=45^0\)
\(a=BC=\sqrt{AH^2+BH^2}=\sqrt{2}\)
\(\widehat{BCH}=45^0\) (do ABH vuông cân)
Trong tam giác vuông ACH:
\(\widehat{ACH}=90^0-\widehat{A}=60^0\)
\(\Rightarrow\widehat{C}=\widehat{ACH}+\widehat{BCH}=105^0\)
Đúng 2
Bình luận (0)
cho đường tròn tâm o bán kính r , từ điểm a nằm ngoài đường tròn vẽ hai tiếp tuyến am , an với đường tròn . i là giao điểm mn và oa . vẽ đường kính mb của đường tròn , qua o kẻ dường thẳng vuông góc với ab tại h , cắt mn tại c , chứng minh bc là tiếp tuyến của đường tròn tâm o , bán kính r
Xét (O) có
AM,AN là các tiếp tuyến
Do đó: AM=AN
=>A nằm trên đường trung trực của MN(1)
Ta có: OM=ON
=>O nằm trên đường trung trực của MN(2)
Từ (1) và (2) suy ra OA là đường trung trực của MN
=>OA\(\perp\)MN tại I
Xét ΔOHA vuông tại H và ΔOIC vuông tại I có
\(\widehat{HOA}\) chung
Do đó: ΔOHA~ΔOIC
=>\(\dfrac{OH}{OI}=\dfrac{OA}{OC}\)
=>\(OH\cdot OC=OA\cdot OI\)
mà \(OA\cdot OI=OM^2=OB^2\)
nên \(OB^2=OH\cdot OC\)
=>\(\dfrac{OB}{OH}=\dfrac{OC}{OB}\)
Xét ΔOBC và ΔOHB có
\(\dfrac{OB}{OH}=\dfrac{OC}{OB}\)
\(\widehat{BOC}\) chung
Do đó: ΔOBC~ΔOHB
=>\(\widehat{OBC}=\widehat{OHB}\)
mà \(\widehat{OHB}=90^0\)
nên \(\widehat{OBC}=90^0\)
=>CB là tiếp tuyến của (O)
Đúng 1
Bình luận (1)
X^-2+3x^-1/x^-2+7x^-1+12
\(\dfrac{x^{-2}+3x^{-1}}{x^{-2}+7x^{-1}+12}\)
\(=\left(\dfrac{1}{x^2}+\dfrac{3}{x}\right):\left(\dfrac{1}{x^2}+\dfrac{7}{x}+12\right)\)
\(=\dfrac{1+3x}{x^2}:\dfrac{1+7x+12x^2}{x^2}\)
\(=\dfrac{1+3x}{1+7x+12x^2}\)
\(=\dfrac{3x+1}{12x^2+3x+4x+1}\)
\(=\dfrac{3x+1}{3x\left(4x+1\right)+\left(4x+1\right)}=\dfrac{1}{4x+1}\)
Đúng 2
Bình luận (0)