Cho K=|x -\(\dfrac{1}{2}\)|+ \(\dfrac{3}{4}\) -x. Tìm GTNN, GTLN của K
Cho biểu thức: K=(\(\dfrac{x^2}{x^2-5x+6}\)+\(\dfrac{x^2}{x^2-3x+2}\)).\(\dfrac{\left(x-1\right)\left(x-3\right)}{x^4+x^2+1}\)
a, Tìm đkxđ rồi rút gọn K
b, Tìm GTLN của K
a: ĐKXĐ: x<>1; x<>2; x<>3
\(K=\left(\dfrac{x^2}{\left(x-2\right)\left(x-3\right)}+\dfrac{x^2}{\left(x-1\right)\left(x-2\right)}\right)\cdot\dfrac{\left(x-1\right)\left(x-3\right)}{x^4+2x^2+1-x^2}\)
\(=\dfrac{x^3-x^2+x^3-3x^2}{\left(x-2\right)\left(x-3\right)\left(x-1\right)}\cdot\dfrac{\left(x-1\right)\left(x-3\right)}{\left(x^2+1+x\right)\left(x^2+1-x\right)}\)
\(=\dfrac{2x^3-4x^2}{\left(x-2\right)}\cdot\dfrac{1}{\left(x^2+x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{2x^2\left(x-2\right)}{\left(x-2\right)\left(x^4+x^2+1\right)}=\dfrac{2x^2}{x^4+x^2+1}\)
b:
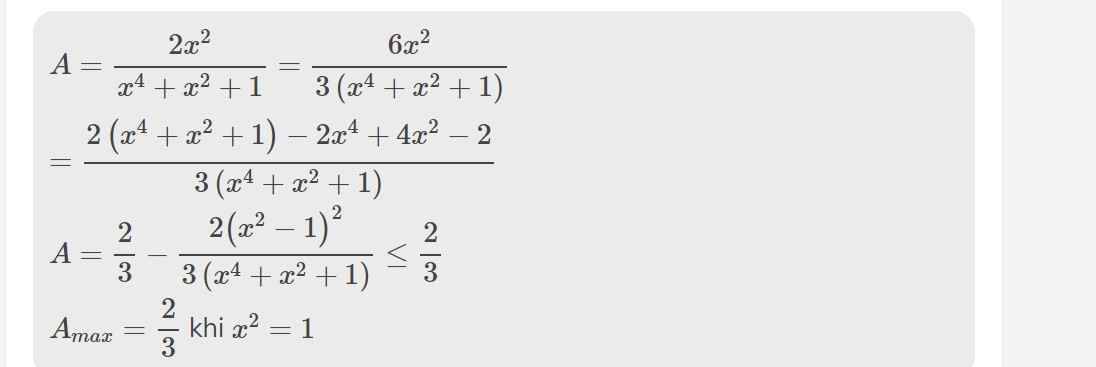
1. Tìm GTNN của \(y=x+\dfrac{1}{x}-5\) trên \(\left(0,+\infty\right)\)
2. Tìm GTNN của \(y=4x^2+\dfrac{1}{x}-4\) trên \(\left(0,+\infty\right)\)
3. Tìm GTLN của \(y=\dfrac{x^2+4}{x}\) trên \(\left(-\infty,0\right)\)
\(y=x+\dfrac{1}{x}-5\ge2\sqrt{\dfrac{x}{x}}-5=-3\)
\(y_{min}=-3\) khi \(x=1\)
\(y=4x^2+\dfrac{1}{2x}+\dfrac{1}{2x}-4\ge3\sqrt[3]{\dfrac{4x^2}{2x.2x}}-4=-1\)
\(y_{min}=-1\) khi \(x=\dfrac{1}{2}\)
\(y=x+\dfrac{4}{x}\Rightarrow y'=1-\dfrac{4}{x^2}=0\Rightarrow x=-2\)
\(y\left(-2\right)=-4\Rightarrow\max\limits_{x>0}y=-4\) khi \(x=-2\)
1. tìm GTNN của A= x(x+2)(x+4)(x+6)+8
2. tìm GTLN của B=5+(1-x)(x+2)(x+3)(x+6)3
3.tìm GTNN của C=(x+3)4 + (x-7)4
4. Cho x>0. Tìm GTNN của P=\(\dfrac{4x^2+1}{2x}\)
1.
$x(x+2)(x+4)(x+6)+8$
$=x(x+6)(x+2)(x+4)+8=(x^2+6x)(x^2+6x+8)+8$
$=a(a+8)+8$ (đặt $x^2+6x=a$)
$=a^2+8a+8=(a+4)^2-8=(x^2+6x+4)^2-8\geq -8$
Vậy $A_{\min}=-8$ khi $x^2+6x+4=0\Leftrightarrow x=-3\pm \sqrt{5}$
2.
$B=5+(1-x)(x+2)(x+3)(x+6)=5-(x-1)(x+6)(x+2)(x+3)$
$=5-(x^2+5x-6)(x^2+5x+6)$
$=5-[(x^2+5x)^2-6^2]$
$=41-(x^2+5x)^2\leq 41$
Vậy $B_{\max}=41$. Giá trị này đạt tại $x^2+5x=0\Leftrightarrow x=0$ hoặc $x=-5$
3.
Đặt $x+3=a; 7-x=b$ thì $a+b=10$
$C=a^4+b^4$
Áp dụng BĐT Bunhiacopxky:
$(a^4+b^4)(1+1)\geq (a^2+b^2)^2$
$\Rightarrow C\geq \frac{(a^2+b^2)^2}{2}$
$(a^2+b^2)(1+1)\geq (a+b)^2=100$
$\Rightarrow a^2+b^2\geq 50$
$\Rightarrow C\geq \frac{50^2}{2}=1250$
Vậy $C_{\min}=1250$
Giá trị này đạt tại $a=b=5\Leftrightarrow x=2$
a) Tìm GTNN Của:
A=\(\left(2x+\dfrac{1}{3}\right)^4-1\)
a) Tìm GTLN Của:
B=\(-\left(\dfrac{4}{9}x-\dfrac{2}{15}\right)^6+3\)
\(B=-\left(\dfrac{4}{9}x-\dfrac{2}{15}\right)^6+3\)
vì \(B=-\left(\dfrac{4}{9}x-\dfrac{2}{15}\right)^6\le0,\forall x\inℝ\)
\(\Rightarrow B=-\left(\dfrac{4}{9}x-\dfrac{2}{15}\right)^6+3\le3\)
Dấu "=" xảy ra khi và chỉ khi
\(\dfrac{4}{9}x-\dfrac{2}{15}=0\Rightarrow\dfrac{4}{9}x=\dfrac{2}{15}\Rightarrow x=\dfrac{9}{15}\)
Vậy \(GTLN\left(B\right)=3\left(tạix=\dfrac{9}{15}\right)\)
\(A=\left(2x+\dfrac{1}{3}\right)^4-1\)
vì \(\left(2x+\dfrac{1}{3}\right)^4\ge0,\forall x\inℝ\)
\(\Rightarrow A=\left(2x+\dfrac{1}{3}\right)^4-1\ge-1\)
Dấu "=" xảy ra khi và chỉ khi
\(2x+\dfrac{1}{3}=0\Rightarrow2x=-\dfrac{1}{3}\Rightarrow x=-\dfrac{1}{6}\)
\(\Rightarrow GTNN\left(A\right)=-1\left(tạix=-\dfrac{1}{6}\right)\)
tìm gtln gtnn của:
\(A=\left|x+1\right|-3\)
\(B=-\left|x-\dfrac{3}{7}\right|-\dfrac{1}{4}\)
\(A=\left|x+1\right|-3\\ min_A=-3.khi.x+1=0\Leftrightarrow x=-1\\ B=-\left|x-\dfrac{3}{7}\right|-\dfrac{1}{4}\\ max_B=-\dfrac{1}{4}.khi.\left(x-\dfrac{3}{7}\right)=0\Leftrightarrow x=\dfrac{3}{7}\)
a)
A = |x + 1| - 3 ≥ 0 - 3 = -3
Dấu "=" xảy ra khi x + 1 = 0 hay x = -1
Do đó A đạt GTNN là -3 khi x = -1
b)
\(B=-\left|x-\dfrac{3}{7}\right|-\dfrac{1}{4}\le-0-\dfrac{1}{4}=-\dfrac{1}{4}\)
Dấu "=" xảy ra khi khi \(x-\dfrac{3}{7}=0\) hay \(x=\dfrac{3}{7}\)
Do đó B đạt GTLN là \(-\dfrac{1}{4}\) khi \(x=\dfrac{3}{7}\)
\(\dfrac{1}{2x-x^2-4}\) tìm GTLN/ GTNN
\(\dfrac{3x^2+14}{x^2+4}\)
\(\dfrac{2x+1}{x^2+2}\)
Cho \(x\ge0\).Tìm GTNN của biểu thức :
K = \(\dfrac{x+\sqrt{x}+4}{\sqrt{x}+1}\)
Lời giải:
$K=\frac{\sqrt{x}(\sqrt{x}+1)+4}{\sqrt{x}+1}=\sqrt{x}+\frac{4}{\sqrt{x}+1}$
$=(\sqrt{x}+1)+\frac{4}{\sqrt{x}+1}-1$
$\geq 2\sqrt{4}-1=3$ (theo BĐT Cô-si)
Vậy $K_{\min}=3$. Giá trị này đạt tại $\sqrt{x}+1=2\Leftrightarrow x=1$
Tìm GTNN của các biểu thức sau:
1) G= \(\dfrac{x^2}{x-1}\)với x>1
2) H= \(x+\dfrac{1}{x}\)với x ≥2
3) K= \(x^2+\dfrac{1}{x}\)với x ≥3
G = \(\dfrac{x^2}{x-1}\)
= \(\dfrac{x^2-4x+4+4x-4}{x-1}\)
= \(\dfrac{\left(x-2\right)^2+4\left(x-1\right)}{x-1}\)
= \(\dfrac{\left(x-2\right)^2}{x-1}+4\)
Vì x>1 nên \(\left\{{}\begin{matrix}\left(x-2\right)^2\text{≥}0\\x-1>0\end{matrix}\right.\)
=> G ≥ 4
=> G = 4 đạt GTNN
Dấu bằng xảy ra <=> \(\left(x-2\right)^2=0\)
<=> \(x=2\)
\(Do\) \(x>2\)
\(=>\left\{{}\begin{matrix}x-2\text{ ≥0}\\2x-1>0\end{matrix}\right.\)
\(=>\left(x-2\right)\left(2x-1\right)\text{ ≥0}\)
\(< =>2x^2-5x+2\text{≥}0\)
\(< =>2x^2+2\text{≥}5x\)
\(< =>2x+\dfrac{2}{x}\text{≥}5\)
\(< =>x+\dfrac{1}{x}\text{≥}2,5\)
\(< =>H\text{≥}2,5\)
\(< =>H=5\) \(đạt\) \(GTNN\)
Dấu bằng xảy ra khi \(x-2=0< =>x=2\)
\(K=x^2+\dfrac{1}{x}\)
\(=\dfrac{53x^3}{54}+\left(\dfrac{x^2}{54}+\dfrac{1}{2x}+\dfrac{1}{2x}\right)\)
Áp dụng BĐT Cô si cho 3 số dương
\(\dfrac{x^2}{54}+\dfrac{1}{2x}+\dfrac{1}{2x}\text{≥}3.\sqrt[3]{\dfrac{x^2}{54}.\dfrac{1}{2x}.\dfrac{1}{2x}}\)\(\text{≥}\dfrac{53.9}{54}+3.\sqrt[3]{54.4}\)\(=\dfrac{28}{3}\)
Dấu bằng xảy ra khi \(\left\{{}\begin{matrix}\dfrac{x^2}{54}=\dfrac{1}{2x}=\dfrac{1}{2x}\\x=3\end{matrix}\right.\)\(< =>x=3\)
Tìm GTLN, GTNN của \(P=\dfrac{x+4}{4\sqrt{x}}\)
Tìm GTLN, GTNN của \(P=\dfrac{x+3}{2\left(\sqrt{x}+1\right)}\) (x ≥ 0)
Tìm GTNN, GTLN của \(P=\dfrac{x-4}{\sqrt{x}+1}\)
Tất cả 3 bài này đều chung một dạng, bậc tử lớn hơn bậc mẫu nên đều không tồn tại GTLN mà chỉ tồn tại GTNN. Cách tìm thường là chia tử cho mẫu rồi khéo léo thêm bớt để sử dụng BĐT Cô-si
a) \(P=\dfrac{x+4}{4\sqrt{x}}=\dfrac{\sqrt{x}}{4}+\dfrac{1}{\sqrt{x}}\ge2\sqrt{\dfrac{\sqrt{x}}{4}\dfrac{1}{\sqrt{x}}}=2.\dfrac{1}{2}=1\)
\(\Rightarrow P_{min}=1\) khi \(\dfrac{\sqrt{x}}{4}=\dfrac{1}{\sqrt{x}}\Leftrightarrow x=4\)
b) \(P=\dfrac{x+3}{2\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}-1}{2}+\dfrac{2}{\sqrt{x}+1}=\dfrac{\sqrt{x}+1}{2}+\dfrac{2}{\sqrt{x}+1}-1\)
\(\Rightarrow P\ge2\sqrt{\dfrac{\left(\sqrt{x}+1\right)}{2}\dfrac{2}{\left(\sqrt{x}+1\right)}}-1=2-1=1\)
\(\Rightarrow P_{min}=1\) khi \(\dfrac{\sqrt{x}+1}{2}=\dfrac{2}{\sqrt{x}+1}\Leftrightarrow x=1\)
c)ĐKXĐ: \(x\ge0\Rightarrow\) \(P=\dfrac{x-4}{\sqrt{x}+1}=\sqrt{x}-1-\dfrac{3}{\sqrt{x}+1}\)
\(P_{min}\) khi \(\dfrac{3}{\sqrt{x}+1}\) đạt max \(\Rightarrow\sqrt{x}+1\) đạt min, mà \(\sqrt{x}+1\ge1\) \(\forall x\ge0\) , dấu "=" xảy ra khi \(x=0\)
\(\Rightarrow P_{min}=-4\) khi \(x=0\)