Gọi \(A\left(x;y\right)\). Do \(A,B\in\left(E\right)\) có hoành độ dương và tam giác \(OAB\) cân tại \(O\), nên:

\(B\left(x;y\right),x>0.=>AB=2\left|y\right|=\sqrt{4-x^2}\)

Gọi \(H\) là trung điểm \(AB,\)  ta có: \(OH\pm AB\) và \(OH=x\).

Diện tích: \(S_{OAB}=\frac{1}{2}x\sqrt{4-x^2}\)

                          \(=\frac{1}{2}\sqrt{x^2\left(4-x^2\right)\le1}\)

Dấu " = "  xảy ra, khi và chỉ khi \(x=\sqrt{2}\)

Vậy: \(A\left(\sqrt{2};\frac{\sqrt{2}}{2}\right)\) và \(B\left(\sqrt{2};-\frac{\sqrt{2}}{2}\right)\) hoặc \(A\left(\sqrt{2};-\frac{\sqrt{2}}{2}\right)\) và \(B\left(\sqrt{2};\frac{\sqrt{2}}{2}\right)\).

Phương trình chính tắc của \(\left(E\right)\) có dạng: \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\), với \(a>b>0\) và \(2a=8=>a=4\).

Do \(\left(E\right)\) và \(\left(C\right)\) cùng nhận \(Ox\) và \(Oy\) làm trục đối xứng và các giao điểm là các đỉnh của một hình vuông nên \(\left(E\right)\) và \(\left(C\right)\) có một giao điểm với tọa độ dạng \(A\left(t;t\right),t>0\)

\(A\in\left(C\right)\Leftrightarrow t^2+t^2=8=>t=2\)

\(A\left(2;2\right)\in\left(E\right)\Leftrightarrow\frac{4}{16}+\frac{4}{b^2}=1\Leftrightarrow b^2=\frac{16}{3}\)

Phương trình chính tắc của \(\left(E\right)\) là \(\frac{x^2}{16}+\frac{y^2}{\frac{16}{3}}=1\) 

hhu99cuoo[cjropjp4h

a, Ta có: BE song song AC ( theo bài ra)

               AB song song CE ( E thuộc CD)

       nên ABEC là hình bình hành, do đó AC=BE

               mà AC = BD

         nên BD=BE do đó BDE là tam giác cân

b, Ta có AC song song BE nên ˆBEC=ˆACD

        mà ˆBED=ˆBDC ( BDE là tam giác cân )

                       do đó  ˆACD=ˆBDC

      Xét tg ACD và tg BDC có : ˆACD=ˆBDC

                                                AC=BD( theo gt )

                                                BC là cạnh chung

        nên tg ACD =tg BDC ( c-g-c)

c, Theo chứng minh câu b, ta có: tg ACD= tg BDC

              do đó ˆADC=ˆBCD

        Vậy ABCD là hình thang cân

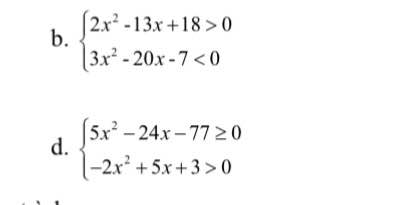
b.

\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x< 2\\x>\dfrac{9}{2}\end{matrix}\right.\\-\dfrac{1}{3}< x< 7\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}-\dfrac{1}{3}< x< 2\\\dfrac{9}{2}< x< 7\end{matrix}\right.\)

Hay \(S=\left(-\dfrac{1}{3};2\right);\left(\dfrac{9}{2};7\right)\)

d.

\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\le-\dfrac{11}{5}\\x\ge7\end{matrix}\right.\\-\dfrac{1}{2}< x< 3\end{matrix}\right.\) \(\Rightarrow x\in\varnothing\) hay BPT vô nghiệm

Bài 4: 

a: Xét tứ giác OBAC có 

\(\widehat{OBA}+\widehat{OCA}=180^0\)

Do đó: OBAC là tứ giác nội tiếp

hay O,B,A,C cùng thuộc 1 đường tròn

Bài 5:

\(\sqrt{x+2021}-y^3=\sqrt{y+2021}-x^3\\ \Leftrightarrow\left(\sqrt{x+2021}-\sqrt{y+2021}\right)+\left(x^3-y^3\right)=0\\ \Leftrightarrow\dfrac{x-y}{\sqrt{x+2021}+\sqrt{y+2021}}+\left(x-y\right)\left(x^2+xy+y^2\right)=0\\ \Leftrightarrow\left(x-y\right)\left(\dfrac{1}{\sqrt{x+2021}+\sqrt{y+2021}}+x^2+xy+y^2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-y=0\\\dfrac{1}{\sqrt{x+2021}+\sqrt{y+2021}}+x^2+xy+y^2=0\left(1\right)\end{matrix}\right.\)

Dễ thấy \(\left(1\right)>0\) với mọi x,y

Do đó \(x-y=0\) hay \(x=y\)

\(\Leftrightarrow M=x^2+2x^2-2x^2+2x+2022=x^2+2x+1+2021\\ \Leftrightarrow M=\left(x+1\right)^2+2021\ge2021\)

Dấu \("="\Leftrightarrow x=y=-1\)

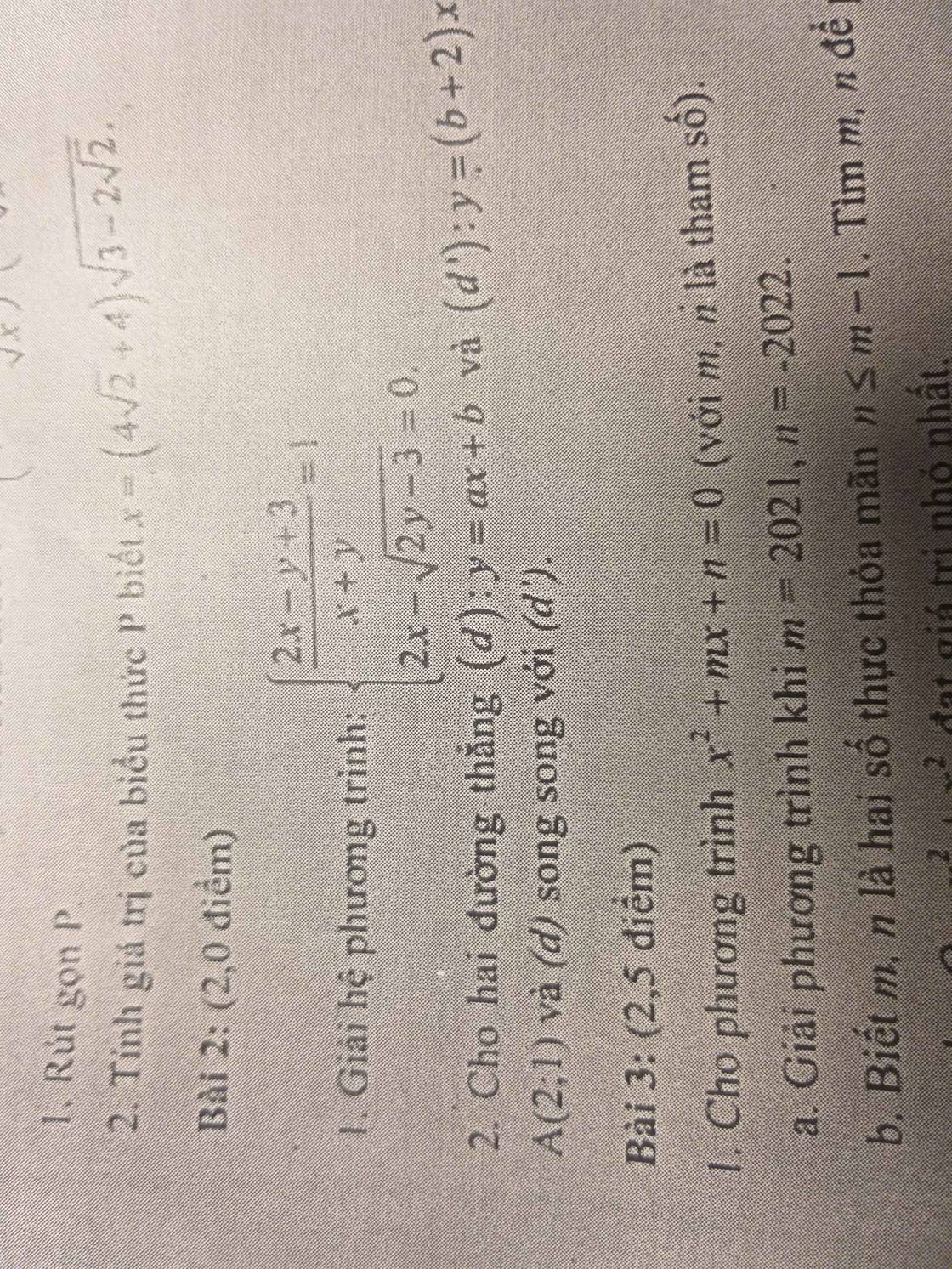
ĐK: \(\left\{{}\begin{matrix}x\ne-y\\y\ge\dfrac{3}{2}\end{matrix}\right.\).

\(\left\{{}\begin{matrix}\dfrac{2x-y+3}{x+y}=1\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2x-y+3}{x+y}-1=0\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2x-y+3}{x+y}-\dfrac{x+y}{x+y}=0\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-y+3-x-y=0\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-2y+3=0\\2x-\sqrt{2y-3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-\left(2y-3\right)=0\\2x-\sqrt{2y-3}=0\end{matrix}\right..\)

Đặt a = x, b = \(\sqrt{2y-3}\).

Hệ phương trình trở thành: \(\left\{{}\begin{matrix}a-b^2=0\\2a-b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=b^2\\2b^2-b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=b^2\\b\left(2b-1\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=b^2\\\left[{}\begin{matrix}b=0\\b=\dfrac{1}{2}\end{matrix}\right.\end{matrix}\right.\left\{{}\begin{matrix}\left[{}\begin{matrix}a=0\\a=\dfrac{1}{4}\end{matrix}\right.\\\left[{}\begin{matrix}b=0\\b=\dfrac{1}{2}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=0\\x=\dfrac{1}{4}\end{matrix}\right.\\\left[{}\begin{matrix}y=\dfrac{3}{2}\\2y-3=\dfrac{1}{4}\end{matrix}\right.\end{matrix}\right.\left\{{}\begin{matrix}\left[{}\begin{matrix}x=0\\x=\dfrac{1}{4}\end{matrix}\right.\\\left[{}\begin{matrix}y=\dfrac{3}{2}\\2y=\dfrac{13}{4}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=0\\x=\dfrac{1}{4}\end{matrix}\right.\\\left[{}\begin{matrix}y=\dfrac{3}{2}\\y=\dfrac{13}{8}\end{matrix}\right.\end{matrix}\right..\)

Vậy hệ phương trình có nghiệm (x;y) \(\in\) \(\left\{\left(0;\dfrac{3}{2}\right),\left(\dfrac{1}{4};\dfrac{13}{8}\right)\right\}\).

P6:

1. big

2. been

3. bought

4. people

P7:

1. T

2. F

3. F

4. F

\(=\left(x-y\right)^2-9=\left(x-y-3\right)\left(x-y+3\right)\)

\(x^2-2xy-9+y^2=\left(x^2-2xy+y^2\right)-9=\left(x-y\right)^2-3^2=\left(x-y-3\right).\left(x-y+3\right)\)

\(x^2-2xy-9+y^2=x^2-2xy+y^2-9=\left(x^2-2xy+y^2\right)-9=\left(x-y\right)^2-9=\left(x-y-3\right).\left(x-y+3\right)\)

jimmmmmmmmmmmmmmmmmmmmmmmmmmm

he he he he he he

bài 1:

bn lấy giá trị của √(4^2-3,9^2) là dc

bài 2

AB+BC=2√(3^2+4^2)=??