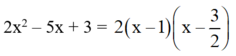Cho Q(x) = ax2+bx+c (a;b;c \(\in\) Z )
Biết Q(x) chia hết ch0 2014 với mọi x \(\in Z\)
Chứng minh rằng : 3a + 5b +7c chia hết cho 1007
a, Chứng tỏ rằng nếu a + b + c = 0 thì x = 1 là một nghiệm của đa thức P(x) = ax2 + bx + c
b, Chứng tỏ rằng nếu a – b + c = 0 thì x = -1 là một nghiệm của đa thức Q(x) = ax2 + bx + c
$\rm x=1\\\to ax^2+bx+c=a+b+c=0\\\to x=1\,\là \,\,no \,\pt$
cho phương trình ax2 + bx + c = 0 vô nghiệm ( a>0)
CMR: ax2 + bx + c > 0 với mọi x thuộc R
Vì PTVN nên Δ<0
=>f(x)=ax^2+bx+c luôn cùng dấu với a
=>f(x)>0 với mọi x
Tìm hệ số a,b,c biết
a, −3x2(2ax2−bx+c)=6x5+9x4−3c2∀x−3x2(2ax2−bx+c)=6x5+9x4−3c2∀x
b,(x2+cx+2)(a+b)=x3+x2−2∀x(x2+cx+2)(a+b)=x3+x2−2∀x
c,(ax2+bx+c)+(x+3)=x2+2x−3x∀x(ax2+bx+c)+(x+3)=x2+2x−3x∀x
Help me!!
bạn ghi lại đề đi mình chả hiểu cái mô tê gì cả
Cho Q(x) = ax2+bx+c (a;b;c ∈ ∈ Z ). Biết Q(x) chia hết ch0 2014 với mọi x ∈Z ∈ Z. Chứng minh rằng : 3a + 5b +7c chia hết cho 1007.
\(Q\left(0\right)=c⋮2014⋮1007\)
\(Q\left(1\right)=\left(a+b+c\right)⋮2014\Rightarrow\left(a+b\right)⋮2014\Rightarrow\left(2a+2b\right)⋮2014\)
\(Q\left(2\right)=\left(4a+2b+c\right)⋮2014\Rightarrow\left(4a+2b\right)⋮2014\)
\(\Rightarrow\left(4a+2b-2a-2b\right)⋮2014\)
\(\Rightarrow2a⋮2014\Rightarrow a⋮1007\Rightarrow b⋮1007\)
\(\Rightarrowđpcm\)
cho đa thức K(x) = P(x) + Q(x) + ax2 + bx + c. tìm a,b,c biết rằng: K(0)=3, K(1)=12 và K(-1)=6
Cho Q(x)=ax2+bx+c. Chứng minh rằng Q(1).Q(2) là 1 số không dương biết 2a+c=0
tìm điều kiện của a,b,c để phương trình sau vô nghiệm:
a(ax2+bx+c)2+b(ax2+bx+c)+c=x
Chứng tỏ rằng nếu phương trình a x 2 + b x + c = 0 có nghiệm là x 1 v à x 2 thì tam thức a x 2 + b x + c phân tích được thành nhân tử như sau:
a x 2 + b x + c = a ( x - x 1 ) ( x - x 2 )
Áp dụng : phân tích đa thức thành nhân tử.
a ) 2 x 2 - 5 x + 3 ; b ) 3 x 2 + 8 x + 2
* Chứng minh:
Phương trình a x 2 + b x + c = 0 có hai nghiệm x 1 ; x 2
⇒ Theo định lý Vi-et: 
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 
= a . x 2 + b x + c ( đ p c m ) .
* Áp dụng:
a) 2 x 2 – 5 x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm 
Vậy: 
b) 3 x 2 + 8 x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ ’ = 4 2 – 2 . 3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:

Chứng tỏ rằng nếu phương trình ax2 + bx + c = 0 có nghiệm là x1 và x2 thì tam thức ax2 + bx + c phân tích được thành nhân tử như sau:
ax2 + bx + c = a( x - x1)(x - x2)
Áp dụng : phân tích đa thức thành nhân tử.
3x2 + 8x + 2
3x2 + 8x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ’ = 42 – 2.3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:

Chứng tỏ rằng nếu phương trình ax2 + bx + c = 0 có nghiệm là x1 và x2 thì tam thức ax2 + bx + c phân tích được thành nhân tử như sau:
ax2 + bx + c = a( x - x1)(x - x2)
Áp dụng : phân tích đa thức thành nhân tử.
2x2 - 5x + 3
* Chứng minh:
Phương trình ax2 + bx + c = 0 có hai nghiệm x1; x2
⇒ Theo định lý Vi-et: 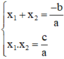
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 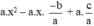
= a.x2 + bx + c (đpcm).
* Áp dụng:
a) 2x2 – 5x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm 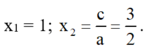
Vậy: