Cho hàm số: \(y=f\left(x\right)=x^2.\)
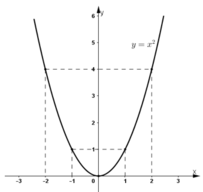
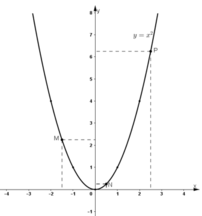
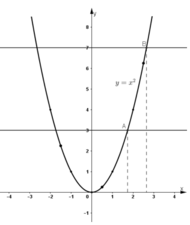
a) Vẽ đồ thị của hàm số đó.
b) Tính các giá trị f(-8); f(-1;3); f(-0,75); f(1,5).
c) Dùng đồ thị để ước lượng các giá trị (0,5)2; (-1,5)2; (2,5)2.
d) Dùng đồ thị để ước lượng vị trí các điểm trên trục hoành biểu diễn các số \(\sqrt{3};\sqrt{7}.\)


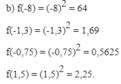


 9 đko nhỉ
9 đko nhỉ