cho hình bình hành ABCD. Biết AB//CD và AC // BD chứng minh rằng AB=CD và AC=BD
NL
Những câu hỏi liên quan
Cho hình bình hành ABCD có AB=2BC. Gọi M và N là Trung điểm của AB, CD. a) chứng minh rằng AMND là hình thoi. b)chứng minh rằng MBND là hình bình hành. C) chứng minh rằng AC, BD, MN đồng quy
Cho hình bình hành ABCD có BC = AC. Gọi I là trung điểm cạnh CD, M là giao của BD và AI;
N là giao của AB và CM. Chứng minh rằng CN = BD
Cho hình thang ABCD (AB // CD). Gọi M, N, P, Q theo thứ tự là trung điểm của AB, AC, CD, BD. Chứng minh rằng MNPQ là hình bình hành.
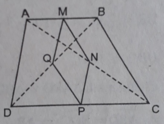
MN // QP (cùng song song với BC)
MN = QP ( =1/2 BC)
⇒ MNPQ là hình bình hành.
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Chứng minh rằng
\(AB^2+BC^2+CD^2+DA^2=AC^2+BD^2\)
Cho hình bình hành ABCD (AB>AD) gọi E và K lần lượt là trung điểm của CD và AB, BD cắt AC tại O chứng minh rằng :
a, Tứ giác AECK là hình bình hành
b, ba điểm E,O,K thẳng hàng
a) Ta có: \(AB=DC,AB//CD\)(ABCD là hình bình hành)
Mà \(K,E\in AB,CD;AK=\dfrac{1}{2}AB;CE=\dfrac{1}{2}CD\)
\(\Rightarrow AK=CE\) và \(AK//CE\)
=> AECK là hình bình hành
b) Ta có: O là giao điểm 2 đường chéo AC và BD
=> O là trung điểm AC
=> O là trung điểm KE(AECK là hình bình hành)
=> E,O,K thẳng hàng
Đúng 1
Bình luận (0)
1. Cho hình thang ABCD có góc A góc D 90 độ , đáy nhỏ AB a , cạnh bên BC 2 a . Gọi M , N lần lượt là trung điểm AD , ABa / Tính số đo các góc ABC , BANb/ Chứng minh tam giác NAD đềuc/ Tính MN theo a 2. a/ Tính các góc A , góc B của hình thang ABCD ( AB // CD ) biết góc C 70 độ , góc D 40 độb/ Cho hình thang ABCD có AB // CD và góc A góc D . Chứng minh rằng ABCD là hình thang vuông cà AC^2 + BD^2 AB^2 + CD^2 + 2AD^23. Cho tứ giác ABCD :a/ Chứng minh rằng AB + CD AC + BDb/ Cho biết AB + B...
Đọc tiếp
1. Cho hình thang ABCD có góc A = góc D = 90 độ , đáy nhỏ AB = a , cạnh bên BC = 2 a . Gọi M , N lần lượt là trung điểm AD , AB
a / Tính số đo các góc ABC , BAN
b/ Chứng minh tam giác NAD đều
c/ Tính MN theo a
2. a/ Tính các góc A , góc B của hình thang ABCD ( AB // CD ) biết góc C = 70 độ , góc D = 40 độ
b/ Cho hình thang ABCD có AB // CD và góc A = góc D . Chứng minh rằng ABCD là hình thang vuông cà AC^2 + BD^2 = AB^2 + CD^2 + 2AD^2
3. Cho tứ giác ABCD :
a/ Chứng minh rằng AB + CD < AC + BD
b/ Cho biết AB + BD < hoặc = AC + CD
Chứng minh rằng AB < AC
4. Cho hình thang ABCD có AC vuông góc BD . CHứng minh rằng :
a/ AB^2 + CD^2 = AD^2 + BC^2
b/ ( AB + CD )^2 = AC^2 + BD^2
bạn hỏi thế này thì chả ai muốn làm -_- dài quá
Đúng 1
Bình luận (0)
Bạn gửi từng câu nhò thì các bạn khác dễ làm hơn!
Đúng 1
Bình luận (0)
dài quà làm sao mà có thòi gian mà trả lời .bạn hỏi ít thoi chứ
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Chọn hình thang ABCD ( AB // CD )
a) Biết DAB - ADC = 60 độ. Tính ADC
b) Gọi O là giao điểm của AC và BD. Biết OA = OB. Chứng minh ABCD là hình bình hành
a: AB//CD
=>\(\widehat{DAB}+\widehat{ADC}=180^0\)
mà \(\widehat{DAB}-\widehat{ADC}=60^0\)
nên \(\widehat{ADC}=\dfrac{180^0-60^0}{2}=60^0\)
b: Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)
\(\widehat{AOB}=\widehat{COD}\)
Do đó: ΔOAB đồng dạng với ΔOCD
=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
=>OC=OD
OA+OC=AC
OB+OD=BD
mà OA=OB và OC=OD
nên AC=BD
=>ABCD chỉ là hình thang cân thôi chứ không là hình bình hành nha bạn
Đúng 1
Bình luận (0)
Cho ABCD là hình bình hành. Lấy E và F trên AB và CD sao cho AE = FC
a) Chứng minh AECF là hình bình hành.
b) Chứng minh BE = FD.
c) Chứng minh DEBF là hình bình hành.
d) Chứng minh AC; BD và EF đồng quy.
a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
b: Ta có: AE+BE=AB
FC+FD=CD
mà AB=CD
và AE=CF
nên BE=FD
Đúng 1
Bình luận (0)
Cho ABCD là hình bình hành. Lấy E và F trên AB và CD sao cho AE = FC.
a) Chứng minh AECF là hình bình hành.
b) Chứng minh BE = FD.
c) Chứng minh DEBF là hình bình hành.
d) Chứng minh AC; BD và EF đồng quy.
\(a,\left\{{}\begin{matrix}AE=FC\\AE//FC\left(AB//CD\right)\end{matrix}\right.\Rightarrow AECF\) là hbh
\(b,AE=CF\left(gt\right);AB=CD\left(hbh.ABCD\right)\\ \Rightarrow AB-AE=CD-CF\\ \Rightarrow BE=FD\)
\(c,\left\{{}\begin{matrix}BE=FD\left(cm.trên\right)\\BE//FD\left(AB//CD\right)\end{matrix}\right.\Rightarrow DEBF\) là hbh
\(d,\) Gọi M là giao AC và BD
Mà ABCD là hbh nên M là trung điểm AC,BD
Mà DEBF là hbh, M là trung điểm BD nên cũng là trung điểm EF
Do đó AC,BD,EF đồng quy tại M
Đúng 3
Bình luận (0)





