Các câu hỏi tương tự
Cho hình vẽ biết AB // CD và AD // BC (nó như là hình bình hành ấy, AB và DC là chiều dài)
a) CMR: AB = CD và AD = BC
b) Gọi O là giao điểm của AC và BD, chứng minh O là trung điểm của AC và BD
LD
30 tháng 4 2020 lúc 20:09
Cho hình thang ABCD có AB // CD . Biết rằng ( AB + CD )2 = AC2 + BD2 . Chứng minh rằng BD vuông góc với AC
Cho đoạn thẳng AB. Vẽ về hai phía của các đoạn thẳng AB, AC vuông góc với AB sao cho AC = BD
a)Chứng minh ACBD là hình bình hành
b) Lấy E thuộc AC; F thuộc BD sao cho AE =BF. Gọi giao điểm của AB và CD là I. Chúng minh E, I, F thẳng hàng.
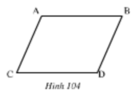
Trên hình 104 ta có AB // CD, AC // BD. Hãy chứng minh rằng AB = CD, AC = BD.
Cho hình bình hành ABCD. Phía trong hình bình hành dựng các tia Ax, By, Cz, Dt theo thứ tự tạo với các cạnh AB, BC, CD, DA.Các goc bằng nhau và cắt nhau tại M,N,P,Q
Chứng minh: a, MNPQ là hình bình hành
b, MP, NQ, AC, BD đồng quy
cho tứ giác ABCD . gọi O là giao điểm của hai đường chéo AC và BD . Chứng minh :
a) AC+BD>AB+CD
b)AC+BD>AD+ BC
Cho hình thang ABCD có đáy AB > đáy CD và hai đường chéo AC và BD vuông
góc. Trên đáy AB lấy M sao cho AM có độ dài bằng đường trung bình của hình thang
ABCD. Chứng minh : CA là đường phân giác góc MCD
TK
18 tháng 9 2021 lúc 9:17
cho hình thang cân ABCD có ab//cd và ab<cd. kẻ đường cao ah và bk. gọi O là giao điểm của ac và bd; i là giao điểm ad và bc. Chứng minh OI là trung trực AB.
Cho 2 đoạn AB và CD cắt nhau tại O.
Chứng minh rằng: 1/2.(AC+CB+BD+DA)<AB+CD<AC+CB+BD+DA