Thầy / cô giải giúp em bài này với ạ mai phải nộp mất rồi ạ :(

giúp em 7 bài này với ạ:(
sáng mai phải nộp bài rồi ạ
Bài 6:
Xét ΔOAC vuông tại A và ΔOBD vuông tại B có
OA=OB
\(\widehat{AOC}=\widehat{BOD}\)(hai góc đối đỉnh)
Do đó: ΔOAC=ΔOBD
=>OC=OD
Bài 7:
a: Ta có: \(\widehat{DAB}+\widehat{BAC}+\widehat{CAE}=180^0\)
=>\(\widehat{DAB}+\widehat{CAE}+90^0=180^0\)
=>\(\widehat{DAB}+\widehat{CAE}=90^0\)
mà \(\widehat{DAB}+\widehat{DBA}=90^0\)
nên \(\widehat{DBA}=\widehat{CAE}\)
Xét ΔABD vuông tại A và D và ΔCAE vuông tại E có
AB=AC
\(\widehat{DBA}=\widehat{EAC}\)
Do đó: ΔABD=ΔCAE
b: ta có: ΔABD=ΔCAE
=>DB=AE và AD=CE
DB+CE=DA+AE=DE
Dạ Em chào Thầy/Cô ạ!
Dạ Thầy/Cô giúp em giải bài này với ạ !
Em xin cảm ơn ạ

1: vecto AC=(-1;-7)
=>VTPT là (-7;1)
PTTS là:
x=3-t và y=6-7t
Phương trình AC là:
-7(x-3)+1(y-6)=0
=>-7x+21+y-6=0
=>-7x+y+15=0
2: Tọa độ M là:
x=(3+2)/2=2,5 và y=(6-1)/2=2,5
PTTQ đường trung trực của AC là:
-7(x-2,5)+1(y-2,5)=0
=>-7x+17,5+y-2,5=0
=>-7x+y+15=0
3: \(AB=\sqrt{\left(-1-3\right)^2+\left(3-6\right)^2}=5\)
Phương trình (A) là:
(x-3)^2+(y-6)^2=AB^2=25
Thầy Nguyễn Việt Lâm ơi giúp em mấy bài này với.Em sắp phải nộp rồi ạ 

4.
\(ab+bc+ca=3abc\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=3\)
Đặt \(\left(\dfrac{1}{a};\dfrac{1}{b};\dfrac{1}{c}\right)=\left(x;y;z\right)\Rightarrow x+y+z=3\)
\(S=\sum\dfrac{\dfrac{1}{y^2}}{\dfrac{1}{x}\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}\right)}=\sum\dfrac{x^3}{x^2+y^2}=\sum\left(x-\dfrac{xy^2}{x^2+y^2}\right)\)
\(S\ge\sum\left(x-\dfrac{xy^2}{2xy}\right)=\sum\left(x-\dfrac{y}{2}\right)=\dfrac{x+y+z}{2}=\dfrac{3}{2}\)
\(S_{min}=\dfrac{3}{2}\) khi \(x=y=z=1\) hay \(a=b=c=1\)
5.
Đặt \(\left(\dfrac{1}{a};\dfrac{2}{b};\dfrac{3}{c}\right)=\left(x;y;z\right)\Rightarrow x+y+z=3\)
Đặt vế trái là P
\(P=\dfrac{z^3}{x^2+z^2}+\dfrac{x^3}{x^2+y^2}+\dfrac{y^3}{y^2+z^2}\)
Quay lại dòng 3 của bài số 4
6.
Do a;b;c không âm, ta có:
\(b^2\left(b-1\right)^2\left(b+2\right)\ge0\)
\(\Leftrightarrow b^5-3b^3+2b^2\ge0\)
\(\Leftrightarrow b^5-3b^3+2b^2-6\ge-6\)
\(\Leftrightarrow-\left(3-b^2\right)\left(b^3+2\right)\ge-6\)
\(\Leftrightarrow6\ge\left(3-b^2\right)\left(b^3+2\right)\)
\(\Rightarrow\dfrac{1}{b^3+2}\ge\dfrac{3-b^2}{6}\)
\(\Rightarrow\dfrac{a}{b^3+2}\ge\dfrac{a\left(3-b^2\right)}{6}\)
Tương tự: \(\dfrac{b}{c^3+2}\ge\dfrac{b\left(3-c^2\right)}{6}\) ; \(\dfrac{c}{a^3+2}\ge\dfrac{c\left(3-a^2\right)}{6}\)
Cộng vế: \(P\ge\dfrac{a+b+c}{2}-\dfrac{ab^2+bc^2+ca^2+abc}{6}=\dfrac{3}{2}-\dfrac{ab^2+bc^2+ca^2+abc}{6}\)
Không mất tính tổng quát, giả sử \(b=mid\left\{a;b;c\right\}\)
\(\left(b-a\right)\left(b-c\right)\le0\)
\(\Leftrightarrow b^2+ac\le ab+bc\)
\(\Leftrightarrow ab^2+ca^2\le a^2b+abc\)
\(\Rightarrow ab^2+bc^2+ca^2+abc\le bc^2+a^2b+2abc=b\left(a+c\right)^2=4b\left(\dfrac{a+c}{2}\right)\left(\dfrac{a+c}{2}\right)\le\dfrac{4}{27}\left(a+b+c\right)^3=4\)
\(\Rightarrow P\ge\dfrac{3}{2}-\dfrac{4}{6}=\dfrac{5}{6}\)
Mọi người giúp em bài này vs ạ ! Em cần gấp lắm ạ , mai em phải nộp rồi ! Em cảm ơn ! 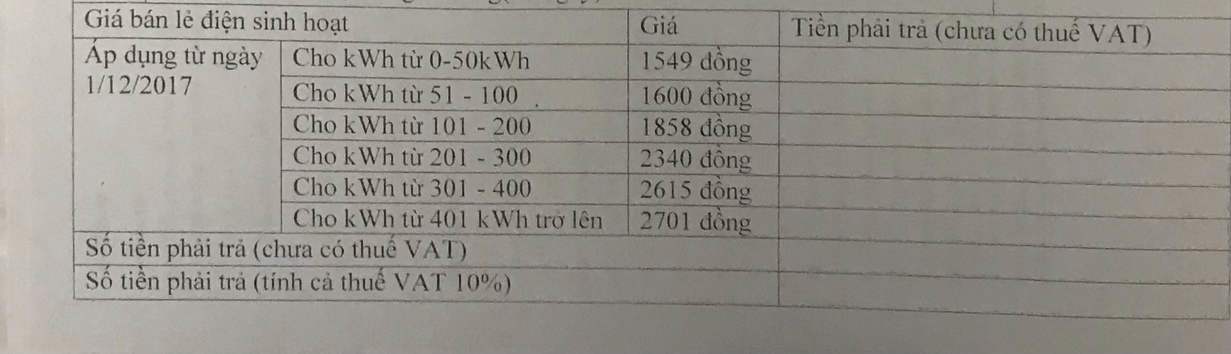
Giải gấp giúp mình 2 bài này với ạ, sáng mai mình nộp rồi. Giúp mình với ạ
Bài 5:
a: BC=10cm
b: HA=4,8cm
HB=3,6(cm)
HC=6,4(cm)
Bài 6:
\(x^3=6+3\sqrt[3]{\left(3+2\sqrt{2}\right)\left(3-2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\\ \Leftrightarrow x^3=6+3x\sqrt[3]{1}\\ \Leftrightarrow x^3-3x=6\\ y^3=34+3\sqrt[3]{\left(17+12\sqrt{2}\right)\left(17-12\sqrt{2}\right)}\left(\sqrt[3]{17+12\sqrt{2}}+\sqrt[3]{17-12\sqrt{2}}\right)\\ \Leftrightarrow y^3=34+3y\sqrt[3]{1}\\ \Leftrightarrow y^3-3y=34\\ \Leftrightarrow P=x^3-3x+y^3-3y+1980=6+34+1980=2020\)
gfrưerrrrrrrrrrr
cc giúp mk bài này với ạ,mai mk phải nộp rồi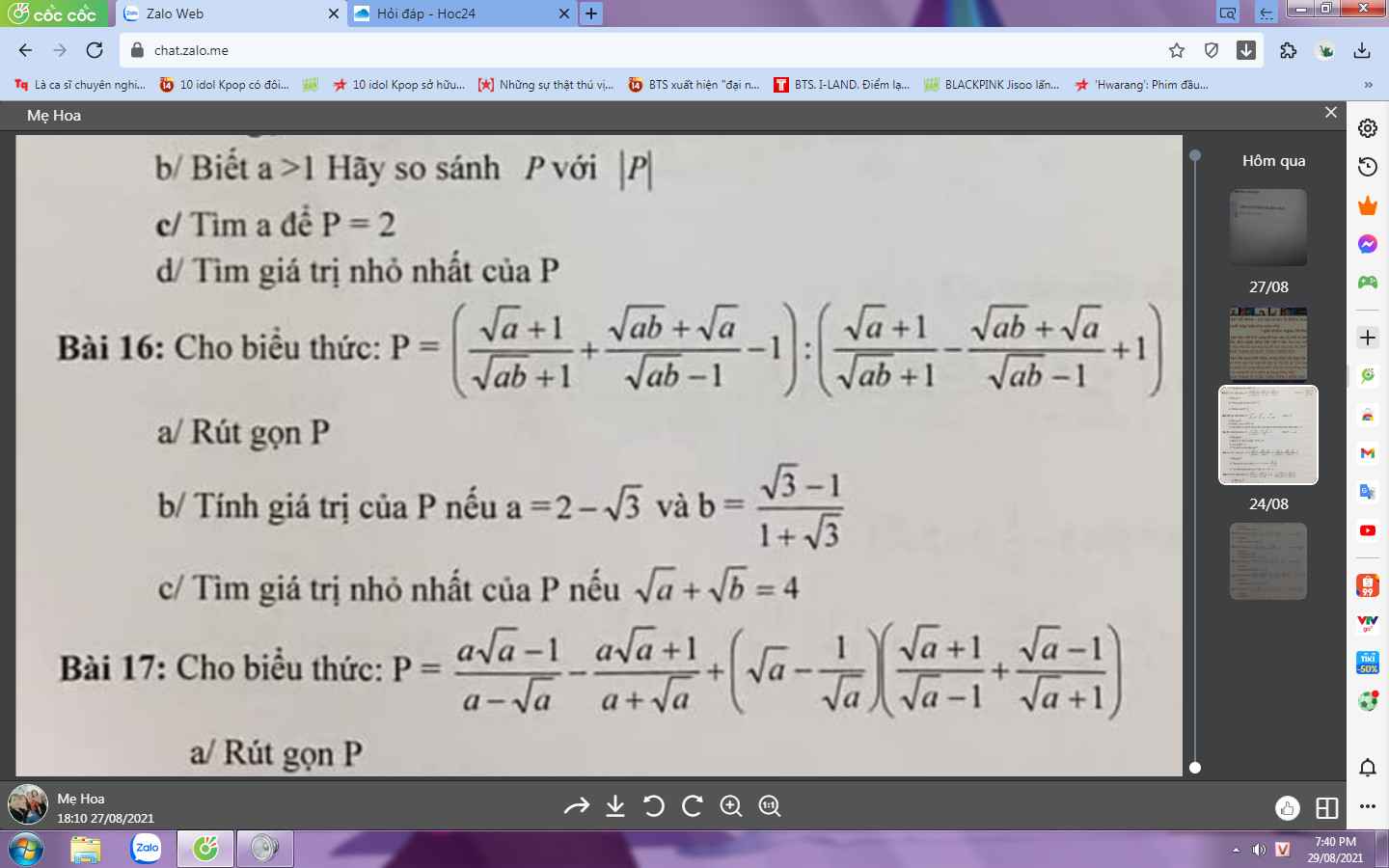
Bài 16:
a: Ta có: \(P=\left(\dfrac{\sqrt{a}+1}{\sqrt{ab}+1}+\dfrac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}-1\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{ab}+1}-\dfrac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}+1\right)\)
\(=\dfrac{a\sqrt{b}-\sqrt{a}+\sqrt{ab}-1+ab+\sqrt{ab}+a\sqrt{b}+\sqrt{a}-ab+1}{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}:\dfrac{a\sqrt{b}-\sqrt{a}+\sqrt{ab}-1-ab-\sqrt{ab}-a\sqrt{b}-\sqrt{a}+ab-1}{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}\)
\(=\dfrac{2a\sqrt{b}+2\sqrt{ab}}{-2\sqrt{a}-2}\)
\(=\dfrac{2\sqrt{ab}\left(\sqrt{a}+1\right)}{-2\left(\sqrt{a}+1\right)}\)
\(=-\sqrt{ab}\)
Tìm chữ số a và b để \(ababab4\) \(⋮\) \(72\)
Thầy cô giúp em với ạ cuối tuần em nộp bài rồi
Ta thấy tổng các chữ số của số \(\overline{ababab4}\) là \(a+b+a+b+a+b+4\)
\(=3a+3b+4\).
Do \(3a,3b⋮3\) và 4 không chia hết cho 3 nên \(3a+3b+4⋮̸3\). Điều này có nghĩa là số \(\overline{ababab4}\) không thể chia hết cho 3 dù a, b có là chữ số nào. Vì thế, không tồn tại chữ số a, b nào để \(\overline{ababab4}\) chia hết cho 72.
em hỏi xíu là vì sao lại xét dấu hiệu chia hết cho 3 ạ?
Ai có thể giải giúp tớ 2 bài này với ạ , Mai mình nộp rồi ạ
Bài văn văn này mai thứ 7 6/6 em phải nộp rồi mong mn giúp em ạ (Lưu ý kh chép mạng ạ )