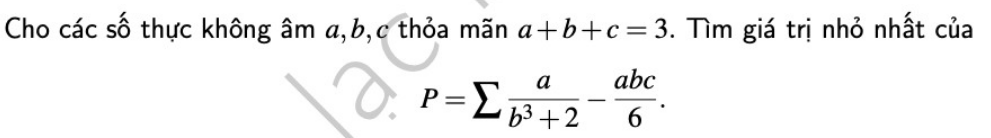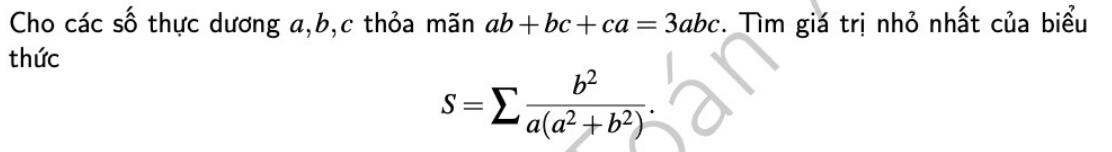4.
\(ab+bc+ca=3abc\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=3\)
Đặt \(\left(\dfrac{1}{a};\dfrac{1}{b};\dfrac{1}{c}\right)=\left(x;y;z\right)\Rightarrow x+y+z=3\)
\(S=\sum\dfrac{\dfrac{1}{y^2}}{\dfrac{1}{x}\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}\right)}=\sum\dfrac{x^3}{x^2+y^2}=\sum\left(x-\dfrac{xy^2}{x^2+y^2}\right)\)
\(S\ge\sum\left(x-\dfrac{xy^2}{2xy}\right)=\sum\left(x-\dfrac{y}{2}\right)=\dfrac{x+y+z}{2}=\dfrac{3}{2}\)
\(S_{min}=\dfrac{3}{2}\) khi \(x=y=z=1\) hay \(a=b=c=1\)
5.
Đặt \(\left(\dfrac{1}{a};\dfrac{2}{b};\dfrac{3}{c}\right)=\left(x;y;z\right)\Rightarrow x+y+z=3\)
Đặt vế trái là P
\(P=\dfrac{z^3}{x^2+z^2}+\dfrac{x^3}{x^2+y^2}+\dfrac{y^3}{y^2+z^2}\)
Quay lại dòng 3 của bài số 4
6.
Do a;b;c không âm, ta có:
\(b^2\left(b-1\right)^2\left(b+2\right)\ge0\)
\(\Leftrightarrow b^5-3b^3+2b^2\ge0\)
\(\Leftrightarrow b^5-3b^3+2b^2-6\ge-6\)
\(\Leftrightarrow-\left(3-b^2\right)\left(b^3+2\right)\ge-6\)
\(\Leftrightarrow6\ge\left(3-b^2\right)\left(b^3+2\right)\)
\(\Rightarrow\dfrac{1}{b^3+2}\ge\dfrac{3-b^2}{6}\)
\(\Rightarrow\dfrac{a}{b^3+2}\ge\dfrac{a\left(3-b^2\right)}{6}\)
Tương tự: \(\dfrac{b}{c^3+2}\ge\dfrac{b\left(3-c^2\right)}{6}\) ; \(\dfrac{c}{a^3+2}\ge\dfrac{c\left(3-a^2\right)}{6}\)
Cộng vế: \(P\ge\dfrac{a+b+c}{2}-\dfrac{ab^2+bc^2+ca^2+abc}{6}=\dfrac{3}{2}-\dfrac{ab^2+bc^2+ca^2+abc}{6}\)
Không mất tính tổng quát, giả sử \(b=mid\left\{a;b;c\right\}\)
\(\left(b-a\right)\left(b-c\right)\le0\)
\(\Leftrightarrow b^2+ac\le ab+bc\)
\(\Leftrightarrow ab^2+ca^2\le a^2b+abc\)
\(\Rightarrow ab^2+bc^2+ca^2+abc\le bc^2+a^2b+2abc=b\left(a+c\right)^2=4b\left(\dfrac{a+c}{2}\right)\left(\dfrac{a+c}{2}\right)\le\dfrac{4}{27}\left(a+b+c\right)^3=4\)
\(\Rightarrow P\ge\dfrac{3}{2}-\dfrac{4}{6}=\dfrac{5}{6}\)