Giải phương trình : sin^2x - 3sinxcosx = -1
PC
Những câu hỏi liên quan
CỨU MÌNH VS
a) 3Cos^2x -2Sin2x + Sin^2x =1
b) 4Cos^2x -3SinxCosx +3Sin^2x =1
a/
\(\Leftrightarrow3cos^2x-4sinx.cosx+1-cos^2x=1\)
\(\Leftrightarrow2cos^2x-4sinx.cosx=0\)
\(\Leftrightarrow2cosx\left(cosx-2sinx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\tanx=\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\x=arctan\left(\frac{1}{2}\right)+k\pi\end{matrix}\right.\)
b.
Nhận thấy \(cosx=0\) ko phải nghiệm, chia 2 vế cho \(cos^2x\)
\(4-3tanx+3tan^2x=1+tan^2x\)
\(\Leftrightarrow2tan^2x-3tanx+3=0\)
Pt vô nghiệm
\(sin^2x+sin^22x=1\)
Giải giúp mình phương trình này với ???
\(sin^2x+sin^22x=1\)
\(\Leftrightarrow2sin^2x-1+2sin^22x-2=-1\)
\(\Leftrightarrow-cos2x-2cos^22x+1=0\)
\(\Leftrightarrow\left(cos2x+1\right)\left(2cos2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=-1\\cos2x=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\pi+k2\pi\\2x=\pm\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\pm\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Giải phương trình: Cos^2x - sin2x - sin^2x = 1.
Xem chi tiết
\(cos^2x-sin2x-sin^2x=1\)
\(\Leftrightarrow1-sin^2x-2sinx.cosx-sin^2x=1\)
\(\Leftrightarrow sin^2x+sinx.cosx=0\)
\(\Leftrightarrow sinx\left(sinx+cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\tanx=-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=-\dfrac{\pi}{4}+k\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Giải phương trình
\(\left(sin^2x+\dfrac{1}{sin^2x}\right)+4\left(sinx+\dfrac{1}{sinx}\right)-7=0\)
Giải phương trình:
a, \(2sin^2x+2sinxcosx-3cos^2x=0\).
b, \(2sin^2x-3sinxcosx+cos^2x=0\).
c, \(2sin^2x-5sinxcosx+3cos^2x=0\).
b) \(2sin^2x-3sinxcosx+cos^2x=0\)
\(\Leftrightarrow2tan^2x-3tanx+1=0\left(cosx\ne0\Leftrightarrow x\ne\dfrac{\pi}{2}+k\pi\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=1\\tanx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=tan\dfrac{\pi}{4}\\tanx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=arctan\left(\dfrac{1}{2}\right)+k\pi\end{matrix}\right.\left(k\in Z\right)\)
Đúng 2
Bình luận (0)
(Sin22x-2) / (Sin22x-4Cos2x) = Tan2x4Cos2x + 3SinxCosx - Sin2x = 32Sin2x - SinxCosx - Cos2x = 2
Xem chi tiết
Giải chi tiết giùm mình nhé
Giải phương trình lượng giác:
1.sin^2x + sin 2x = 3 cos^2x
2.sinx + cosx = 2√2 sinxcosx
1. \(\sin^2x+\sin2x=3\cos^2x\Leftrightarrow\sin^2x+2\sin x\cos x-3\cos^2x=0\Leftrightarrow4\sin^2x+2\sin x\cos x-3=0\)
Vì \(\cos x=0\) không phải là nghiệm của phương trình, nên chia 2 vế pt cho \(\cos x\), ta đc:
\(4\tan^2x+2\tan x-\frac{3}{\cos^2x}=0\Leftrightarrow4\tan^2x+2\tan x-3\left(1+\tan^2x\right)=0\Leftrightarrow\tan^2x+2\tan x-3=0\)
Suy ra: \(\begin{matrix}\tan x=1\\\tan x=-3\end{matrix}\) suy ra x.
Đúng 1
Bình luận (0)
b) \(\Leftrightarrow\sqrt{2}\sin\left(x+\frac{\pi}{4}\right)=\sqrt{2}\sin2x\Leftrightarrow\sin\left(x+\frac{\pi}{4}\right)=\sin2x\Leftrightarrow\begin{cases}x+\frac{\pi}{4}=2x+k2\pi\\x+\frac{\pi}{4}=\pi-2x+k2\pi\end{cases}\)
\(\Leftrightarrow\begin{cases}x=\frac{\pi}{4}-k2\pi\\x=\frac{\pi}{4}+\frac{k2\pi}{3}\end{cases}\)
Vậy ....
Đúng 0
Bình luận (0)
Chỗ Viết các nghiệm: Sửa lại : dùng dấu ngoặc vuông thay cho ngoặc nhọn
Đúng 0
Bình luận (0)
Giải phương trình sau:
a, \(\sin\left(2x\right)+\sin\left(x\right)-\dfrac{1}{2\sin\left(x\right)}-\dfrac{1}{\sin\left(2x\right)}=2\cot\left(2x\right)\)
b, \(\left(\sin\left(2x\right)+cos\left(2x\right)\right)cos\left(x\right)+2cos\left(2x\right)-sin\left(x\right)=0\)
c, \(\sin\left(2x\right)-\cos\left(2x\right)+3\sin\left(x\right)-\cos\left(x\right)-1=0\)
b)
(sin2x + cos2x)cosx + 2cos2x - sinx = 0
⇔ cos2x (cosx + 2) + sinx (2cos2 x – 1) = 0
⇔ cos2x (cosx + 2) + sinx.cos2x = 0
⇔ cos2x (cosx + sinx + 2) = 0
⇔ cos2x = 0
⇔ 2x = 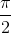 + kπ ⇔ x =
+ kπ ⇔ x = 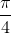 + k
+ k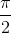 (k ∈
(k ∈ 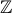 )
)
Đúng 0
Bình luận (0)
c)
Đáp án:
x=π6π6+ k2ππ
và x= 5π65π6+k2ππ (k∈Z)
Lời giải:
sin2x-cos2x+3sinx-cosx-1=0
⇔ 2sinxcosx-(1-2sin²x) +3sinx-cosx-1=0
⇔ 2sin²x+2sinxcosx+3sinx-cosx-2=0
⇔ (2sin²x+3sinx-2)+ cosx(2sinx-1)=0
⇔ (2sinx-1)(sinx+2)+cosx(2sinx-1)=0
⇔ (2sinx-1)(sinx+cosx+2)=0
⇔ sinx=1212
⇔ x=π6π6+ k2ππ
hoặc x= 5π65π6+k2ππ (k∈Z)
(sinx+cosx+2)=0 (vô nghiệm do sinx+cosx+2=√22sin(x+π4π4)+2>0)
Đúng 0
Bình luận (0)
Giải phương trình
\(\left(3-4\sin^2x\right)\left(3-4\sin^23x\right)=1-2\cos10x\)
Với \(sinx=0\) không phải nghiệm (vế trái bằng 9, vế phải hiển nhiên nhỏ hơn 9)
Với \(sinx\ne0\):
\(\Rightarrow\left(3sinx-4sin^3x\right)\left(3-4sin^23x\right)=sinx-2sinx.cos10x\)
\(\Leftrightarrow sin3x\left(3-4sin^23x\right)=sinx-2sinx.cos10x\)
\(\Leftrightarrow3sin3x-4sin^33x=sinx-sin11x+sin9x\)
\(\Leftrightarrow sin9x=sinx-sin11x+sin9x\)
\(\Leftrightarrow sin11x=sinx\)
\(\Leftrightarrow...\)
Đúng 1
Bình luận (0)




