Chứng minh các bất đẳng thức sau:
a) tanx > x (0 < x < ); b) tanx > x +
(0 < x <
).
Chứng minh các bất đẳng thức sau: tan x > x 0 < x < π 2
Xét hàm số y = f(x) = tanx – x trên khoảng (0; π/2)
Ta có: y’ = 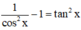 > 0 với ∀ x ∈ R.
> 0 với ∀ x ∈ R.
⇒ hàm số đồng biến trên khoảng (0; π/2)
⇒ f(x) > f(0) = 0 với ∀ x > 0
hay tan x – x > 0 với ∀ x ∈ (0; π/2)
⇔ tan x > x với ∀ x ∈ (0; π/2) (đpcm).
Chứng minh các bất đẳng thức sau: tan x > x + x 3 3 0 < x < π 2
Xét hàm số y = g(x) = tanx - x - 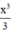 trên
trên 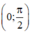
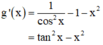
Theo kết quả câu a): tanx > x ∀ x ∈ 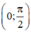
⇒ g'(x) > 0 ∀ x ∈ 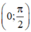
⇒ y = g'(x) đồng biến trên 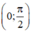
⇒ g(x) > g(0) = 0 với ∀ x ∈ 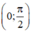
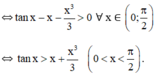
Chứng minh các bất đẳng thức sau: tanx > sinx, 0 < x < π /2
Xét hàm số f(x) = tanx − sinx trên nửa khoảng [0; π /2);

x ∈ [0;1/2)
Dấu “=” xảy ra khi x = 0.
Suy ra f(x) đồng biến trên nửa khoảng [0; π /2)
Mặt khác, ta có f(0) = 0, nên f(x) = tanx – sinx > 0 hay tanx > sinx với mọi x ∈ [0; 1/2)
Chứng minh các bất đẳng thức sau:
a) tanx > sinx, 0 < x < π/2
b) 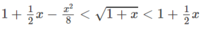
với 0 < x < + ∞
a) Xét hàm số f(x) = tanx − sinx trên nửa khoảng [0; π/2);

x ∈ [0;1/2)
Dấu “=” xảy ra khi x = 0.
Suy ra f(x) đồng biến trên nửa khoảng [0; π/2)
Mặt khác, ta có f(0) = 0, nên f(x) = tanx – sinx > 0 hay tanx > sinx với mọi x ∈ [0; 1/2)
b) Xét hàm số h(x) trên [0; + ∞ )
![]()
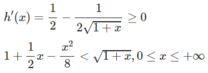
Dấu “=” xẩy ra chỉ tại x = 0 nên h(x) đồng biến trên nửa khoảng [0; + ∞ ).
Vì h(x) = 0 nên
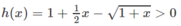
Hay
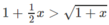
Xét hàm số trên f(x) trên [0; + ∞ );
![]()
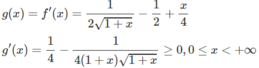
Vì g(0) = 0 và g(x) đồng biến trên nửa khoảng [0; + ∞ ) nên g(x) ≥ 0, tức là f′(x) ≥ 0 trên khoảng đó và vì dấu “=” xảy ra chỉ tại x = 0 nên f(x) đồng biến trên nửa khoảng .
Mặt khác, ta có f(0) = 0 nên
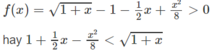
Với mọi 0 < x < + ∞ .
Chứng minh các bất đẳng thức sau:
a) \(tanx > x (0 < x < \dfrac{\pi}{2})\)
b) \(tanx > x + \dfrac{x^3}{3} (0 < x < \dfrac{\pi}{2})\)
a) Xét hàm số y = f(x) = tanx – x với x ∈ [0 ; ).
Ta có : y’ = - 1 ≥ 0, x ∈ [0 ;
); y’ = 0 ⇔ x = 0. Vậy hàm số luôn đồng biến trên [0 ;
).
Từ đó ∀x ∈ (0 ; ) thì f(x) > f(0) ⇔ tanx – x > tan0 – 0 = 0 hay tanx > x.
b) Xét hàm số y = g(x) = tanx – x - . với x ∈ [0 ;
).
Ta có : y’ = - 1 - x2 = 1 + tan2x - 1 - x2 = tan2x - x2
= (tanx - x)(tanx + x), ∀x ∈ [0 ; ).
Vì ∀x ∈ [0 ; ) nên tanx + x ≥ 0 và tanx - x >0 (theo câu a).
Do đó y' ≥ 0, ∀x ∈ [0 ; ).
Dễ thấy y' = 0 ⇔ x = 0. Vậy hàm số luôn đồng biến trên [0 ; ). Từ đó : ∀x ∈ [0 ;
) thì g(x) > g(0) ⇔ tanx – x -
> tan0 - 0 - 0 = 0 hay tanx > x +
.
Chứng minh các bất đẳng thức sau với x, y, z > 0
Chứng minh các bất đẳng thức sau:
1 + 1 2 x - x 2 8 < 1 + x < 1 + 1 2 x
với 0 < x < + ∞
Xét hàm số h(x) trên [0; + ∞ )
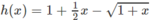
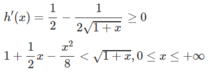
Dấu “=” xẩy ra chỉ tại x = 0 nên h(x) đồng biến trên nửa khoảng [0; + ∞ ).
Vì h(x) = 0 nên
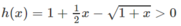
Hay
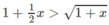
Xét hàm số trên f(x) trên [0; + ∞ );
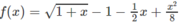
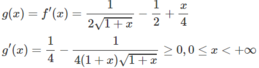
Vì g(0) = 0 và g(x) đồng biến trên nửa khoảng [0; + ∞ ) nên g(x) ≥ 0, tức là f′(x) ≥ 0 trên khoảng đó và vì dấu “=” xảy ra chỉ tại x = 0 nên f(x) đồng biến trên nửa khoảng .
Mặt khác, ta có f(0) = 0 nên
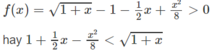
Với mọi 0 < x < + ∞
Chứng minh các bất đẳng thức sau: \(\dfrac{x}{y}+\dfrac{y}{x}\ge2\left(\forall x,y>0\right)\)
Biến đổi tương đương:
\(\Leftrightarrow\dfrac{x^2+y^2}{xy}\ge2\)
\(\Leftrightarrow x^2+y^2\ge2xy\)
\(\Leftrightarrow x^2+y^2-2xy\ge0\)
\(\Leftrightarrow\left(x-y\right)^2\ge0\) (luôn đúng)
Vậy BĐT đã được chứng minh
Cách khác so với anh Nguyễn Việt Lâm
Ta có: \(\dfrac{x}{y}+\dfrac{y}{x}\ge2\sqrt{\dfrac{x}{y}\cdot\dfrac{y}{x}}=2\) (đpcm)
Cho góc bất kì α. Chứng minh các đẳng thức sau:
a) (sinα+cosα)2=1+sin2α;
b) cos4α−sin4α=cos2α.
a: (sina+cosa)^2
=sin^2a+cos^2a+2*sina*cosa
=1+sin2a
b: \(cos^4a-sin^4a=\left(cos^2a-sin^2a\right)\left(cos^2a+sin^2a\right)\)
\(=cos^2a-sin^2a=cos2a\)
Chứng minh đẳng thức, bất đẳng thức: \(x^2+x+1>0\) với mọi x
Lời giải:
$x^2+x+1=x^2+2.x.\frac{1}{2}+(\frac{1}{2})^2+\frac{3}{4}$
$=(x+\frac{1}{2})^2+\frac{3}{4}$
$\geq 0+\frac{3}{4}$
$> 0$
Ta có đpcm.