Cho biểu thức A =( x+1/x-1 - x-1/x+1 + x2 -4x-1/x2 -1) . x+2003/x Rút gọn biểu thức
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
HT
Những câu hỏi liên quan
cho biểu thức A=x-3/x2-x+1-1/x+1+4x+4/x3+1 a, rút gọn biểu thứcA
\(A=\dfrac{x^2-2x-3-x^2+x-1+4x+4}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{3x}{\left(x+1\right)\left(x^2+x+1\right)}\)
Đúng 1
Bình luận (0)
Bài 2. Rút gọn các biểu thức sau : A (x - 3)(x + 7) – (x + 5)(x - 1) B - 2(2x + 5)2 – (4x + 1)(1 – 4x) C x2(x – 4)(x + 4) – (x2 + 1)(x2 - 1) D (x + 1)(x2 – x + 1) – (x – 1)(x2 + x +1)E (x – 1)3 – (x – 1)(x2 + x + 1) – (3x + 1)(1 – 3x)
Đọc tiếp
Bài 2. Rút gọn các biểu thức sau :
A = (x - 3)(x + 7) – (x + 5)(x - 1) B = - 2(2x + 5)2 – (4x + 1)(1 – 4x)
C = x2(x – 4)(x + 4) – (x2 + 1)(x2 - 1) D = (x + 1)(x2 – x + 1) – (x – 1)(x2 + x +1)
E = (x – 1)3 – (x – 1)(x2 + x + 1) – (3x + 1)(1 – 3x)
\(A=x^2+4x-21-x^2-4x+5=-16\\ B=-2\left(4x^2+20x+25\right)-\left(1-16x^2\right)\\ B=-8x^2-40x-50-1+16x^2=8x^2-40x-51\\ C=x^2\left(x^2-16\right)-\left(x^4-1\right)=x^4-16x^2-x^4+1=1-16x^2\\ D=x^3+1-\left(x^3-1\right)=2\\ E=x^3-3x^2+3x-1-x^3+1-9x^2+1=-12x^2+3x+1\)
Đúng 0
Bình luận (0)
Cho biểu thức sau:
A=(1/x-1 - x/1-x^2 . x2 + x + 1/x+ 1) : 2x +1/ x2 +2x+1
a) Rút gọn biểu thức A
b) Tính giá trị của A khi x= 1/2
Cho biểu thức A left(dfrac{4x}{x+2}+dfrac{8x^2}{4-x^2}right):left(dfrac{x-1}{x^2-2x}-dfrac{2}{x}right)(x+24x+4−x28x2):(x2−2xx−1−x2)
a) Tìm x để giá trị của biểu thức biểu thức A được xác định.
b) Rút gọn A.
c) Tìm giá trị của A biết x2 + 2x 15
d) Tìm x biết |A| A
Đọc tiếp
Cho biểu thức A =
a) Tìm x để giá trị của biểu thức biểu thức A được xác định.
b) Rút gọn A.
c) Tìm giá trị của A biết x2 + 2x = 15
d) Tìm x biết |A| > A
Cho biểu thức P 1+ 3/x2+5x+6 : ( 8x2/ 4x3-8x2 - 3x/ 3x2-12 -1/x+2)A) Rút gọn PB) Tìm các giá trị của x để P 0; P 1C) Tìm cã giá trị của x để P 0Cho biểu thứcQ (2x-x2/ 2x2 +8 - 2x2/ 3x3-2x2+4x-8) (2/x2 + 1-x/x)A) Rút gọn QB) Tìm giá trị nguyên của x để Q có giá trị nguyên
Đọc tiếp
Cho biểu thức P= 1+ 3/x2+5x+6 : ( 8x2/ 4x3-8x2 - 3x/ 3x2-12 -1/x+2)
A) Rút gọn P
B) Tìm các giá trị của x để P= 0; P= 1
C) Tìm cã giá trị của x để P> 0
Cho biểu thức
Q= (2x-x2/ 2x2 +8 - 2x2/ 3x3-2x2+4x-8) (2/x2 + 1-x/x)
A) Rút gọn Q
B) Tìm giá trị nguyên của x để Q có giá trị nguyên
Bài 1:
a) Ta có: \(P=1+\dfrac{3}{x^2+5x+6}:\left(\dfrac{8x^2}{4x^3-8x^2}-\dfrac{3x}{3x^2-12}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\left(\dfrac{8x^2}{4x^2\left(x-2\right)}-\dfrac{3x}{3\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\left(\dfrac{4}{x-2}-\dfrac{x}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\dfrac{4\left(x+2\right)-x-\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}\cdot\dfrac{\left(x-2\right)\left(x+2\right)}{4x+8-x-x+2}\)
\(=1+3\cdot\dfrac{\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=1+\dfrac{3\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{\left(x+3\right)\left(2x+10\right)+3\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{2x^2+10x+6x+30+3x-6}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{2x^2+19x-6}{\left(x+3\right)\left(2x+10\right)}\)
Đúng 0
Bình luận (0)
Cho biểu thức :
P
x
2
-
2
x
2
x
2
+
8
-
2
x
2
8...
Đọc tiếp
Cho biểu thức : P = x 2 - 2 x 2 x 2 + 8 - 2 x 2 8 - 4 x + 2 x 2 - x 3 1 - 1 x - 2 x 2 x ≠ 0 , x ≠ 2
a) Rút gọn biểu thức P
b) Tính giá trị biểu thức P với x = 1/2
a) Ta có: 2x2 + 8 = 2(x2 + 4).
8 – 4x + 2x2 – x3
= (8 – x3) - ( 4x - 2x2)
= (2 – x).(4 + 2x + x2) - 2x.(2 - x)
= (2 – x).(4 + 2x + x2 – 2x)
= (2 - x). (4 + x2 )
* Do đó:
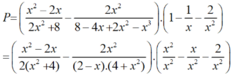
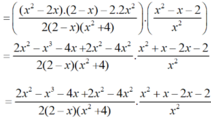
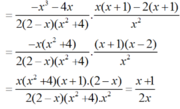
b) Tại x = 1 2 hàm số đã cho xác định nên thay x = 1 2 vào biểu thức rút gọn của P ta được:
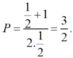
Đúng 0
Bình luận (0)
.Cho biểu thức A ( x - 5 ) ( x2 + 5x + 25) - ( x – 2)(x+ 2) + x.(x2 + x + 4)
a) Rút gọn biểu thức A
b) Tính giá trị biểu thức A biết x -2
b) Tính giá trị biểu thức A biết x2 – 1 0
Đọc tiếp
.Cho biểu thức A = ( x - 5 ) ( x2 + 5x + 25) - ( x – 2)(x+ 2) + x.(x2 + x + 4)
a) Rút gọn biểu thức A
b) Tính giá trị biểu thức A biết x = -2
b) Tính giá trị biểu thức A biết x2 – 1 = 0
a) A = (x - 5)(x² + 5x + 25) - (x - 2)(x + 2) + x(x² + x + 4)
= x³ - 125 - x² + 4 + x³ + x² + 4x
= (x³ + x³) + (-x² + x²) + 4x + (-125 + 4)
= 2x³ + 4x - 121
b) Tại x = -2 ta có:
A = 2.(-2)³ + 4.(-2) - 121
= 2.(-8) - 8 - 121
= -16 - 129
= -145
c) x² - 1 = 0
x² = 1
x = -1; x = 1
*) Tại x = -1 ta có:
A = 2.(-1)³ + 4.(-1) - 121
= 2.(-1) - 4 - 121
= -2 - 125
= -127
*) Tại x = 1 ta có:
A = 2.1³ + 4.1 - 121
= 2.1 + 4 - 121
= 2 - 117
= -115
Đúng 0
Bình luận (0)
a) rút gọn biểu thức sau :(x+2)(x-2)-(x-3)(x+1)
b)Tìm x biết : x2-4x+3=0
a)=\(x^2-4-x^2+2x+3=2x-1\)
b)\(x^2-4x+3=0\)
\(\Leftrightarrow x^2-x-3x+3=0\)
\(\Leftrightarrow x\left(x-1\right)-3\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\x-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho biểu thức : A= x-1/3x và B= ( x+1/2x-2 + 3x-1/x2 - 1 - x+3/2x+2) : 3/x+1 Với x # 0,x# -1,1.
a)Rút gọn biểu thức B
b)Tính giá trị của biểu thức A khi x thỏa mãn x2 - 2x = 0
c) tìm giá trị của x để B/A đạt giá trị nhỏ nhất .
b: \(A=\dfrac{2-1}{3\cdot2}=\dfrac{1}{6}\)
Đúng 0
Bình luận (0)




