Phân tích hằng số sau và chứng minh không phụ thuộc vào x
B= 4(sin4x+cos4x) - cos4x
Chứng minh biểu thức sau đây không phụ thuộc vào x
A = 3(sin4x + cos4x) -2(sin6x+cos6x)
\(A=3\left[\left(sin^2x+cos^2x\right)^2-2\cdot sin^2x\cdot cos^2x\right]-2\left[\left(sin^2x+cos^2x\right)^3-3\cdot sin^2x\cdot cos^2x\left(sin^2x+cos^2x\right)\right]\)
\(=3\left[1-2\cdot sin^2x\cdot cos^2x\right]-2\left[1-3\cdot sin^2x\cdot cos^2x\right]\)
\(=3-6\cdot sin^2x\cdot cos^2x-2+6\cdot sin^2x\cdot cos^2x\)
=1
Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào x.
A = 2( sin 4 x + cos 4 x + sin 2 x . cos 2 x ) 2 - ( sin 8 x + cos 8 x )
Ta có:
![]()
![]()
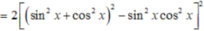

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Vậy giá trị của biểu thức  không phụ thuộc vào x.
không phụ thuộc vào x.
Câu 1 : Chứng minh rằng : 3 - 4sin2x = 4cos2x - 1Câu 2 : Chứng minh rằng : cos4x - sin4x = 2cos2x - 1 = 1 - 2sin2xCâu 3 : Chứng minh rằng : sin4x + cos4x = 1 - 2sin2xCos2x
1/ \(3-4\sin^2=4\cos^2x-1\Leftrightarrow4\left(\sin^2x+\cos^2x\right)-4=0\Leftrightarrow4.1-4=0\left(ld\right)\Rightarrow dpcm\)
2/ \(\cos^4x-\sin^4x=\left(\cos^2x+\sin^2x\right)\left(\cos^2x-\sin^2x\right)=\cos^2x-\left(1-\cos^2x\right)=2\cos^2x-1=\left(1-\sin^2x\right)-\sin^2x=1-2\sin^2x\)
3/ \(\sin^4x+\cos^4x=\left(\sin^2x+\cos^2x\right)^2-2\sin^2x.\cos^2x=1-2\sin^2x.\cos^2x\)
Chứng minh các đẳng thức sau (giả sử các biểu thức sau đều có nghĩa)
a) sin4x + cos4x = 1 – 2sin2cos2x
b)
c)
a) \(sin^4x+cos^4x=\left(sin^2x\right)^2+\left(cos^2x\right)^2\)
\(=\left(sin^2x\right)^2+2sin^2xcos^2x+\left(cos^2x\right)^2-2sin^2xcos^2x\)
\(=\left(sin^2x+cos^2x\right)^2-2sin^2xcos^2x\)
\(=1-2sin^2xcos^2x\)
b) \(\dfrac{1+cotx}{1-cotx}=\dfrac{tanx.cotx+cotx}{tanx.cotx-cotx}\)
\(=\dfrac{cotx.\left(tanx+1\right)}{cotx.\left(tanx-1\right)}\)
\(=\dfrac{tanx+1}{tanx-1}\)
c) \(\dfrac{cosx+sinx}{cos^3x}=\dfrac{1}{cos^2x}+\dfrac{tanx}{cos^2x}\)
\(=1+tan^2x+tanx.\dfrac{1}{cos^2x}\)
\(=1+tan^2x+tanx.\left(1+tan^2x\right)\)
\(=1+tan^2x+tanx+tan^3x\)
\(=tan^3x+tan^2x+tanx+1\)
Chứng minh các đẳng thức sau (giả sử các biểu thức sau đều có nghĩa)
a) sin4x + cos4x = 1 – 2sin2cos2x
b)
c)
Lời giải:
a.
$\sin ^4x+\cos ^4x=(\sin ^2x+\cos ^2x)^2-2\sin ^2x\cos ^2x$
$=1-2\sin ^2x\cos ^2x$
b.
$\frac{1+\cot x}{1-\cot x}=\frac{1+\frac{\cos x}{\sin x}}{1-\frac{\cos x}{\sin x}}=\frac{\cos x+\sin x}{\sin x-\cos x}(1)$
$\frac{\tan x+1}{\tan x-1}=\frac{\frac{\sin x}{\cos x}+1}{\frac{\sin x}{\cos x}-1}=\frac{\cos x+\sin x}{\sin x-\cos x}(2)$
Từ $(1); (2)$ ta có đpcm
c.
$\frac{\cos x+\sin x}{\cos ^3x}=(1+\frac{\sin x}{\cos x}).\frac{1}{\cos ^2x}$
$=(1+\tan x).\frac{\sin ^2x+\cos ^2x}{\cos ^2x}$
$=(1+\tan x)(\tan ^2x+1)=\tan ^3x+\tan ^2x+\tan x+1$
Ta có đpcm.
CHỨNG MINH ĐẲNG THỨC
a/ Chứng minh rằng: \(\frac{sin4x-sin2x}{1-cos2x+cos4x}=tanx\)( với x là giá trị để biểu thức có nghĩa)
b/ Cho x ≠ k\(\frac{\pi}{4}\) , kϵ Z . Chứng minh đẳng thức sau:\(\frac{1-cos4x}{sin4x}=tanx\)
\(\frac{sin4x-sin2x}{1-cos2x+cos4x}=\frac{2sin2x.cos2x-sin2x}{1-cos2x+2cos^22x-1}=\frac{sin2x\left(2cos2x-1\right)}{cos2x\left(2cos2x-1\right)}=\frac{sin2x}{cos2x}=tan2x\)
\(\Rightarrow\) đề sai
b/
\(\frac{1-cos4x}{sin4x}=\frac{1-\left(1-2sin^22x\right)}{2sin2x.cos2x}=\frac{2sin^22x}{2sin2x.cos2x}=\frac{sin2x}{cos2x}=tan2x\)
Đề sai tiếp lần 2
Cho 0 <x< 90 0 . Chứng minh các đẳng thức sau:
a, sin 4 x + cos 4 x = 1 - 2 sin 2 x cos 2 x
b, sin 6 x + cos 6 x = 1 - 3 sin 2 x cos 2 x
a, Ta có: sin 4 x + cos 4 x = sin 2 x + cos 2 x 2 - 2 sin 2 x . cos 2 x = 1 - 2 sin 2 x . cos 2 x
b, Ta có: sin 6 x + cos 6 x = sin 2 x + cos 2 x 3 - 3 sin 2 x cos 2 x sin 2 x + cos 2 x = 1 - 3 sin 2 x cos 2 x
Chứng minh các đẳng thức sau:
(với x là giá trị để biểu thức có nghĩa)
1/ \(\frac{\sin2x-\sin4x}{1-\cos2x+\cos4x}=-\tan2x\)
2/ \(\frac{\sin4x-\sin2x}{1-\cos2x+\cos4x}=\tan2x\)
\(\frac{sin2x-sin4x}{1-cos2x+cos4x}=\frac{sin2x-2sin2x.cos2x}{1-cos2x+2cos^22x-1}=\frac{sin2x\left(1-2cos2x\right)}{-cos2x\left(1-2cos2x\right)}=\frac{-sin2x}{cos2x}=-tan2x\)
\(\frac{sin4x-sin2x}{1-cos2x+cos4x}=-\left(\frac{sin2x-sin4x}{1-cos2x+cos4x}\right)=-\left(-tan2x\right)=tan2x\) lấy luôn kết quả câu trên cho lẹ, biến đổi thì làm y hệt
Tìm tất cả các giá trị của m để phương trình sin 4 x + cos 4 x + cos 2 4 x = m có 4 nghiệm phân biệt thuộc đoạn - π 4 ; π 4 .
A. m ≤ 47 64 hoặc m ≥ 3 2
B. 47 64 < m < 3 2
C. 47 64 < m ≤ 3 2
D. 47 64 ≤ m ≤ 3 2