Cho \(S_n=\sqrt{x^2-2nx+n^2}\)
Tìm GTNN của \(f\left(x\right)=S_1+S_2+S_3\)
Cho \(S_n=\frac{1}{n^2\left(n+2\right)\sqrt{n+1}}\)Chứng minh rằng: \(S_1+S_2+...+S_n< \frac{1}{2\sqrt{2}}\)
cho \(S_n=\frac{\sqrt{3}+S_{n-1}}{1-\sqrt{3}S_{n-1}}\) với n ϵ N và n ≥ 2, biết \(S_n=1\)
Tính \(S=S_1+S_2+S_3+...+S_{2005}\)
\(S_1=1\) (còn \(S_n=1\Rightarrow S=2015\))
Tính được \(S_1=1;S_2=-2-\sqrt{3};S_3=-2+\sqrt{3};S_4=1\)
Vậy \(S_i=S_{i+3}\left(i\ge1\right)\)
Mà \(S_1+S_2+S_3=-3\)
\(\Rightarrow S=\sum\limits^{2015}_{i=1}\left(S_i\right)=-3\cdot668+S_{2015}=-3\cdot668+1=-2003\)
#Kaito#
Cho \(S_n=\frac{2}{\left(2n+1\right)\left(\sqrt{n+1}+\sqrt{n}\right)}\)Chứng minh rằng: \(S_1+S_2+...+S_{2017}< \frac{2017}{2019}\)
Với mỗi số nguyên dương n, kí hiệu \(S_n\)là tổng n số nguyên tố đầu tiên.
\(S_1=2;S_2=2+3;S_3=2+3+5;.......\)
CMR trong dãy số \(S_1,S_2,S_3,......\)không tồn tại 2 số hạng liên tiếp đều là số chính phương
Cho \(S_n=\sqrt{1+\left(\frac{n+1}{n}\right)^2}+\sqrt{\frac{1}{n^2}-2\left(\frac{1}{n}-1\right)}\)Tính: \(\frac{1}{S_1}+\frac{1}{S_2}+...+\frac{1}{S_{2018}}\)
Cho \(S_n=\frac{1}{1.5}+\frac{1}{5.9}+\frac{1}{9.13}+...+\frac{1}{\left(4n-1\right)\left(4n+1\right)}n\in N^{ }\)*
a) Tính \(S_1,S_2,S_3,S_4\)
b) Hãy dự toán công thức Tính \(S_n\)và chứng minh bằng quy nạp
Bạn ghi đề bài sai thì phải, \(\frac{1}{\left(4n-1\right)\left(4n+1\right)}\) không hề phù hợp với các số hạng đầu tiên
Cho tổng \(S_n=\dfrac{1}{1.2}+\dfrac{1}{2.3}+.....+\dfrac{1}{n\left(n+1\right)}\) với \(n\in N^{\circledast}\) ?
a) Tính \(S_1,S_2,S_3\) ?
b) Dự đoán công thức tỉnh tổng \(S_n\) và chứng minh bằng quy nạp
a) Ta có:
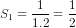
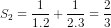
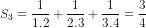
b) Từ câu a) ta dự đoán 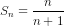 (1), với mọi n ε N* .
(1), với mọi n ε N* .
Ta sẽ chứng minh đẳng thức (1) bằng phương pháp quy nạp
Khi n = 1, vế trái là 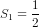 , vế phải bằng
, vế phải bằng 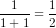 . Vậy đẳng thức (1) đúng.
. Vậy đẳng thức (1) đúng.
Giả sử đẳng thức (1) đúng với n = ≥ 1, tức là
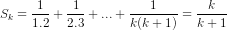
Ta phải chứng minh nó cũng đúng khi n = k + 1, nh=ghĩa là phải chứng minh
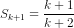
Ta có 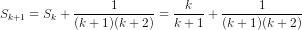
= 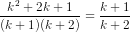
tức là đẳng thức (1) cũng đúng với n = k + 1.
Vậy điều cần chứng minh đúng với mọi n.
Cho \(S_n=\frac{1}{\sqrt{n^3}+\sqrt{n}}\)Chứng minh rằng: \(S_1+S_2+...+S_n< 2\)
\(\frac{1}{\sqrt{n}\left(n+1\right)}=\frac{\sqrt{n}}{n\left(n+1\right)}=\sqrt{n}\left(\frac{1}{n}-\frac{1}{n+1}\right)\)\(=\sqrt{n}\left(\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}\right)\left(\frac{1}{\sqrt{n}}+\frac{1}{\sqrt{n+1}}\right)< \sqrt{n}\left(\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}\right).\frac{2}{\sqrt{n}}\)\(=2\left(\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}\right)\)
=>\(S_1+...+S_n< 2\left(1-\frac{1}{\sqrt{n+1}}\right)< 2\)
Cho tổng :
\(S_n=\dfrac{1}{1.5}+\dfrac{1}{5.9}+\dfrac{1}{9.13}+....+\dfrac{1}{\left(4n-3\right)\left(4n+1\right)}\)
a) Tính \(S_1,S_2,S_3,S_4\)
b) Dự đoán công thức tính \(S_n\) và chứng minh bằng phương pháp quy nạp
a)
\(S_1=\dfrac{1}{1.5}=\dfrac{1}{5}\)
\(S_2=\dfrac{1}{1.5}+\dfrac{1}{5.9}=\dfrac{1}{4}\left(\dfrac{1}{1}-\dfrac{1}{5}\right)+\dfrac{1}{4}\left(\dfrac{1}{5}-\dfrac{1}{9}\right)\)
\(=\dfrac{1}{4}\left(1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}\right)=\dfrac{1}{4}\left(1-\dfrac{1}{9}\right)=\dfrac{2}{9}\).
\(S_3=\dfrac{1}{1.5}+\dfrac{1}{5.9}+\dfrac{1}{9.13}=\dfrac{1}{4}\left(1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{13}\right)\)
\(=\dfrac{1}{4}\left(1-\dfrac{1}{13}\right)=\dfrac{3}{13}\).
\(S_4=\dfrac{1}{1.5}+\dfrac{1}{5.9}+\dfrac{1}{9.13}+\dfrac{1}{13.17}\)\(=\dfrac{1}{4}\left(1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{17}\right)\)
\(=\dfrac{1}{4}\left(1-\dfrac{1}{17}\right)=\dfrac{4}{17}\).
b) Dự đoán công thức : \(S_n=\dfrac{1}{4}\left(1-\dfrac{1}{4n+1}\right)\).
Chứng minh bằng quay nạp:
Với \(n=1\): \(S_1=\dfrac{1}{1.5}=\dfrac{1}{5}\).
Vậy giả thiết quy nạp đúng với n = 1.
Giả sử điều cần chứng minh đúng với \(n=k\).
Nghĩa là: \(S_k=\dfrac{1}{4}\left(1-\dfrac{1}{4k+1}\right)\).
Ta sẽ chứng minh nó đúng với \(n=k+1\): \(S_{k+1}=\dfrac{1}{4}\left(1-\dfrac{1}{4\left(k+1\right)+1}\right)\)
Thật vậy:
\(S_{k+1}=S_k+\dfrac{1}{\left[4\left(k+1\right)-3\right].\left[4\left(k+1\right)+1\right]}\)
\(=\dfrac{1}{4}\left(1-\dfrac{1}{4k+1}\right)+\dfrac{1}{4}\left(\dfrac{1}{4\left(k+1\right)-3}-\dfrac{1}{4\left(k+1\right)+1}\right)\)
\(=\dfrac{1}{4}\left(1-\dfrac{1}{4k+1}\right)+\dfrac{1}{4}\left(\dfrac{1}{4k+1}-\dfrac{1}{4\left(k+1\right)+1}\right)\)
\(=\dfrac{1}{4}\left(1-\dfrac{1}{4\left(k+1\right)+1}\right)\).
Vậy điều cần chứng minh đúng với mọi n.