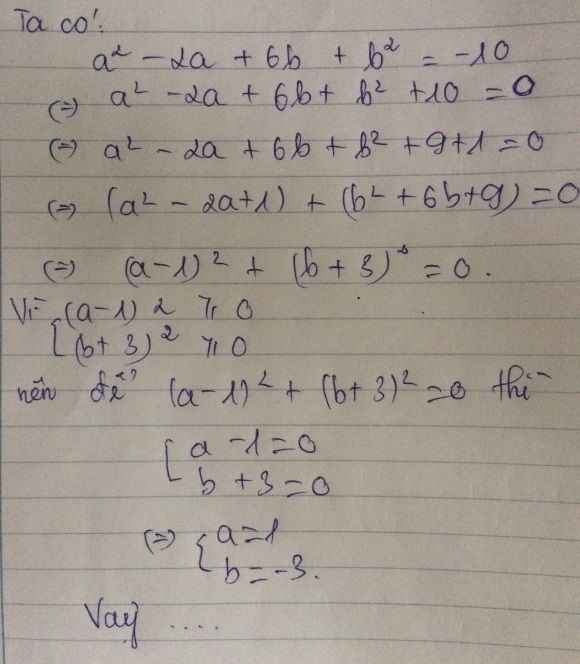tim a, b biet : a^2-2a+6b+b^2=-10
NN
Những câu hỏi liên quan
Tim gia tri cua A,b biet
A^2-2a+6b+b^2=-10
1a) a2 - 2a + 6b +b2=-10
<=> (a-1)2 +(b+3)2 =0
TA CÓ VẾ TRÁI LUÔN \(\ge\)0 VÌ TỔNG CÁC BÌNH PHƯƠNG LUÔN \(\ge\)0
DẤU = XÀY RA KHI a = 1 b = -3
b)X+Y/Z + Y+Z/X + Z+X/Y
<=>X+Y/Z +1 + Y+Z/X +1+ Z+X/Y+1 -3
<=>(X+Y+Z)(1/X+1/Y+1/Z)-3
TA CÓ 1/X +1/Y +1/Z=0
=> BT =-3
2A) QUY ĐỒNG CHUYỂN VẾ TA ĐƯỢC (A-B)^2>0
B) ÁP DỤNG BĐT CÔ SI x+y>= 2.CĂNxy
A+B>=2.\(\sqrt{ }\) AB
1/A +1/B>= 2.\(\sqrt{ }\) 1/AB
Đúng 0
Bình luận (0)
Ta có : \(a^2-2a+6b+b^2=-10\)
\(\Leftrightarrow a^2-2a+6b+b^2+10=0\)
\(\Leftrightarrow\left(a^2-2a+1\right)+\left(b^2+6b+9\right)=0\)
\(\Leftrightarrow\left(a-1\right)^2+\left(b+3\right)^2=0\left(1\right)\)
Vì : \(\left(a-1\right)^2\ge0;\left(b+3\right)^2\ge0\) với mọi \(a,b\)
Nên để thõa mãn đẳng thức \(\left(1\right)\) thì phải xảy ra đồng thời : \(\left(a-1\right)^2=0\) và \(\left(b+3\right)^2=0\)
\(\Leftrightarrow a-1=0\) và \(b+3=0\) \(\Leftrightarrow a=1\) và \(b=-3\)
Đúng 0
Bình luận (0)
tinh gia tri cua a,b biet_ 2a+6b+b2=-10
tim cac so a,b biet |5a-6b+300|^2007 +(2a-3b)^2008=0
\(\left|5a-6b+300\right|^{2007}+\left(2a-3b\right)^{2008}=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}5a-6b+300=0\\2a-3b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5a-6b=-300\\2a-3b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-300\\b=-200\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tim a,b,c biet: \(a^2+4b^2+9=2ab+3a+6b\)
\(a^2+4b^2+9=2ab+3a+6b\)
\(\Leftrightarrow2a^2+8b^2+18=4ab+6a+12b\)
\(\Leftrightarrow\left(a^2-4ab+4b^2\right)+\left(a^2-6a+9\right)+\left(4b^2-12b+9\right)=0\)
\(\Leftrightarrow\left(a-2b\right)^2+\left(a-3\right)^2+\left(2b-3\right)^2=0\) \(\Rightarrow\left\{{}\begin{matrix}\left(a-2b\right)^2=0\\\left(a-3\right)^2=0\\\left(2b-3\right)^2=0\end{matrix}\right.\)
(do \(\left(a-2b\right)^2\ge0;\left(a-3\right)^2=0;\left(2b-3\right)^2=0\) )
\(\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=\frac{3}{2}\end{matrix}\right.\) Vậy (a;b)=(3;3/2)
Đúng 0
Bình luận (0)
\(\Leftrightarrow2\left(a^2+4b^2+9\right)=2\left(2ab+3a+6b\right)\)
\(\Leftrightarrow2a^2+8b^2+18-4ab-6a-12b=0\)
\(\Leftrightarrow\left(a^2-4ab+4b^2\right)+\left(a^2-6a+9\right)+\left(4b^2-12b+9\right)=0\)
\(\Leftrightarrow\left(a-2b\right)^2+\left(a-3\right)^2+\left(2b-3\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(a-2b\right)^2=0\\\left(a-3\right)^2=0\\\left(2b-3\right)^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-2b=0\\a-3=0\\2b-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2b\\a=3\\b=\frac{3}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=\frac{3}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
tìm giá trị của a ,b biết a^2-2a+6b+b^2=-10
a2-2a+6b+b2=-10
⇒ a2-2a+6b+b2+10=0
⇒ (a2-2a+1)+(b2+6b+9)=0
⇒ (a-1)2+(b+3)2=0
vì (a-1)2≥ 0; (b+3)2 ≥ 0 mà (a-1)2+(b+3)2=0
⇒ a-1=0 và b-3=0
⇒ a=1,b=3
Đúng 1
Bình luận (0)
a2-2a+6b+b2=-10
<=> a2-2a+6b+b2+10=0
<=> a2-2a+1+6b+b2+9=0
<=> (a-1)2+(b+3)2=0
<=> (a-1)2=(b+3)2=0
\(<=>\left[\begin{array}{} (a-1)^2=0\\ (b+3)^2=0 \end{array} \right.\)
\(<=>\left[\begin{array}{} a-1=0\\ b+3=0 \end{array} \right.\)
\(<=>\left[\begin{array}{} a=1\\ b=-3 \end{array} \right.\)
Vậy a=1;b=-3
Đúng 0
Bình luận (1)
Tìm giá trị của a,b biết
a^2-2a+6b+b^2=-10
\(\Leftrightarrow a^2-2a+1+b^2+6b+9=0\)
\(\Leftrightarrow\left(a-1\right)^2+\left(b+3\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-1=0\\b+3=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-3\end{matrix}\right.\)
Đúng 3
Bình luận (0)
tim a,b (a>b>0) biet 2a^2+3b^2=7ab
Ta có: \(2a^2+3b^2=7ab\)
\(=>2a^2+3b^2-7ab=0\)
\(=>2a^2-7ab+3b^2=0\)
\(=>2a^2-6ab-ab+3b^2=0\)
\(=>2a\left(a-3b\right)-b\left(a-3b\right)=0\)
\(=>\left(2a-b\right)\left(a-3b\right)=0=>\orbr{\begin{cases}2a-b=0\\a-3b=0\end{cases}=>\orbr{\begin{cases}2a=b\\a=3b\end{cases}}}\)
Theo đề : a>b>0 nên 2a=b là vô lí
Do đó a=3b
->Có nhiều cặp số thỏa mãn a=3b
Đúng 0
Bình luận (0)
5/ tim 2 so a va b biet 2a = 3b va a- b=8
\(2a=3b\Rightarrow\frac{a}{2}=\frac{b}{3}\)
Áp dụng tính chất của dãy tỉ số bằng nhau có:
\(\frac{a}{2}=\frac{b}{3}=\frac{a-b}{2-3}=\frac{8}{-1}=-8\)
Có : \(\frac{a}{2}=-8\Rightarrow a=-16\)
Và \(\frac{b}{3}=-8\Rightarrow b=-24\)
Đúng 0
Bình luận (0)
\(2a=3b=>\frac{a}{2}=\frac{b}{3}\)
Áp dụng tính chất của dãy tỉ số bằng nhau là:
\(\frac{a}{2}=\frac{b}{3}=\frac{a-b}{2-3}=\frac{8}{-1}=-8\\ C\text{ó}:\frac{a}{2}=-8=>a=-16\\ V\text{à}\frac{b}{3}=-8=>b=-24\)
Đúng 0
Bình luận (0)
Vì 2a=3b\(\Rightarrow\frac{a}{3}=\frac{b}{2}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\Rightarrow\frac{a}{3}=\frac{b}{2}=\frac{a-b}{3-2}=\frac{8}{1}=8\)
\(\Rightarrow\begin{cases}\frac{a}{3}=8\\\frac{b}{2}=8\end{cases}\)\(\Rightarrow\begin{cases}a=24\\b=16\end{cases}\)
Vậy a=24;b=16
Đúng 0
Bình luận (0)
tim so A BIET 1/2A + 10=2/3A