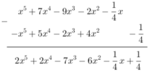`a,`

`F(x)=4x^4-2+2x^3+2x^4-5x+4x^3-9`

`F(x)=(2x^4+4x^4)+(2x^3+4x^3)-5x+(-2-9)`

`F(x)=6x^4+6x^3-5x-11`

`b,`

`K(x)=F(x)+G(x)`

`K(x)=(6x^4+6x^3-5x-11)+(6x^4+6x^3-x^2-5x-27)`

`K(x)=6x^4+6x^3-5x-11+6x^4+6x^3-x^2-5x-27`

`K(x)=(6x^4+6x^4)+(6x^3+6x^3)-x^2+(-5x-5x)+(-11-27)`

`K(x)=12x^4+12x^3-x^2-10x-38`

`c,`

`H(x)=F(x)-G(x)`

`H(x)=(6x^4+6x^3-5x-11)-(6x^4+6x^3-x^2-5x-27)`

`H(x)=6x^4+6x^3-5x-11-6x^4-6x^3+x^2+5x+27`

`H(x)=(6x^4-6x^4)+(6x^3-6x^3)+x^2+(-5x+5x)+(-11+27)`

`H(x)=x^2+16`

Đặt `x^2+16=0`

Ta có: \(x^2\ge0\text{ }\forall\text{ }x\)

`->`\(x^2+16\ge16>0\text{ }\forall\text{ }x\)

`->` Đa thức `H(x)` vô nghiệm.

Mình cần gấp lắm r, giúp mình với

a)\(f\left(x\right)=2x^2-x-3+5=\left(x+1\right)\left(2x-3\right)+5\)

Để \(f\left(x\right)⋮g\left(x\right)\Leftrightarrow\left(x+1\right)\left(2x-3\right)+5⋮\left(x+1\right)\)

\(\Leftrightarrow5⋮\left(x+1\right)\)

mà \(x+1\in Z\Rightarrow x+1\in U\left(5\right)=\left\{-1;1;5;-5\right\}\)

\(\Leftrightarrow x\in\left\{-2;0;4;-6\right\}\)

Vậy...

b) \(f\left(x\right)=3x^2-4x+6=\left(3x^2-4x+1\right)+5=\left(3x-1\right)\left(x-1\right)+5\)

Để \(f\left(x\right)⋮g\left(x\right)\Leftrightarrow\left(3x-1\right)\left(x-1\right)+5⋮\left(3x-1\right)\)

\(\Leftrightarrow5⋮\left(3x-1\right)\) mà \(3x-1\in Z\Rightarrow3x-1\in U\left(5\right)=\left\{-1;1;5;-5\right\}\)

\(\Leftrightarrow x\in\left\{0;\dfrac{2}{3};2;-\dfrac{4}{3}\right\}\) mà x nguyên\(\Rightarrow x\in\left\{0;2\right\}\)

Vậy...

c)\(f\left(x\right)=\left(-2x^3-7x^2-5x+2\right)+3\)\(=\left(-2x^3-4x^2-3x^2-6x+x+2\right)+3\)\(=\left[-2x^2\left(x+2\right)-3x\left(x+2\right)+\left(x+2\right)\right]+3\)

\(=\left(x+2\right)\left(-2x^2-3x+1\right)+3\)

Làm tương tự như trên \(\Rightarrow x+2\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)

\(\Leftrightarrow x\in\left\{-5;-3;-1;1\right\}\)

Vậy...

d)\(f\left(x\right)=x^3-3x^2-4x+3=x\left(x^2-3x-4\right)+3=x\left(x+1\right)\left(x-4\right)+3\)

Làm tương tự như trên \(\Rightarrow x+1\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)

\(\Rightarrow x\in\left\{-4;-2;0;2\right\}\)

Vậy...

Bài 1

Gợi ý bạn làm : Bạn thay \(x=-4;x=-3;x=0;x=1\) vào \(f\left(x\right);g\left(x\right)\)

\(\Rightarrow\) Nếu kết quả ra giống nhau thì là nghiệm , ra khác nhau thì không là nghiệm

VD : Thay \(x=-4\) vào \(f\left(x\right)\) và \(g\left(x\right)\)

\(f\left(-4\right)=4.\left(-4\right)^4-5\left(-4\right)^3+3.\left(-4\right)+2=1334\)

\(g\left(x\right)=-4.\left(-4\right)^4+5\left(-4\right)^3+7=-1337\)

Ra hai kết quả khác nhau 

\(\Rightarrow x=-4\) không là nghiệm

Bài 2

\(f\left(x\right)-g\left(x\right)=\left(-x^5+3x^2+4x+8\right)-\left(-x^5-3x^2+4x+2\right)\\ =-x^5+3x^2+4x+8+x^5+3x^2-4x-2\\ =\left(-x^5+x^5\right)+\left(3x^2+3x^2\right)+\left(4x-4x\right)+\left(8-2\right)\\ =6x^2+6\\ =x^2+1\\ =x^2+2.\dfrac{1}{2}x+\dfrac{1}{4}+\dfrac{3}{4}\\ =\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall x\)

\(\Rightarrow\) phương trình vô nghiệm 

a)

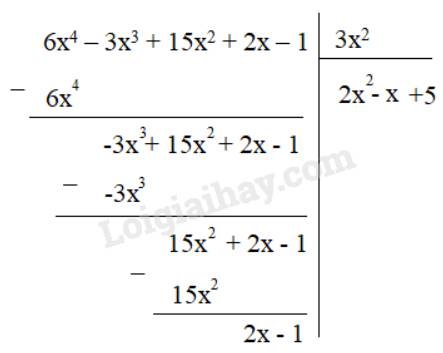
Thương Q(x) = 2x² – x + 5

Dư R(x) = 2x – 1

Ta có: F(x) = 3x² . (2x² – x + 5) + 2x – 1

b)

Thương Q(x) = 4x² + 2x – 2

Dư R(x) = -x – 1

Ta có: F(x) = (3x² + x + 1) . (4x² + 2x – 2) – x – 1

\(f\left(x\right)=x^3-x+7\)

\(g\left(x\right)=-x^3+8x-14\)

\(\Rightarrow f\left(x\right)+g\left(x\right)=7x-7\)

Nghiệm của đa thức \(f\left(x\right)+g\left(x\right)=0\Rightarrow7x-7=0\)

\(\Rightarrow x=1\)

f ) \(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)-24\)

\(=\left[\left(x+1\right)\left(x+4\right)\right]\left[\left(x+2\right)\left(x+3\right)\right]-24\)

\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24\)

Đặt \(x^2+5x+5=t\), ta có :

\(\left(t-1\right)\left(t+1\right)-24\)

\(=t^2-1-24=t^2-25\)

\(=\left(t-5\right)\left(t+5\right)\)

Thay và ta có :

\(\left(x^2+5x+5-5\right)\left(x^2+5x+5+5\right)\)

\(=\left(x^2+5x\right)\left(x^2+5x+10\right)\)

\(=x\left(x+5\right)\left(x^2+5x+10\right)\)

a) \(f\left(x\right)+g\left(x\right)+h\left(x\right)\)

\(=6x^7-5x^3+1-3+2x-4x^7-2x^7+2x+7x^2\)

\(=-5x^3+7x^2+4x-2\)

b) \(f\left(x\right)+g\left(x\right)-h\left(x\right)\)

\(=6x^7-5x^3+1-3+2x-4x^7-\left(-2x^7+2x+7x^2\right)\)

\(=2x^7-5x^3+2x-2+2x^7-2x-7x^2\)

\(=4x^7-5x^3-7x^2-2\)

b. Ta có f(x) + 2g(x)

= x3 - 2x2 + 2x- 5 + 2(-x3 + 3x2 - 2x + 4)

= x3 - 2x2 + 2x - 5 + (-2x3) + 6x2 - 4x + 8

=-x3 + 4x2 - 2x + 3 (0.5 điểm)

2f(x) - g(x) = x3 - 2x2 + 2x- 5 - 2(-x3+ 3x2 - 2x + 4)

= x3 - 2x2 + 2x - 5 + 2x3 - 6x2 + 4x - 8

= 3x3 - 8x2 + 6x - 13 (0.5 điểm)

c. Ta có f(x) + g(x)

=(x3 - 2x2 + 2x - 5) + (-x3 + 3x2 - 2x + 4) = x2 - 1

Ta có x2 - 1 = 0 ⇒ x2 = 1 ⇒ x = 1,x = -1

Vậy nghiệm của đa thức h(x) là x = ±1 (1 điểm)

* Ta có:

f(x) = x5 – 3x2 + 7x4 – 9x3 + x2 - 1/4 x

= x5 – (3x2 – x2) + 7x4 – 9x3 -1/4.x

= x5 – 2x2 + 7x4 – 9x3 -1/4.x

= x5 + 7x4 – 9x3 – 2x2 - 1/4

g(x) = 5x4 – x5 + x2 – 2x3 + 3x2 - 1/4

= 5x4 –x5+ (x2 + 3x2) – 2x3 – 1/4

= 5x4 – x5 + 4x2 – 2x3 – 1/4

= -x5 + 5x4 – 2x3 + 4x2 - 1/4

* f(x) + g(x)

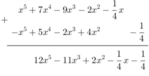
* f(x) - g(x)