X3- x -1 =0
Có nghiệm x0 CMR xo >0
Chứng minh rằng phương trình x 3 + x - 1 = 0 có nghiệm duy nhất x 0 thỏa mãn 0 < x 0 < 1 2
- Xét hàm số f ( x ) = x 3 + x - 1 , ta có f(0) = -1 và f(1) = 1 nên: f(0).f(1) < 0.
- Mặt khác: f ( x ) = x 3 + x - 1 là hàm đa thức nên liên tục trên [0;1].

- Suy ra f ( x ) = x 3 + x - 1 đồng biến trên R nên phương trình x 3 + x - 1 = 0 có nghiệm duy nhất x 0 ∈ ( 0 ; 1 ) .
- Theo bất đẳng thức Côsi:
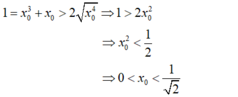
Bài 3: Với giá trị nào của k thì pt: a,2k2+kx-10=0, có 1 nghiệm x=2,b: [kx-5]x2 -[k-2]x+2k=0có 1 nghiệm x=-2 ,c,kx2-kx -72=0,có 1 nghiệm x=3
a: 2k^2+kx-10=0
Khi x=2 thì ta sẽ có: 2k^2+2k-10=0
=>k^2+k-5=0
=>\(k=\dfrac{-1\pm\sqrt{21}}{2}\)
b: Khi x=-2 thì ta sẽ có:
\(\left(-2k-5\right)\cdot4-\left(k-2\right)\cdot\left(-2\right)+2k=0\)
=>-8k-20+2k-4+2k=0
=>-4k-24=0
=>k=-6
c: Theo đề, ta có:
9k-3k-72=0
=>6k=72
=>k=12
Hàm số y = f(x) có đạo hàm trên khoảng K = x o - h ; x o + h h > 0 . Nếu f ' x 0 = 0 và f ' ' x 0 > 0 thì x 0 là
A. Điểm cực tiểu của hàm số.
B. Giá trị cực đại của hàm số.
C. Điểm cực đại của hàm số.
D. Giá trị cực tiểu của hàm số.
Đáp án là A
Theo điều đủ để hàm số có cực trị thì x 0 là điểm cực tiểu của hàm số.
Hỏi trên 0 ; π 2 , phương trình 2 sin 2 x − 3 sin x + 1 = 0 có bao nhiêu nghiệm?
A. 1
B.2
C . 3
D. 4
Phương trình 2 sin 2 x − 3 sin x + 1 = 0 ⇔ sin x = 1 2 sin x = 1
⇔ sin x = sin π 6 sin x = 1 ⇔ x = π 6 + k 2 π x = 5 π 6 + k 2 π x = π 2 + k 2 π k ∈ ℤ .
Theo giả thiết :
0 ≤ x < π 2 ⇔ 0 ≤ π 6 + k 2 π < π 2 0 ≤ 5 π 6 + k 2 π < π 2 0 ≤ π 2 + k 2 π < π 2 ⇔ − 1 12 < k < 1 6 → k ∈ ℤ k = 0 → x = π 6 − 5 12 < k < − 1 12 → k ∈ ℤ k ∈ ∅ − 1 4 < k < 0 → k ∈ ℤ k ∈ ∅ .
Vậy phương trình có duy nhất một nghiệm trên 0 ; π 2
Chọn đáp án A.
cho bất phương trình \(f\left(x\right)\le g\left(x\right),x_0\) là một nghiệm của bất phương trình \(f\left(x\right)\le g\left(x\right)\) nếu:
A. f(x0)=g(x0) đúng
B. f(x0) >= g(xo) đúng
C. f(x0) <= g(x0) sai
D. f(x0) > g(x0) đúng
1) cmr: Nếu x0 là nghiệm của đa thức P(x) = ax+b (a#0) thi P (x) = a. (x-x0)
x0 ở đây không phải x.0 đâu nha
2) tim gtnn:
A=( x+3)^2 +| y-2|
B=x^2 - 4x +2
3) CHO f(x)= 1+x+x^2 +x^3+.............+ x^2010 + x^2011. tinh f(1); f(-1)
4) cho đa thức H(x)= a. x^2+bx+c Biet 5a -3b+2c=0. cm: H(-1); H(-2)< OR = 0
P(x) = ax0+ b = 0 [Vì x0 là nghiệm của P(x)]
\(\Rightarrow ax_0=-b\Rightarrow b=-ax_0\)
Ta có:\(P\left(x\right)=ax+b\)
\(Thay:b=-ax_0\)
\(\Rightarrow P\left(x\right)=-ax_0+a=a.\left(x-x_0\right)\)
Akai HarumaMashiro ShiinaNguyễn Huy TúngonhuminhĐỗ Thanh Hải
help tui![]()
@ Nguyễn Chí Thành đây nè help![]()
Tìm hệ số của x 3 trong khai triển x = x 0 ⇔ f ' x 0 = 0 f ' ' x 0 > 0 thành đa thức?
A. 300
B.2300
C. 1200
D.18400
Cho các nhị thức bậc nhất f(x) = ax+b và g(x) =bx+a
Cmr: nếu x0 là nghiệm của f(x) thì 1/x0 là nghiệm của g(x)
Nếu x0 là một nghiệm của f(x) thì \(a.x_0+b=0\Rightarrow a=\dfrac{-b}{x_0}\)
Nếu \(x=\dfrac{1}{x_0}\)
\(\Rightarrow\dfrac{b}{x_0}+a=\dfrac{b}{x_0}+\left(-\dfrac{b}{x_0}\right)=0\)
\(\Rightarrowđpcm.\)
Hệ bất phương trình x + 3 5 - x > 0 x + 1 - m < 0 có nghiệm khi và chỉ khi
A. m<-2
B. m>-2
C. m<6
D. m>6