Giải pt bằng phương pháp đặt ẩn phụ
(5/x^2 -4x+5)-x^2+4x-1=0
Giải HPT bằng phương pháp đặt ẩn phụ
\(\left\{{}\begin{matrix}4x^2-3y^2=5\\x^2+2y^2=4\end{matrix}\right.\)
Đặt $x^2 = a > 0$ và $y^2 = b > 0$ thì hệ đã cho trở thành:
$\left\{\begin{aligned}&4a - 3b = 5\\&a + 2b = 4\\ \end{aligned}\right. \Leftrightarrow \left\{\begin{aligned}&4a - 3b = 5\\&a = 4 - 2b\\ \end{aligned}\right. \Leftrightarrow \left\{\begin{aligned}&16 - 8b - 3b = 5\\&a = 4 - 2b\\ \end{aligned}\right.$
$ \Leftrightarrow \left\{\begin{aligned}&- 11b = -11\\&a = 4 - 2b\\ \end{aligned}\right. \Leftrightarrow \left\{\begin{aligned}&b = 1 \, (tm)\\&a = 2 \, (tm)\\ \end{aligned}\right.$
Suy ra $x^2 = 2$ và $y^2 = 1$ từ đó em suy ra các nghiệm $(x;y)$ nhé
Giải các phương trình sau bằng phương pháp đặt ẩn phụ: x 2 - 2 x 2 – 2 x 2 + 4x – 3 = 0
Đặt m = x 2 – 2x
Ta có: x 2 - 2 x 2 – 2 x 2 + 4x – 3 = 0
⇔ x 2 - 2 x 2 – 2( x 2 – 2x) – 3 = 0
⇔ m 2 – 2m – 3 = 0
Phương trình m 2 – 2m – 3 = 0 có hệ số a = 1, b = -2, c = -3 nên có dạng a – b + c = 0
Suy ra: m 1 = -1, m 2 = 3
Với m = -1 ta có: x 2 – 2x = -1 ⇔ x 2 – 2x + 1 = 0
Phương trình x 2 – 2x + 1 = 0 có hệ số a = 1, b = -2, c = 1 nên có dạng a + b + c = 0
Suy ra: x 1 = x 2 = 1
Với m = 3 ta có: x 2 – 2x = 3 ⇔ x 2 – 2x – 3 = 0
Phương trình x 2 – 2x – 3 = 0 có hệ số a = 1, b = -2, c = -3 nên có dạng a – b + c = 0
Suy ra: x 1 = -1, x 2 = 3
Vậy phương trình đã cho có 3 nghiệm: x 1 = 1, x 2 = -1, x 3 = 3
gpt bằng phương pháp đặt ẩn phụ đưa về pt đẳng cấp:
\(\sqrt{5x^2-14x+9}-\sqrt{x^2-x+1}=2\left(x^2-4x+7\right)\sqrt{x-2}\)
Giải phương trình sau bằng cách đặt ẩn phụ:
\(\dfrac{x}{\sqrt{4x-1}}+\dfrac{\sqrt{4x-1}}{x}=2\)
Đặt \(\dfrac{x}{\sqrt{4x-1}}=a\)
Theo đề, ta có phương trình:
a+1/a=2
\(\Leftrightarrow a+\dfrac{1}{a}=2\)
\(\Leftrightarrow\dfrac{a^2+1-2a}{a}=0\)
=>a=1
=>\(x=\sqrt{4x-1}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2=4x-1\\x>=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-2\right)^2=3\\x>=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow x\in\left\{2+\sqrt{3};2-\sqrt{3}\right\}\)
3/ Giải phương trình bằng cách đặt ẩn phụ:
1. x2-|x|-2=0
2. x2+2x+|x+1|-5=0
3. x2+2x-5|x+1|+5=0
4. x2-2x+5|x-1|+5=0
5. x2-4x+2|x-2|+1=0
6. 4x2-20x+4|2x-5|+13=0
a/ Đặt \(\left|x\right|=t\ge0\Rightarrow t^2-t-2=0\Rightarrow\left[{}\begin{matrix}t=-1\left(l\right)\\t=2\end{matrix}\right.\)
\(\Rightarrow\left|x\right|=2\Rightarrow x=\pm2\)
b/ \(\Leftrightarrow\left(x+1\right)^2+\left|x+1\right|-6=0\)
Đặt \(\left|x+1\right|=t\ge0\Rightarrow t^2+t-6=0\Rightarrow\left[{}\begin{matrix}t=-3\left(l\right)\\t=2\end{matrix}\right.\)
\(\Rightarrow\left|x+1\right|=2\Rightarrow\left[{}\begin{matrix}x+1=2\\x+1=-2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
c/ \(\Leftrightarrow\left(x+1\right)^2-5\left|x+1\right|+4=0\)
Đặt \(\left|x+1\right|=t\ge0\Rightarrow t^2-5t+4=0\Rightarrow\left[{}\begin{matrix}t=1\\t=4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left|x+1\right|=1\\\left|x+1\right|=4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x+1=1\\x+1=-1\\x+1=4\\x+1=-4\end{matrix}\right.\)
d. \(\Leftrightarrow\left(x-1\right)^2+5\left|x-1\right|+4=0\)
Đặt \(\left|x+1\right|=t\ge0\Rightarrow t^2+5t+4=0\Rightarrow\left[{}\begin{matrix}t=-1\left(l\right)\\t=-4\left(l\right)\end{matrix}\right.\)
Vậy pt vô nghiệm
e. \(\Leftrightarrow\left(x-2\right)^2+2\left|x-2\right|-3=0\)
Đặt \(\left|x-2\right|=t\ge0\)
\(\Rightarrow t^2+2t-3=0\Rightarrow\left[{}\begin{matrix}t=1\\t=-3\left(l\right)\end{matrix}\right.\)
\(\Rightarrow\left|x-2\right|=1\Leftrightarrow\left[{}\begin{matrix}x-2=1\\x-2=-1\end{matrix}\right.\)
f. \(\Leftrightarrow\left(2x-5\right)^2+4\left|2x-5\right|-12=0\)
Đặt \(\left|2x-5\right|=t\ge0\)
\(\Rightarrow t^2+4t-12=0\Rightarrow\left[{}\begin{matrix}t=2\\t=-6\left(l\right)\end{matrix}\right.\)
\(\Rightarrow\left|2x-5\right|=2\Rightarrow\left[{}\begin{matrix}2x-5=2\\2x-5=-2\end{matrix}\right.\)
Giải các phương trình sau bằng phương pháp đặt ẩn phụ :
a) \(\left(x^2-2x\right)^2-2x^2+4x-3=0\)
b) \(3\sqrt{x^2+x+1}-x=x^2+3\)
Bài 1: Giải phương trình( đặt ẩn phụ)
a) \(\sqrt{4x^2-4x-11}=8x^2-8x-28\)
b)\(\sqrt{3x^2+9x+8}=x^2+3x-2\)
c) (x+5).(2-x) = \(\sqrt{x^2+3x}\)
d) \(\sqrt{x^2-4x+5}=x^2-4x+12\)
(mình đag cần gấp)
1/ ĐKXĐ: $4x^2-4x-11\geq 0$
PT $\Leftrightarrow \sqrt{4x^2-4x-11}=2(4x^2-4x-11)-6$
$\Leftrightarrow a=2a^2-6$ (đặt $\sqrt{4x^2-4x-11}=a, a\geq 0$)
$\Leftrightarrow 2a^2-a-6=0$
$\Leftrightarrow (a-2)(2a+3)=0$
Vì $a\geq 0$ nên $a=2$
$\Leftrightarrow \sqrt{4x^2-4x-11}=2$
$\Leftrightarrow 4x^2-4x-11=4$
$\Leftrightarrow 4x^2-4x-15=0$
$\Leftrightarrow (2x-5)(2x+3)=0$
$\Rightarrow x=\frac{5}{2}$ hoặc $x=\frac{-3}{2}$ (tm)
2/ ĐKXĐ: $x\in\mathbb{R}$
PT $\Leftrightarrow \sqrt{3x^2+9x+8}=\frac{1}{3}(3x^2+9x+8)-\frac{14}{3}$
$\Leftrightarrow a=\frac{1}{3}a^2-\frac{14}{3}$ (đặt $\sqrt{3x^2+9x+8}=a, a\geq 0$)
$\Leftrightarrow a^2-3a-14=0$
$\Rightarrow a=\frac{3+\sqrt{65}}{2}$ (do $a\geq 0$)
$\Leftrightarrow 3x^2+9x+8=\frac{37+3\sqrt{65}}{2}$
$\Rightarrow x=\frac{1}{2}(-3\pm \sqrt{23+2\sqrt{65}})$
3. ĐKXĐ: $x^2+3x\geq 0$
PT $\Leftrightarrow 10-(x^2+3x)=\sqrt{x^2+3x}$
$\Leftrightarrow 10-a^2=a$ (đặt $\sqrt{x^2+3x}=a, a\geq 0$)
$\Leftrightarrow a^2+a-10=0$
$\Rightarrow a=\frac{-1+\sqrt{41}}{2}$
$\Leftrightarrow x^2+3x=a^2=\frac{21-\sqrt{41}}{2}$
$\Rightarrow x=\frac{1}{2}(-3\pm \sqrt{51-2\sqrt{41}})$ (đều tm)
Giải các phương trình sau bằng cách đặt ẩn số phụ 4 x - 5 2 – 6(4x -5) +8 =0
Đặt m =4x -5
Ta có: 4 x - 5 2 – 6(4x -5) +8 =0 ⇔ m 2 -6m +8 =0
∆ ’ = - 3 2 -1.8 =9 -8=1 > 0
∆ ' = 1 = 1
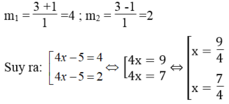
Vậy phương trình đã cho có 2 nghiệm x 1 =9/4 , x 2 =7/4
Tìm x (dùng phương pháp đặt ẩn phụ):
\(x^2+2x+5=\frac{5}{2}\sqrt{x^3+4x^2+5x+6}\)
ĐK: \(x^3+4x^2+5x+6\ge0\)
Ta có: \(x^3+4x^2+5x+6=\left(x+3\right)\left(x^2+x+2\right);x^2+2x+5=\left(x+3\right)+\left(x^2+x+2\right)\)
Đặt \(\hept{\begin{cases}\sqrt{x+3}=u\\\sqrt{x^2+x+2}=v\end{cases}}\)
Vậy nên ta có phương trình: \(\)\(u^2+v^2=\frac{5}{2}uv\)
\(\Leftrightarrow2u^2-5uv+2v^2=0\Leftrightarrow\orbr{\begin{cases}u=2v\\u=\frac{1}{2}v\end{cases}}\)
Với u = 2v ta có: \(\sqrt{x+3}=2\sqrt{x^2+x+2}\Leftrightarrow x+3=4x^2+4x+8\)
\(\Leftrightarrow4x^2+3x+5=0\) (Vô nghiệm)
Với \(u=\frac{1}{2}v\) ta có: \(2\sqrt{x+3}=\sqrt{x^2+x+2}\Leftrightarrow4x+12=x^2+x+2\)
\(\Leftrightarrow x^2-3x-10=0\Leftrightarrow\orbr{\begin{cases}x=5\\x=-2\end{cases}}\left(tmđk\right)\)
Vậy phương trình có nghiệm \(x\in\left\{5;-2\right\}\)