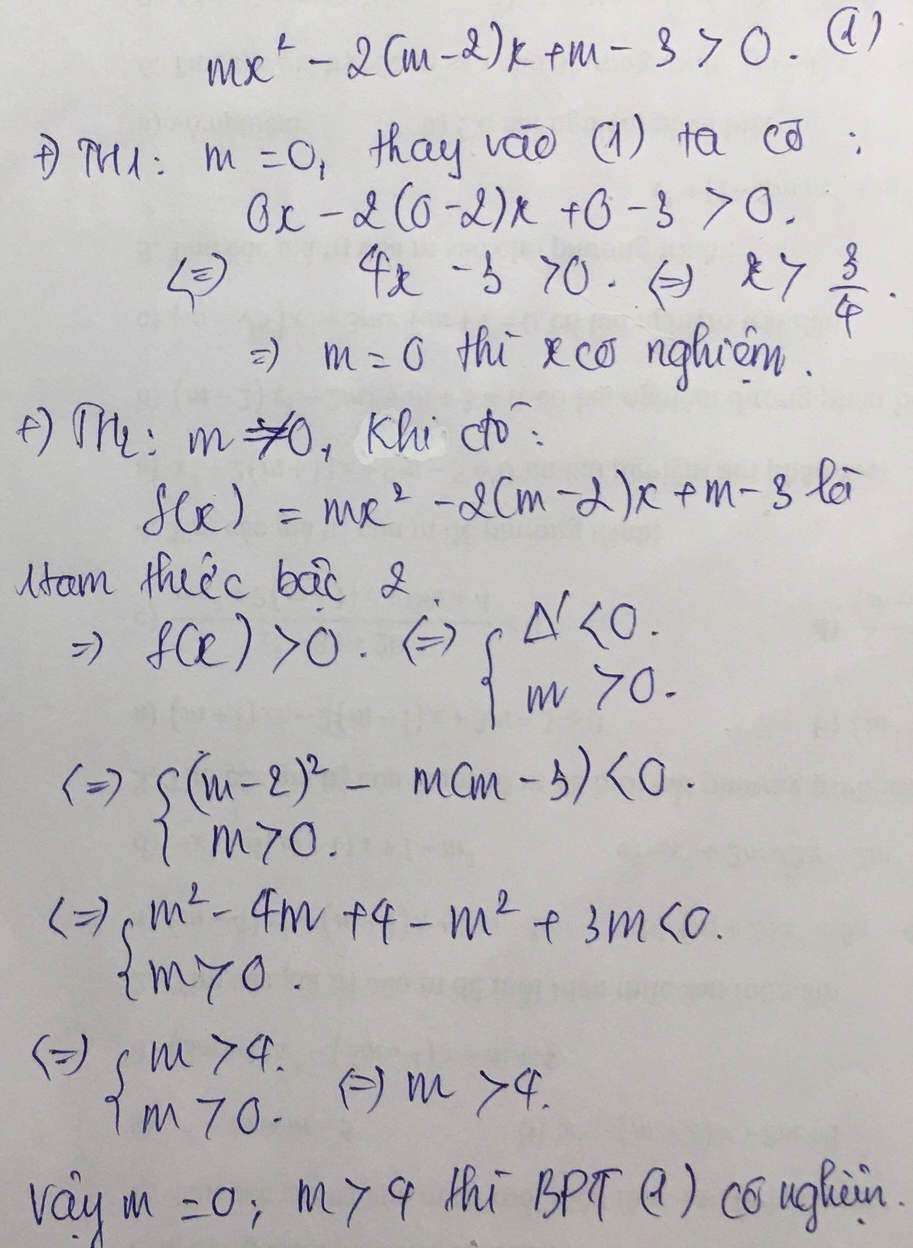Tìm m để bpt x+m>3 có nghiệm là {x|x>2}
H24
Những câu hỏi liên quan
1. Tìm nghiệm nguyên: \(\left\{{}\begin{matrix}y-\left|x^2-x\right|-1\ge0\\\left|y-2\right|+\left|x+1\right|-1\le0\end{matrix}\right.\)
2. Tìm m để bpt \(\left|\dfrac{x^2-mx-1}{x^2-2x+3}\right|\le1\) có tập nghiệm bằng R
3. Tìm m để bpt \(x^2+6x\le m\left(\left|x+3\right|+1\right)\) có nghiệm.
1.Tìm m để bpt \(2\left|x-m\right|+x^2+2>2mx\) thỏa mãn với mọi x
2. Tìm m để bpt : \(x^2+2\left|x+m\right|+2mx+3m^2-3m+1< 0\) có nghiệm
1.
\(2\left|x-m\right|+x^2+2>2mx\)
\(\Leftrightarrow\left(x-m\right)^2+2\left|x-m\right|-m^2+2>0\)
\(\Leftrightarrow t^2+2t-m^2+2>0\left(t=\left|x-m\right|\ge0\right)\)
\(\Leftrightarrow m^2< f\left(t\right)=t^2+2t+2\)
Yêu cầu bài toán thỏa mãn khi \(m^2< minf\left(t\right)=2\)
\(\Leftrightarrow-\sqrt{2}< m< 2\)
Vậy \(-\sqrt{2}< m< 2\)
Đúng 0
Bình luận (0)
2.
\(x^2+2\left|x+m\right|+2mx+3m^2-3m+1< 0\)
\(\Leftrightarrow\left(x+m\right)^2+2\left|x+m\right|+2m^2-3m+1< 0\)
\(\Leftrightarrow\left(\left|x+m\right|+1\right)^2< -2m^2+3m\)
Ta có \(VT=\left(\left|x+m\right|+1\right)^2=\left(-\left|x+m\right|-1\right)^2\le\left(-1\right)^2=1\)
Yêu cầu bài toán thỏa mãn khi \(VP=-2m^2+3m>1\)
\(\Leftrightarrow2m^2-3m+1< 0\)
\(\Leftrightarrow\dfrac{1}{2}< m< 1\)
Đúng 0
Bình luận (0)
Cho bpt \(\sqrt{x^2-3x+m}>2x+1\) tìm m để bpt có nghiệm x ∈\(\left[0;2\right]\)
Khi \(x\ge0\Rightarrow2x+1>0\) nên BPT tương đương:
\(x^2-3x+m>\left(2x+1\right)^2\)
\(\Leftrightarrow x^2-3x+m>4x^2+4x+1\)
\(\Leftrightarrow3x^2+7x+1< m\)
Xét hàm \(f\left(x\right)=3x^2+7x+1\) trên \(\left[0;2\right]\)
\(-\dfrac{b}{2a}=-\dfrac{7}{6}\notin\left[0;2\right]\) ; \(f\left(0\right)=1\) ; \(f\left(2\right)=27\)
\(\Rightarrow f\left(x\right)\ge1\Rightarrow\) pt có nghiệm trên đoạn đã cho khi \(m>1\)
Đúng 1
Bình luận (0)
tìm m để bpt \(x^2-2x+\left|x-1\right|+m\ge0\) có tập nghiệm là R
(key: \(m\ge1\))
Bpt \(\Leftrightarrow\left(x-1\right)^2+\left|x-1\right|+m-1\ge0;\forall x\)
Đặt \(t=\left|x-1\right|;t\ge0\)
Bpttt: \(t^2+t+m-1\)\(\ge0\) (1)
Để bpt có tập nghiệm là R khi (1) có nghiệm với mọi \(t\ge0\)
Đặt \(f\left(t\right)=t^2+t-1+m;t\ge0\) có đỉnh \(I\left(-\dfrac{1}{2};f\left(-\dfrac{1}{2}\right)\right)\)
\(\Rightarrow\) Hàm \(f\left(t\right)\) đồng biến trên \([0;+\infty)\)
Để \(f\left(t\right)\ge0;\forall t\ge0\)\(\Leftrightarrow\min\limits f\left(t\right)\ge0\)\(\Leftrightarrow f\left(0\right)\ge0\)\(\Leftrightarrow-1+m\ge0\Leftrightarrow m\ge1\)
Vậy...
Đúng 3
Bình luận (1)
tìm m để BPT : \(mx^2-2\left(m-2\right)x+m-3>0\) có nghiệm
Trường hợp 1: m=0
Bất phương trình trở thành:
\(-2\cdot\left(0-2\right)x+0-3>0\)
=>4x-3>0
hay x>3/4
=>Nhận trường hợp m=0
Trường hợp 2: m<>0
\(\text{Δ}=\left(2m-4\right)^2-4m\left(m-3\right)\)
\(=4m^2-16m+16-4m^2+12m\)
=-4m+16
Để phương trình có nghiệm thì \(\left\{{}\begin{matrix}-4m+16< 0\\m>0\end{matrix}\right.\Leftrightarrow m>4\)
Vậy: m>4
Đúng 1
Bình luận (2)
Với \(m=0\) thỏa mãn
Với \(m\ne0\) BPT vô nghiệm khi: \(mx^2-2\left(m-2\right)x+m-3\le0\) nghiệm đúng với mọi x
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\Delta'=\left(m-2\right)^2-m\left(m-3\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\-m+4\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\m\ge4\end{matrix}\right.\) \(\Rightarrow\) không tồn tại m để BPT đã cho vô nghiệm
\(\Rightarrow\) BPT đã cho có nghiệm với mọi m
Đúng 1
Bình luận (1)
1/ Tìm các giá trị của tham số m để bpt ( m-1) x^2- ( m-1) x+1>0 nghiệm đúng vs mọi giá trị của x. 2/ Tìm giá trị của tham số m để pt x^2 - ( m-2) x+m^2 -4m=0 có 2 nghiệm trái dấu. 3/ Tìm giá trị của tham số m để pt x^2 -mx+1=0 có 2 nghiệm phân biệt.
Bài 2:
Để phương trình có hai nghiệm trái dấu thì (m-2)(m+2)<0
hay -2<m<2
Đúng 0
Bình luận (0)
Tìm m để bpt sau có tập nghiệm là R: (m-4)x^2 +( 2m-8)x +m -5<0
Câu 1 : tìm m để BPT ( m - 1 )x2 + 2 ( m - 2 )x - 1 > 0 nghiệm đúng với mọi x ∈ R
Câu 2 : tìm m để BPT ( m - 1 )x2 + 2 ( m - 2 )x - 1 ≥ 0 vô nghiệm .
Giúp em với ạ . ThanksU <33
a, Yêu cầu bài toán thỏa mãn khi \(\left\{{}\begin{matrix}m-1>0\\\Delta'=m^2-4m+4+m-1< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>1\\\left(m-\dfrac{3}{2}\right)^2< -\dfrac{3}{4}\end{matrix}\right.\)
\(\Leftrightarrow\) vô nghiệm
Vậy không tồn tại giá trị m thỏa mãn
b, Yêu cầu bài toán thỏa mãn khi phương trình \(\left(m-1\right)x^2+2\left(m-2\right)x-1< 0\) có nghiệm với mọi x
\(\Leftrightarrow\left\{{}\begin{matrix}m-1< 0\\\Delta'=m^2-3m+3< 0\end{matrix}\right.\)
\(\Leftrightarrow\) vô nghiệm
Vậy không tồn tại giá trị m thỏa mãn
Đúng 1
Bình luận (0)
Câu 1 : các giá trị của m để tâm thức f(x)= x²-(m+2)x+8m+1 đổi dấu 2 lần
Câu 2 :Cho f(x)=-2x²+(m+2)x+m-4. Tìm M để f(x) âm với mọi x
Câu 3: bpt |x²-5x+4/x²-4|≥1 có nghiệm là :
Xem chi tiết