Các đường cao AN và BM của tam giác ABC có ba góc nhọn cắt nhau tại H và và cắt (O;R) ngoại tiếp tam giác ABC lần lượt tại D và E. a) Chứng minh CD = CE. b) Chứng minh H và D đối xứng nhau qua BC c) Chứng minh MN song song với DE d) Biết MN/AB = 1/2. Tính MN theo R
TT
Những câu hỏi liên quan
Các đường cao AN và BM của tam giác ABC có ba góc nhọn cắt nhau tại H và cắt đường tròn (O;R) ngoại tiếp tam giác ABC lần lượt tại D và E
Biết MN/AB =1/2 Tính MN theo R
Cho tam giác ABC có ba góc nhọn nội tiếp (O,R). Hai đường cao AN và BM của tam giác ABC cắt nhau tại I
a Chứng minh tứ giác IMCN nội tiếp được một đường tròn
b chứng minh IA.IN=IM.IB
c tia BM cắt (O) tại H Chứng minh AI=AH
a: góc INC+góc IMC=180 độ
=>INCM nội tiếp
b: Xét ΔINB vuông tại N và ΔIMA vuông tại M có
góc NIB=góc MIA
=>ΔINB đồng dạng với ΔIMA
=>IN/IM=IB/IA
=>IN*IA=IM*IB
c: góc AIH=góc BIN=góc BCA
=>góc AIH=góc AHI
=>AI=AH
Đúng 0
Bình luận (0)
Cho tam giác ABC có ba góc nhọn nội tiếp (O;R). Hai đường cao AN và BM của tam giác ABC cắt nhau tại I a) Chứng minh tứ giác IMCN nội tiêpa một đường tròn b) Chứng minh: IA.IN=IB.IM c) Tia BM cắt (O) tại H. Chứng minh AI = AH
a: góc INC+góc IMC=90+90=180 độ
=>IMCN nội tiếp
b: Xét ΔIMA vuông tại M và ΔINB vuông tại N có
góc MIA=góc NIB
=>ΔIMA đồng dạng với ΔINB
=>IM/IN=IA/IB
=>IM*IB=IN*IA
c: góc AHI=góc ACB
=>góc AHI=góc AIH
=>AH=AI
Đúng 0
Bình luận (0)
Cho tam giác ABC có ba góc nhọn nội tiếp (O;R). Hai đường cao AN và BM của tam giác ABC cắt nhau tại I a) Chứng minh tứ giác IMCN nội tiêpa một đường tròn b) Chứng minh: IA.IN=IB.IM c) Tia BM cắt (O) tại H. Chứng minh AI = AH
a: góc INC+góc IMC=90+90=180 độ
=>IMCN nội tiếp
b: Xét ΔIMA vuông tại M và ΔINB vuông tại N có
góc MIA=góc NIB
=>ΔIMA đồng dạng với ΔINB
=>IM/IN=IA/IB
=>IM*IB=IN*IA
c: góc AHI=góc ACB
=>góc AHI=góc AIH
=>AH=AI
Đúng 0
Bình luận (0)
giải giúp mình bài này với mình đang cần gấp
Cho tam giác ABC có ba góc nhọn nội tiếp (O,R). Hai đường cao AN và BM của tam giác ABC cắt nhau tại I
a Chứng minh tứ giác IMCN nội tiếp được một đường tròn
b chứng minh IA.IN=IM.IB
c tia BM cắt (O) tại H Chứng minh AI=AH
Giải thích các bước giải:
a) ΔABCΔABC có đường cao AN,BMAN,BM
⇒AN⊥BC;BM⊥AC⇒AN⊥BC;BM⊥AC
Xét tứ giác IMCNIMCN có:
ˆIMC=ˆINC=900(AN⊥BC;BM⊥AC;I∈AN;I∈BM)IMC^=INC^=900(AN⊥BC;BM⊥AC;I∈AN;I∈BM)
⇒ˆIMC+ˆINC=1800⇒IMC^+INC^=1800
⇒⇒ tứ giác IMCNIMCN nội tiếp
b) Xét ΔBINΔBIN và ΔAIMΔAIM có:
ˆBNI=ˆAMI=900(AN⊥BC;BM⊥AC;I∈AN;I∈BM)BNI^=AMI^=900(AN⊥BC;BM⊥AC;I∈AN;I∈BM)
ˆBIN=ˆAIMBIN^=AIM^ (đối đỉnh)
⇒⇒ ΔBIN∽ΔAIMΔBIN∽ΔAIM (g.g)
⇒IBIA=INIM⇒IA.IN=IM.IB⇒IBIA=INIM⇒IA.IN=IM.IB
c) Tứ giác IMCNIMCN nội tiếp
⇒ˆAIH=ˆNCM⇒AIH^=NCM^ hay ˆAIH=ˆACBAIH^=ACB^
Xét (O)(O) có: ˆACB=ˆAHBACB^=AHB^ (2 góc nội tiếp cùng chắn cung ABAB)
⇒ˆAIH=ˆAHB⇒AIH^=AHB^
⇒ˆAIH=ˆAHI⇒ΔAIH⇒AIH^=AHI^⇒ΔAIH cân tại A⇒AI=AH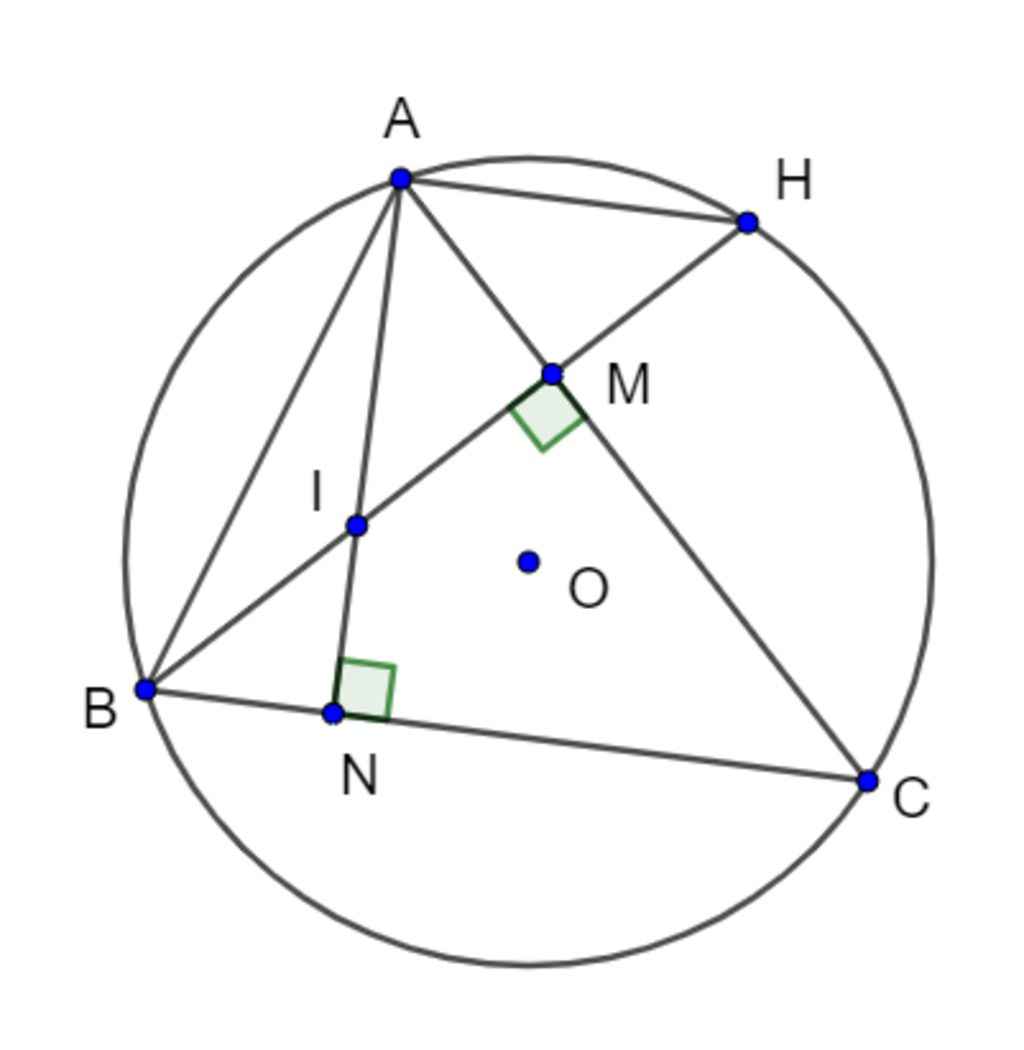
Đúng 0
Bình luận (0)
cho tam giác ABC có ba góc nhọn nội tiếp đường tròn(o). hai đường cao CE và AD cắt nhau tại H. Tia BO cắt (o) tại M, gọi I là giao điểm của BM và DE, K là giao điểm của AC và HM. Chứng minh CMID nội tiếp đường tròn
Các đườg cao AN và BM của tam giác ABC có 3 góc nhọn cắt nhau tại H và cắt đườg tròn (O; R ) ngoại tiếp tam giác ABC lần lượt tại D và E .
a) chứg minh CD = CE
b) chứg minh H và D đối xứng nhau qua BC
a, Xét từ giác AMNB ta có:
BM | AC => góc AMB =90
AN | BC => góc ANB =90
=> AMB = ANB
Mà: điểm M và N cùng nhìn 1 cạnh AB
=> AMNB nội tiếp => góc ABM = góc MBN
Hay: sđ cung EC =sđ cung DC
=> đpcm
b, Xét tứ giác MCNH , ta có:
góc HMC =90 và góc HNC =90
=> góc HMC + góc HNC =180
=> Tứ giác MCNH nội tiếp => góc HMN = góc HCN
Mà: góc HMN= góc NAB (cùng chắn cung BN)
Hay gócNAB = góc BCD (cùng chắn cung BD)
Từ trên suy ra: góc HCN = góc NCD
Xét 2 tam giác: tg HCN và tg NCD
góc HNC= góc CND = 90
NC chung
góc HCN = góc NCD
=> tg HCN = tg NCD (gcg)
=> HN=ND =>đpcm
Đúng 0
Bình luận (0)
cho an,bm là các đường cao của tam giác abc nhọn và cắt nhau tại h chúng cắt(o,r)ngoại tiếp tam giác abc tại d,e chứng minh
a,cd=ce
h đối xứng với d qua bc
c,mn//ed
Cho tam giác ABC có ba góc nhọn nội tiếp (O) ,các đường cao AD ,BE,CF cắt nhau tại H và cắt đường tròn lần lượt tại M,N,P
cm H và M đối xứng nhau qua AB
Sửa đề: M đối xứng H qua BC
Gọi AD là đường kính, I là giao của HD và BC
góc ABD=1/2*sđ cung AD=90 độ
=>BD//CH
góc ACD=1/2*sđ cung AD=90 độ
=>CD//BH
mà BD//CH
nên BHCD là hình bình hành
=>BC căt HD tại trung điểm của mỗi đường
=>I là trung điểm chung của HD và BC và BH//CD
góc AMD=1/2*sđ cung AD=90 độ
=>MD vuông góc AM
=>MD//BC
=>BCDM là hình thang cân
=>góc MBC=góc DCB=góc HBC
=>BC là phân giác của góc HBM
mà BC là trung tuyến của ΔHBM
nên ΔHMB cân tại B
=>BC là trug trực của MH
=>M đối xứng H qua BC
Đúng 1
Bình luận (0)
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn O các đường cao AM , BN cho tam giác ABC cắt nhau tại H và cắt đường tròn lần lượt tại D và E Chứng minh A, tứ giác MHNC nội tiếp đường tròn B, CD = CE C, CB là tia phân giác của góc HCD
a: góc HMC+góc HNC=180 độ
=>HMCN nội tiếp
b: góc CED=góc CAD
góc CDE=góc CAE
mà góc CAD=góc CAE(=góc CBD)
nên góc CED=góc CDE
=>CD=CE
Đúng 0
Bình luận (0)



