Điểm H là hình chiếu vuông gòc của M(3;-2) trên d:2x-3y+1=0. Khi đó
HA
Những câu hỏi liên quan
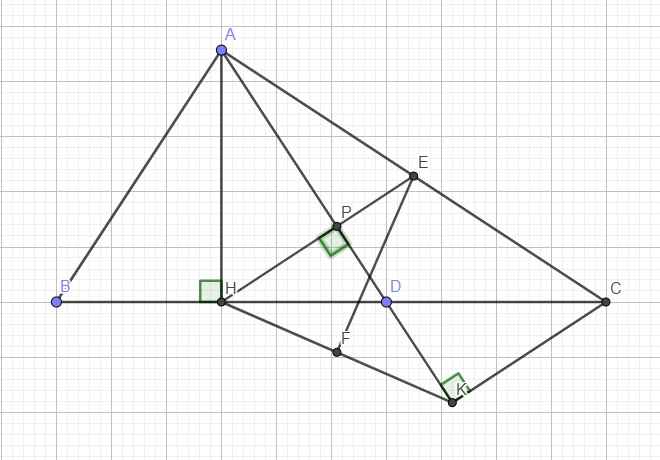
Cho tam giác ABC vuông cân tại A ,D là trung điểm của BC, lấy một điểm M thuộc đoạn AB( M khác A, M khác D). Gọi N,P lần lượt là hình chiếu vuông góc của M trên AB, AC và H là hình chiếu vuông góc của N trên PD. Chứng minh
a) 5 điểm A,N,M,H,P cùng thuộc một đường tròn
b) HN là phân Giác của góc AHM
c)H,M,B thẳng hàng
Cho điểm \(M\left( {{x_0};{y_0}} \right)\). Tìm tọa độ
a) Điểm H là hình chiếu vuông góc của M trên trục Ox
b) Điểm M’ đối xứng với M qua trục Ox
c) Điểm K là hình chiếu vuông góc của M trên trục Oy
d) Điểm M’’ đối xứng với M qua trục Oy
e) Điểm C đối xứng với M qua gốc tọa độ
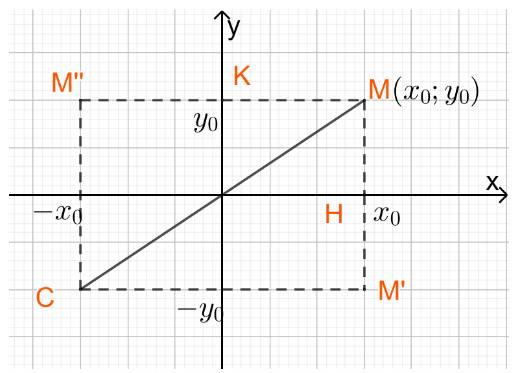
a) H là hình chiếu vuông góc của M trên trục Ox nên tọa độ điểm H là \(H\left( {{x_0};0} \right)\)
b) M’ đối xứng với M qua trục Ox nên H là trung điểm của MM’
Suy ra \({x_{M'}} = 2{x_H} - {x_M} = 2{x_0} - {x_0} = {x_0};{y_{M'}} = 2{y_H} - {y_M} = 2.0 - {y_0} = - {y_0}\)
Vậy tọa độ điểm M’ là \(\left( {{x_0}; - {y_0}} \right)\)
c) K là hình chiếu vuông góc của M trên trục Oy nên tọa độ điểm K là \(K\left( {0;{y_0}} \right)\)
d) M’’ đối xứng với M qua trục Oy nên K là trung điểm của MM’’
Suy ra \({x_{M''}} = 2{x_K} - {x_M} = 2.0 - {x_0} = - {x_0};{y_{M''}} = 2{y_K} - {y_M} = 2{y_0} - {y_0} = {y_0}\)
Vậy tọa độ điểm M'' là \(\left( { - {x_0};{y_0}} \right)\)
e) C đối xứng với M qua gốc tọa độ nên O là trung điểm của MC
Suy ra \({x_C} = 2{x_O} - {x_M} = 2.0 - {x_0} = - {x_0};{y_C} = 2{y_O} - {y_M} = 2.0 - {y_0} = - {y_0}\)
Vậy tọa độ điểm C là \(\left( { - {x_0}; - {y_0}} \right)\)
Đúng 0
Bình luận (0)
Cho tam gíac ABC vuông tại A, M là trung điểm của BC, H là hình chiếu của M trên AC, K là hình chiếu của H trên BC. Tính diện tích tam giác ABC biết MH=15mm, HK=12mm
Cho hình vuông ABCD và điểm M chạy trên cạnh BC. DM cắt tia AB tại K. Gọi H là hình chiếu của A trên DM.
a.chứng minh dh.dK Không đổi
b.xác định vị trí của điểm m để:
✳dh.dK nhỏ nhất
dh.dK=2a^2/3 nếu cạnh của hình vuông là a
Để chứng minh điều kiện dh.dK không đổi, ta sẽ sử dụng tính chất của hình chiếu. Gọi E là hình chiếu của M lên AB. Ta có thể thấy rằng tam giác ADE và tam giác AKH đồng dạng với nhau. Vì vậy, ta có thể sử dụng tỉ lệ đồng dạng để tính toán.
Giả sử cạnh của hình vuông là a. Khi đó, ta có AE = a - DM và AK = a - DH. Từ đó, ta có tỉ lệ đồng dạng sau:
AE/AK = DE/DH
(a - DM)/(a - DH) = DE/DH
Sau khi thực hiện phép tính, ta sẽ có:
DM = (2a^2)/3
Điểm M sẽ nằm ở vị trí để độ dài dh.dK đạt giá trị nhỏ nhất khi DM có giá trị như trên.
Còn về vị trí cụ thể của điểm M, để xác định nó, chúng ta cần thêm thông tin về vị trí của điểm M trên cạnh BC.
Đúng 0
Bình luận (0)
Cho đường thẳng d: x - 2y - 3 = 0. Tọa độ hình chiếu vuông góc H của điểm M(0;1) trên đường d là:
A. H(-1;2)
B. H(5;1)
C. H(3;0)
D. H(1;-1)
Chọn D.
Gọi Δ là đường thẳng đi qua M và vuông góc với đường thẳng d.
d: x - 2y - 3 = 0
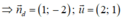
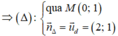
⇒ 2.(x - 0) + 1.(y - 1) = 0 ⇔ 2x + y - 1 = 0
Gọi H = d ∩ (Δ). Tọa độ điểm H là nghiệm của hệ phương trình:
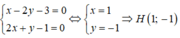
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC vuông tại A. Gọi H là hình chiếu vuông góc của A trên cạnh BC, D là điểm đối xứng của B qua H, K là hình chiếu vuông góc của C trên AD. Giả sử H (-5; -5), K (9; 3) và trung điểm của AC thuộc đường thẳng x - y + 10 = 0. Hoành độ điểm A là ?
Gọi E là trung điểm AC, do H và K cùng nhìn AC dưới 1 góc vuông nên H, K thuộc đường tròn đường kính AC (1)
\(\Rightarrow EH=EK\) hay E nằm trên trung trực HK
Gọi F là trung điểm HK \(\Rightarrow F\left(2;-1\right)\)
\(\overrightarrow{HK}=\left(14;-8\right)=2\left(7;-4\right)\Rightarrow\) EF nhận (7;-4) là 1 vtpt
Phương trình EF: \(7\left(x-2\right)-4\left(y+1\right)=0\Leftrightarrow7x-4y-18=0\)
Tọa độ E là nghiệm: \(\left\{{}\begin{matrix}x-y+10=0\\7x-4y-18=0\end{matrix}\right.\) \(\Rightarrow E\left(\dfrac{58}{3};\dfrac{88}{3}\right)\)
\(\widehat{ACH}=\widehat{HAK}\) (cùng phụ \(\widehat{ABC}\)) \(\Rightarrow AH=HK\)
Mà \(AE=EK\) theo (1) \(\Rightarrow AK\) là trung trực EH
\(\overrightarrow{HE}=\left(\dfrac{73}{3};\dfrac{103}{3}\right)=\dfrac{1}{3}\left(73,103\right)\) \(\Rightarrow AK\) nhận \(\left(103;-73\right)\) là 1 vtpt
Tới đây bạn hãy kiểm tra lại số liệu, số liệu quá bất hợp lý
Tính tiếp như sau:
Viết pt AK (biết đi qua K và có vtpt như trên)
Tìm tọa độ giao điểm P của EH và AK
Khi đó P là trung điểm AK, tìm tọa độ A dễ dàng bằng công thức trung điểm
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A , kẻ tia phân giác BD của góc ABC , kẻ AH vuông góc BC . Gọi E là giao điểm BD và AH, K là hình chiếu của H trên AN , Q là hình chiếu của H trên AC
C/m ; \(AH^2=BH.CH\)
cho hình chóp SABC. SA vuông góc với (ABC). AB=a,SA=a căn 3. Gọi H là hình chiếu của A lên SB. M là trung điểm của SC. Tính VSAHM/VSABC
\(SB=\sqrt{SA^2+AB^2}=2a\)
\(\dfrac{V_{SAHM}}{V_{SABC}}=\dfrac{SH}{SB}.\dfrac{SM}{SC}=\left(\dfrac{SA}{SB}\right)^2.\dfrac{SM}{SC}=\left(\dfrac{a}{2a}\right)^2.\dfrac{1}{2}=\dfrac{1}{8}\)
Đúng 1
Bình luận (0)
Cho Tam giác ABC vuông ở A có AB=9cm,BC=15cm lấy M là trung điểm của BC gọi H là hình chiếu vuông góc của M trên AB
a,Chứng minh H là trung điểm AB
b,Tính MH
\(a,\left\{{}\begin{matrix}BM=MC\\MH//AC\left(\perp AB\right)\end{matrix}\right.\Rightarrow AH=HB\) hay H là trung điểm AB
\(b,\left\{{}\begin{matrix}BM=MC\\AH=HB\end{matrix}\right.\Rightarrow MH\) là đtb tg ABC
\(\Rightarrow MH=\dfrac{1}{2}AC\)
Mà \(AC^2=BC^2-AB^2=144\left(pytago\right)\Rightarrow AC=12\left(cm\right)\)
\(\Rightarrow MH=6\left(cm\right)\)
Đúng 2
Bình luận (0)