Cho (d): x = t; y = 3t – 2, z = 4t +6 và △ : x - 5 1 = y + 1 - 4 = z - 20 1 . Chọn mệnh đề đúng .
B. d ⊥ ∆ d c 3 4 t ∆
PB
Những câu hỏi liên quan
Cho biểu thức D = (2x^2+1/x^3-1 - 1/x-1) : ( 1 - x^2+3/x^2+x+1)
a) Rút gọn D
b) Tìm giá trị của x để D = 3
c) Tìm những giá trị của x để D < 0
d) Tìm GTNN của biểu thức D biết x > 2
Xem chi tiết
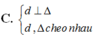
Cho biểu thức:
D=\(\frac{3\left(x+1\right)}{x^3+x^2+x+1}\)
a, tìm ĐKXĐ, rút gọn D
b, Tìm x để D nguyên
c, Tìm GTLN của D
a,ĐKXĐ của biểu thức D là :
x3+x2+x+1\(\ne0\)
\(\Leftrightarrow\)x2(x+1)+(x+1)\(\ne\)0
\(\Leftrightarrow\left(x+1\right)\left(x^2+1\right)\ne0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+1\ne0\\x^2+1\ne0\left(vôlí\right)\end{matrix}\right.\)
\(\Leftrightarrow x\ne-1\)
Ta có : D=\(\frac{3\left(x+1\right)}{x^3+x^2+x+1}=\frac{3\left(x+1\right)}{x^2\left(x+1\right)+\left(x+1\right)}=\frac{3.\left(x+1\right)}{\left(x+1\right)\left(x^2+1\right)}=\frac{3}{x^2+1}\)
b,Để D nguyên thì \(\frac{3}{x^2+1}\)(đkxđ: x\(\ne-1\)) nguyên
\(\Leftrightarrow\)x2+1\(\inƯ\left(3\right)=\left\{1;-1;3;-3\right\}\)
ta có bảng giá trị sau :
| x2+1 | -1 | 1 | 3 | -3 |
| x2 | -2 | 0 | 2 | -4 |
| x | ko có giá trị | 0 | \(\sqrt{2}\) | ko có giá trị |
| So sánh điều kiện | ko tm | tm | tm | ko tm |
vậy x\(\in\left\{0;\sqrt{2}\right\}\)thì D nguyên
c, Ta có : D=\(\frac{3}{x^2+1}\left(đkxđ:x\ne-1\right)\)\(\le3\)
Dấu = xảy ra khi : x=0 \(\Leftrightarrow\)D=3
Vậy Max D=3 \(\Leftrightarrow x=0\)
Đúng 0
Bình luận (0)
Cho \(D=\dfrac{x^3+x^2-2x}{x\left|x+2\right|-x^2+4}\)
a, Tìm điều kiện xác định và rút gọn D
b, Tìm x∈Z để D∈Z
c, Tính D khi x=6
a: ĐKXĐ: x|x+2|-x^2+4<>0
TH1: x>=-2
BPT sẽ là x^2+2x-x^2+4<>0
=>x<>-2
=>x>-2
TH2: x<-2
BPT sẽ là -x^2-2x-x^2+4<>0
=>-2x^2-2x+4<>0
=>x^2+x-2<>0
=>x<>-2; x<>1
=>x<-2
b: \(D=\dfrac{x\left(x+2\right)\left(x-1\right)}{x\left|x+2\right|-x^2+4}\)
TH1: x>-2
\(D=\dfrac{x\left(x+2\right)\left(x-1\right)}{x^2+2x-x^2+4}=\dfrac{x\left(x-1\right)}{2}\) luôn là só nguyên
TH2: x<-2
\(D=\dfrac{x\left(x+2\right)\left(x-1\right)}{-2x^2-2x+4}=\dfrac{-x\left(x+2\right)\left(x-1\right)}{2\left(x^2+x-2\right)}\)
\(=\dfrac{-x\left(x+2\right)\left(x-1\right)}{2\left(x+2\right)\left(x-1\right)}=\dfrac{-x}{2}\)
Để D nguyên thì x=2k
c: Khi x=6 thì \(D=\dfrac{6^3+6^2-2\cdot6}{6\left|6+2\right|-6^2+4}=15\)
Đúng 0
Bình luận (0)
Cho biết: \(D=\frac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\frac{\sqrt{x}+3}{\sqrt{x}-2}+\frac{2\sqrt{x}+1}{\sqrt{x}-3}\)
a, Rút gọn D.
b, Tính D khi x = \(\frac{1}{4}\).
c, Tìm x để D = 2.
d, Tìm x để D >3.
bài khá dễ nhưng làm thì mắc công quá
Đúng 0
Bình luận (0)
a) Rgọn
D= \(\frac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\frac{\sqrt{x}+3}{\sqrt{x}-2}+\frac{2\sqrt{x}+1}{\sqrt{x}-3}\)
= \(\frac{2\sqrt{x}-9-\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)+\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
=\(\frac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x-2}\right)\left(\sqrt{x}-3\right)}\)
=\(\frac{\sqrt{x}-1}{\sqrt{x}-3}\)
b)thay x=\(\frac{1}{3}\)ta dc
\(\frac{\sqrt{\frac{1}{4}}-1}{\sqrt{\frac{1}{4}-3}}\)=\(\frac{\frac{1}{2}-1}{\frac{1}{2}-3}\)=\(\frac{1}{2}\)
c) Để D=2 => \(\frac{\sqrt{x}-1}{\sqrt{x}-3}=2\)
=> 2\(\sqrt{x}-2=\sqrt{x}-3\)
=> \(\sqrt{x}=-1\)
=> x =1
Đúng 0
Bình luận (2)
Cho chất X t/d với một lượng vừa đủ dd NaOH, sau đó cô cạn dd thu được chất rắn Y và chất hữu cơ Z. Cho Z t/d với AgNO3 (hoặc Ag2O) trong dd NH3 thu được chất hữu cơ T. Cho chất T t/d với ddNaOH lại thu được chất Y. Chất X có thể là A. HCOOCHCH2. B. CH3COOCHCH2 C. HCOOCH3. D. CH3COOCHCH-CH3.
Đọc tiếp
Cho chất X t/d với một lượng vừa đủ dd NaOH, sau đó cô cạn dd thu được chất rắn Y và chất hữu cơ Z. Cho Z t/d với AgNO3 (hoặc Ag2O) trong dd NH3 thu được chất hữu cơ T. Cho chất T t/d với ddNaOH lại thu được chất Y. Chất X có thể là
A. HCOOCH=CH2.
B. CH3COOCH=CH2
C. HCOOCH3.
D. CH3COOCH=CH-CH3.
1.cho biểu thức
|D=(1/x-1-x/1-x^3-x^2+x+1/x+1):2x+1/x^2+x+1)
a)rút gọn D
b)tính gtri của D
c)tìm gtri nguyên của x để biểu thức D có gtri nguyên
1) cho P=\(\frac{x+y}{z+t}+\frac{y+z}{t+x}+\frac{z+t}{x+y}+\frac{t+x}{z+y}\)
tính P biết \(\frac{x}{y+z+t}=\frac{y}{z+t+x}=\frac{z}{y+x+t}=\frac{t}{x+y+z}\)
2) cho dãy tỉ số bằng : \(\frac{2a+b+c+d}{a}=\frac{a+2b+c+d}{b}=\frac{a+b+2c+d}{c}=\frac{a+b+c+2d}{d}\)
tính M=\(\frac{a+b}{c+d}+\frac{b+c}{d+a}+\frac{c+d}{a+b}+\frac{d+a}{c+b}\)
\(\frac{x}{y+z+t}=\frac{y}{z+t+x}=\frac{z}{y+x+t}=\frac{t}{x+y+z}=\frac{x+y+z+t}{2\left(x+y+z+t\right)}=\frac{1}{2}\)
=>2x=y+z+t
2y=x+z+t
2z+x+y+t
2t=x+y+z
=>x+y=2(z+t)(1)
y+z=2(x+t)(2)
z+t=2(x+y)(3)
t+x=2(y+z)(4)
Thay 1;2;3 và 4 vào P
=>P=2+2+2+2=8
bài 2 tương tự
Đúng 0
Bình luận (0)
Ác mộng làm sai thật rồi, bạn í chỉ có làm xong mỗi trường hợp x;y;t lớn hơn 0 thôi, còn trường hợp x;y;t nhỏ hơn 0 nữa
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho A=(x-1)(x+5)-x+1
B=4x+x^2
a) Tìm x để A=0.
b) Tính B/A.
c) Tính C/D biết: B/A+C/D=(5-x)/(1-x^2).
d) Tìm x nguyên để C/D có giá trị nguyên.
Cho hai đường thẳng
d
:
x
1
-
t
y
t
z
-
t
và
d
:...
Đọc tiếp
Cho hai đường thẳng d : x = 1 - t y = t z = - t và d ' : x = 2 t ' y = - 1 + t ' z = t ' . Khẳng định nào sau đây là đúng?
Cho biểu thức D=((x2+2)/(x3+1)-1/(x+1))*(4x/3)
a) Rút gọn biểu thức
b) Tính GTBT tại x=1/2
c) Tìm x để D=8/9
d) Tìm giá trị lớn nhất của D khi x>0
a: \(D=\left(\dfrac{x^2+2}{x^3+1}-\dfrac{1}{x+1}\right)\cdot\dfrac{4x}{3}\)
\(=\dfrac{x^2+2-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}\cdot\dfrac{4x}{3}\)
\(=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}\cdot\dfrac{4x}{3}\)
\(=\dfrac{4x}{3\left(x^2-x+1\right)}\)
b: Thay x=1/2 vào D, ta được:
\(D=\left(4\cdot\dfrac{1}{2}\right):\left[3\cdot\left(\dfrac{1}{4}-\dfrac{1}{2}+1\right)\right]\)
\(=2:\left[3\cdot\dfrac{1-2+4}{4}\right]\)
\(=2:\left[3\cdot\dfrac{3}{4}\right]=2:\dfrac{9}{4}=\dfrac{8}{9}\)
c: Ta có: D=8/9
nên \(\dfrac{4x}{3\left(x^2-x+1\right)}=\dfrac{8}{9}\)
\(\Leftrightarrow24\left(x^2-x+1\right)=36x\)
\(\Leftrightarrow2x^2-2x+2-3x=0\)
\(\Leftrightarrow2x^2-5x+2=0\)
=>(x-2)(2x+1)=0
=>x=2 hoặc x=-1/2
Đúng 1
Bình luận (0)