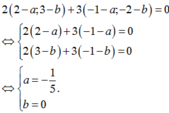Câu 1 : Trong mặt phẳng tọa độ Oxy ; cho (E) : x^2/a^2 + y^2/b^2 = 1 ( a > b > 0 ) . Một góc vuông uOv ( vuông tại O ) , cắt (E) tại M ; N . CMR : 1/OM^2 + 1/ON^2 ko đổi . Từ đó suy ra MN luôn tiếp xúc với 1 đường tròn cố định
HN
Những câu hỏi liên quan
(1) trong mặt phẳng tọa độ Oxy, cho hai vecto overrightarrow{a}left(1;-4right), overrightarrow{b}left(0;2right). tọa độ của vecto overrightarrow{u}2overrightarrow{a}-overrightarrow{b} là?(2) trong mặt phẳng tọa độ Oxy, cho hai vecto overrightarrow{a}left(-7;3right), overrightarrow{b}left(4;1right). tọa độ của vecto overrightarrow{u}overrightarrow{b}-2overrightarrow{a} là?(3) trong mặt phẳng tọa độ Oxy, cho hai vecto overrightarrow{u}left(-5;4right), overrightarrow{v}-3overrightarrow{j}. tọa độ c...
Đọc tiếp
(1) trong mặt phẳng tọa độ Oxy, cho hai vecto \(\overrightarrow{a}=\left(1;-4\right)\), \(\overrightarrow{b}=\left(0;2\right)\). tọa độ của vecto \(\overrightarrow{u}=2\overrightarrow{a}-\overrightarrow{b}\) là?
(2) trong mặt phẳng tọa độ Oxy, cho hai vecto \(\overrightarrow{a}=\left(-7;3\right)\), \(\overrightarrow{b}=\left(4;1\right)\). tọa độ của vecto \(\overrightarrow{u}=\overrightarrow{b}-2\overrightarrow{a}\) là?
(3) trong mặt phẳng tọa độ Oxy, cho hai vecto \(\overrightarrow{u}=\left(-5;4\right)\), \(\overrightarrow{v}=-3\overrightarrow{j}\). tọa độ của vecto \(\overrightarrow{a}=2\overrightarrow{u}-5\overrightarrow{v}\) là?
(4) trong mặt phẳng tọa độ Oxy, cho hai điểm A (1;1), B (4;-7) và \(\overrightarrow{OM}=2\overrightarrow{OA}-5\overrightarrow{OB}\). tổng hoành độ và tung độ của điểm M là?
giúp mk vs ạ mk cần gấp thank
(1); vecto u=2*vecto a-vecto b
=>\(\left\{{}\begin{matrix}x=2\cdot1-0=2\\y=2\cdot\left(-4\right)-2=-10\end{matrix}\right.\)
(2): vecto u=-2*vecto a+vecto b
=>\(\left\{{}\begin{matrix}x=-2\cdot\left(-7\right)+4=18\\y=-2\cdot3+1=-5\end{matrix}\right.\)
(3): vecto a=2*vecto u-5*vecto v
\(\Leftrightarrow\left\{{}\begin{matrix}a=2\cdot\left(-5\right)-5\cdot0=-10\\b=2\cdot4-5\cdot\left(-3\right)=15+8=23\end{matrix}\right.\)
(4): vecto OM=(x;y)
2 vecto OA-5 vecto OB=(-18;37)
=>x=-18; y=37
=>x+y=19
Đúng 0
Bình luận (0)
Chọn câu có khẳng định sai.Trong mặt phẳng tọa độ Oxy: A. Mọi điểm nằm trên trục tung đều có hoành độ bằng 0. B. Mọi điểm nằm trên trục hoành đều có tung độ bằng 0. C. Đồ thị của hàm số bậc nhất luôn đi qua gốc tọa độ O(0;0). D. Mọi điểm có hoành độ bằng tung độ thì nằm trên đường thẳng chứa tia phân giác của góc phần tư thứ nhất và thứ ba.
Đọc tiếp
Chọn câu có khẳng định sai.
Trong mặt phẳng tọa độ Oxy:
A. Mọi điểm nằm trên trục tung đều có hoành độ bằng 0.
B. Mọi điểm nằm trên trục hoành đều có tung độ bằng 0.
C. Đồ thị của hàm số bậc nhất luôn đi qua gốc tọa độ O(0;0).
D. Mọi điểm có hoành độ bằng tung độ thì nằm trên đường thẳng chứa tia phân giác của góc phần tư thứ nhất và thứ ba.
1.Trong mặt phẳng tọa độ Oxy cho hình bình hành ABCD với A (- 6;1); B (2;2) C (1;5) tọa độ đỉnh D là:
A. (5;2)
B. (-7;4)
C. (5;4)
D. (7;-4)
2.Trong mặt phẳng tọa độ Oxy cho tam giác ABC với A (- 1;3); B (2;1) C (5;5) tọa độ đỉnh D là của hình bình hành ABCD:
A. (0;4)
B. (8;1)
C. (8;3)
D. (-8;3)
Hướng dẫn em cách làm với ạ. Em cảm ơn nhiều.
1, Gọi tọa độ điểm D(x;y)
Ta có:\(\overrightarrow{AB}\left(8;1\right)\)
\(\overrightarrow{DC}\left(1-x;5-y\right)\)
Tứ giác ABCD là hình bình hành khi
\(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow1-x=8;5-y=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-7\\y=4\end{matrix}\right.\)
Vậy tọa độ điểm D(-7;4)
Đúng 1
Bình luận (1)
1. Trong mặt phẳng Oxy, có trọng tâm G(1,-1), M(2,1) và N(4,-2) lần lượt là trung điểm của AB, BC. Tìm tọa độ điểm B
2. Trong mặt phẳng Oxy, cho A(1,3), B(-2,2). Biết đường thẳng AB cắt trục tung tại điểm M(0,b). Giá trị b thuộc khoảng nào
3. Trong mặt phẳng tọa độ Oxy, cho A thỏa vecto OA 2vecto i + 3vecto j. Tọa độ điểm A là
4. Trong mặt phẳng Oxy, cho vecto x(1,2), vecto y(3,4), vecto z(5,-1). Tọa độ vecto u 2vecto x + vecto y - vecto z là
5. Trong mặt phẳng tọa độ Oxy, cho M(2,-3), N(4...
Đọc tiếp
1. Trong mặt phẳng Oxy, có trọng tâm G(1,-1), M(2,1) và N(4,-2) lần lượt là trung điểm của AB, BC. Tìm tọa độ điểm B
2. Trong mặt phẳng Oxy, cho A(1,3), B(-2,2). Biết đường thẳng AB cắt trục tung tại điểm M(0,b). Giá trị b thuộc khoảng nào
3. Trong mặt phẳng tọa độ Oxy, cho A thỏa vecto OA= 2vecto i + 3vecto j. Tọa độ điểm A là
4. Trong mặt phẳng Oxy, cho vecto x=(1,2), vecto y=(3,4), vecto z=(5,-1). Tọa độ vecto u = 2vecto x + vecto y - vecto z là
5. Trong mặt phẳng tọa độ Oxy, cho M(2,-3), N(4,7). Tọa độ trung điểm I của đoạn thẳng MN là
6. Cho vecto x=(-4,7) và hai vecto a=(2,-1), b=(-3,4). Nếu vecto x = m vecto a + n vecto b thì m, n là cặp số nào
1, Trong mặt phẳng tọa độ Oxy , cho M(1;-1) . N (3;2) , P(0;-5) lần lượt là trung điểm các cạnh BC, CA, AB của tam giác ABC Tìm tọa độ điểm A
2, Trong mặt phẳng tọa độ Oxy , cho A(1;3) , B(-1;-2) , C(1;5) . Tọa độ D trên trục Ox sao cho ABCD là hình thang có 2 đấy AB và CD là ?
Trong mặt phẳng tọa độ Oxy , cho B(2;3) , C(-1;-2) Điểm M thỏa mãn overrightarrow{2MB}+overrightarrow{3MC}overrightarrow{0} Tìm tọa độ điểm M
Trong mặt phẳng tọa độ Oxy , cho vecto overrightarrow{u}left(2;-4right),ove...
Đọc tiếp
1, Trong mặt phẳng tọa độ Oxy , cho M(1;-1) . N (3;2) , P(0;-5) lần lượt là trung điểm các cạnh BC, CA, AB của tam giác ABC Tìm tọa độ điểm A
2, Trong mặt phẳng tọa độ Oxy , cho A(1;3) , B(-1;-2) , C(1;5) . Tọa độ D trên trục Ox sao cho ABCD là hình thang có 2 đấy AB và CD là ?
Trong mặt phẳng tọa độ Oxy , cho B(2;3) , C(-1;-2) Điểm M thỏa mãn \(\overrightarrow{2MB}+\overrightarrow{3MC}=\overrightarrow{0}\) Tìm tọa độ điểm M
Trong mặt phẳng tọa độ Oxy , cho vecto \(\overrightarrow{u}=\left(2;-4\right),\overrightarrow{a}=\left(1;-2\right),\overrightarrow{b}=\left(1;-3\right)\)Biết \(\overrightarrow{u}=m\overrightarrow{a}+n\overrightarrow{b}\) tính m - n bẳng ?
Trong mặt phẳng tọa độ với hệ tọa độ Oxy, cho hai điểm A(-2,3), B(1,-6). Tọa độ vecto AB là?
\(\overrightarrow{AB}=\left(x_B-x_A;y_B-y_A\right)=\left(3;-9\right)\)
Đúng 0
Bình luận (0)
Câu 2. Trong mặt phẳng tọa độ Oxy, cho ba đường thẳng (d1):y=x+2 (d2):y=-x+4 và (d_{3}):y=mx+m. (m là tham số thục). a) Vẽ (d1) và (d2) trên cùng một mặt phẳng tọa độ Oxy. b) Xác định các giá trị của tham số m để đường thẳng (d3) đi qua giao điểm của (d1)và(d2)
a: 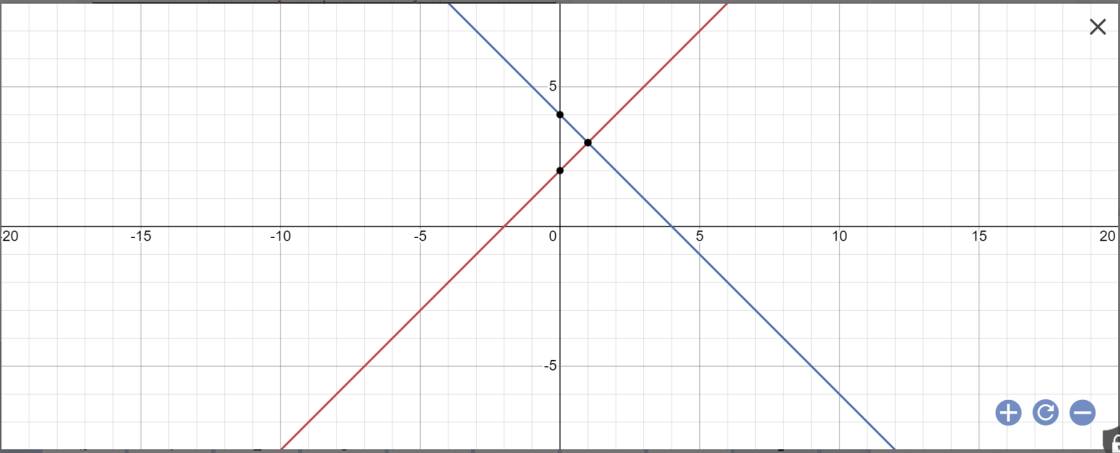
b: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}x+2=-x+4\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=2\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1+2=3\end{matrix}\right.\)
Thay x=1 và y=3 vào (d3), ta được:
\(1\cdot m+m=3\)
=>2m=3
=>\(m=\dfrac{3}{2}\)
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz hình chiếu của điểm M(1;-3;5) trên mặt phẳng (Oxy) có tọa độ là
A. (1;-3;5)
B. (1;-3;0)
C. (1;-3;1)
D. (1;-3;2)
Trong mặt phẳng tọa độ Oxy, cho B(2;3),C(-1;-2) Điểm M thỏa mãn
2
M
B
→
+
3
M
C
→
0
→
Tọa độ điểm M là A. M(1/5;0) B. M(-1/5;0) C. M(0;1/5) D. M(0;-1/5)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho B(2;3),C(-1;-2) Điểm M thỏa mãn 2 M B → + 3 M C → = 0 → Tọa độ điểm M là
A. M(1/5;0)
B. M(-1/5;0)
C. M(0;1/5)
D. M(0;-1/5)
Câu hỏi: Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2;3) và B(-1;2). Tìm N để A,B,N thẳng hàng.
Có vô số điểm N để A,B,N thẳng hàng, cho nên để tìm ra 1 điểm N cụ thể thì cần thêm điều kiện nữa (ví dụ N thuộc Ox, Oy hoặc đường thẳng nào đó)
Đúng 1
Bình luận (1)