Qua A nằm ngoài (O) kẻ 2 cát tuyến ABC,ADE tới (O) (B nằm giữa A và C; D nằm giữa A và E ). Kẻ dây BF//DE C/m
a) \(\widehat{DBF}=\widehat{DBC}\)
b) \(\Delta ACE=\Delta DCF\)Qua A nằm ngoài (O) kẻ 2 cát tuyến ABC,ADE tới (O) (B nằm giữa A và C; D nằm giữa A và E ). Kẻ dây BF//DE C/m
a) \(\widehat{DBF}=\widehat{DBC}\)
b)\(\Delta ACE=\Delta DCF\)
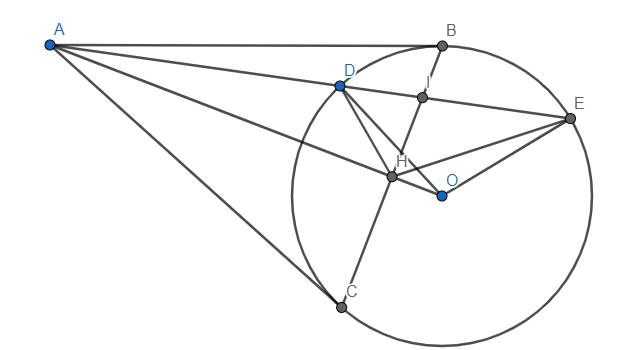
Cho đường tròn (O), điểm A nằm ngoài đường tròn (O). Kẻ hai cát tuyến ABC, ADE (với B nằm giữa A và C, D nằm giữa A và E, cát tuyến ABC nằm khác phía với cát tuyến ADE bờ AO). Gọi F là điểm di động trên cung nhỏ BD của (O) (F khác B và D). Vẽ (I) là tâm đường tròn ngoại tiếp tam giác AFB, (J) là tâm đường tròn ngoại tiếp tam giác AFD.
a) IO cắt BF tại K, JO cắt BF tại L. Chứng minh tứ giác OKFL nội tiếp một đường tròn.
b) IJ cắt AF tại M. Chứng minh: AC. MK = AE. ML
c) CJ cắt EI tại N. Chứng minh: N nằm trên đường tròn tâm O.
Cho đường tròn (O;R) và điểm A nằm ngoài đường tròn. Qua A kẻ 2 tiếp tuyến AB, AC với đường tròn (B,C là các tiếp điểm)
a) Chứng minh: 4 điểm A,B,O,C cùng thuộc một đường tròn
b) Kẻ cát tuyến ADE nằm giữa AO và AB (D nằm giữa A và E), kẻ các tiếp tuyến tại D và E cắt nhau tại S. Nối BC cắt OA tại H. Chứng minh: R^2=OH.OA và 3 điểm S, B,C thẳng hàng
a: Xét tứ giác ABOC có \(\widehat{ABO}+\widehat{ACO}=90^0+90^0=180^0\)
nên ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc một đường tròn
b: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AO là đường trung trực của BC
=>AO\(\perp\)BC tại trung điểm H của BC
Gọi K là giao điểm của OS và ED
Xét (O) có
SE,SD là các tiếp tuyến
Do đó: SE=SD
=>S nằm trên đường trung trực của ED(3)
Ta có: OE=OD
=>O nằm trên đường trung trực của ED(4)
Từ (3) và (4) suy ra SO là đường trung trực của ED
=>SO\(\perp\)ED tại trung điểm K của ED
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2=R^2\left(5\right)\)
Xét ΔODS vuông tại D có DK là đường cao
nên \(OK\cdot OS=OD^2=R^2\left(6\right)\)
Từ (5) và (6) suy ra \(OH\cdot OA=OK\cdot OS\)
=>\(\dfrac{OH}{OK}=\dfrac{OS}{OA}\)
Xét ΔOHS và ΔOKA có
\(\dfrac{OH}{OK}=\dfrac{OS}{OA}\)
góc HOS chung
Do đó: ΔOHS đồng dạng với ΔOKA
=>\(\widehat{OHS}=\widehat{OKA}\)
=>\(\widehat{OHS}=90^0\)
=>HO\(\perp\)SH tại H
mà HO\(\perp\)BH tại H
và SH,BH có điểm chung là H
nên S,H,B thẳng hàng
mà H,B,C thẳng hàng
nên S,B,H,C thẳng hàng
=>S,B,C thẳng hàng
Từ một điểm A nằm ngoài đường tròn (O). Kẻ 2 tiếp tuyến AB, AC (B, C là các tiếp điểm). Gọi H là giao điểm của 2 đường thẳng AO và BC. Qua A kẻ cát tuyến ADE với (O) (D, E thuộc (O)), sao cho tia AE nằm giữa 2 tia AO, AC và AD
Từ điểm \(A\) ở ngoài đường tròn \(\left(O\right)\), kẻ hai tiếp tuyến \(AB\), \(AC\) với đường tròn \(\left(O\right)\) (\(B\), \(C\) là hai tiếp điểm). Kẻ cát tuyến \(ADE\) với \(\left(O\right)\) không đi qua \(O\) (\(D\) nằm giữa \(A\) và \(E\)). Gọi \(H\) là giao điểm của \(OA\) và \(BC\).
\(a\)) Chứng minh \(OD^2=OH\cdot OA\). Từ đó suy ra tam giác \(OHD\) đồng dạng với tam giác \(ODA\).
\(b\)) Gọi \(I\) là giao điểm của \(BC\) và \(AE\). Chứng minh \(HI\) là phân giác của góc \(DHF\).
a) Do AB, AC tiếp xúc (O) tại B, C nên \(\widehat{OBA}=90^o\) và \(OA\perp BC\) tại H.
Xét tam giác OAB vuông tại B có đường cao BH, ta có \(OB^2=OA.OH\)
Mà \(OB=OD\left(=R_{\left(O\right)}\right)\) nên \(OD^2=OA.OH\). Từ đó suy ra \(\dfrac{OD}{OA}=\dfrac{OH}{OD}\). Từ đó dễ dàng suy ra 2 tam giác OHD và ODA đồng dạng.
b) Tam giác OAB vuông tại B có đường cao BH nên \(AB^2=AH.AO\)
Mặt khác, ta có \(\widehat{ABD}=\widehat{AEB}\) vì chúng lần lượt là góc tạo bởi tiếp tuyến, dây cung và góc nội tiếp cùng chắn cung BD.
\(\Rightarrow\Delta ABD~\Delta AEB\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AE}=\dfrac{AD}{AB}\Rightarrow AB^2=AD.AE\)
Từ đó suy ra \(AH.AO=AD.AE\) hay \(\dfrac{AH}{AD}=\dfrac{AE}{AO}\). Do đó \(\Delta AHE~\Delta ADO\left(c.g.c\right)\) \(\Rightarrow\widehat{AEH}=\widehat{AOD}\) hay tứ giác OHDE nội tiếp.
\(\Rightarrow\widehat{AHD}=\widehat{DEO}=\widehat{ODE}=\widehat{OHE}\)
\(\Rightarrow90^o-\widehat{AHD}=90^o-\widehat{OHE}\) \(\Rightarrow\widehat{DHI}=\widehat{EHI}\).
Ta suy ra được đpcm.
Từ một điểm A nằm bên ngoài (O),kẻ tiếp tuyến AB và cát tuyến ACD đi qua tâm O của đường tròn (C nằm giữa A và D).Tính góc BAD+2(góc ABC)
A.600 B.900 c.120o D.150o
Cho đường tròn (O ; R), và điểm A nằm ngoài đường tròn (O), kẻ tiếp tuyến AB AC. Kẻ cát tuyến ADE với đường tròn (O) (D nằm giữa A và E ; tia AE nằm giữa 2 tia AB và AO).
a) Vẽ hình
b) Chứng minh : AO vuông góc BC
c) Kẻ đường kinh BN.Chứng minh : CN//AO
cíu zứi
a:
b: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AO là đường trung trực của BC
=>AO\(\perp\)BC
c: Xét (O) có
ΔBCN nội tiếp
BN là đường kính
Do đó: ΔBCN vuông tại C
=>BC\(\perp\)CN
Ta có: BC\(\perp\)CN
BC\(\perp\)OA
Do đó: OA//CN
1. Cho (O; R) cố định và điểm A thay đổi nằm ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với (O) (với B, C là các tiếp điểm). Vẽ cát tuyến ADE với (O) (D nằm giữa A và E ; DE không đi qua O). Gọi H là giao điểm của AO và BC.
a. Chứng minh rằng tứ giác ABOC nội tiếp đường tròn.
b. Chứng minh rằng AH.AO = AD.AE và tứ giác DEOH là tứ giác nội tiếp.
c. Qua O vẽ đường thẳng vuông góc với AO cắt các tia AB, AC lần lượt tại M, N. Tìm vị trí của điểm A ở ngoài (O) để diện tích tam giác AMN đạt giá trị nhỏ nhất.
a) Xét tứ giác ABOC có
\(\widehat{ABO}\) và \(\widehat{ACO}\) là hai góc đối
\(\widehat{ABO}+\widehat{ACO}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ABOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABO vuông tại B có BH là đường cao ứng với cạnh huyền OA, ta được:
\(AH\cdot AO=AB^2\)(1)
Xét (O) có
\(\widehat{ABD}\) là góc tạo bởi tiếp tuyến BA và dây cung BD
\(\widehat{BED}\) là góc nội tiếp chắn \(\stackrel\frown{BD}\)
Do đó: \(\widehat{ABD}=\widehat{BED}\)(Hệ quả góc tạo bởi tiếp tuyến và dây cung)
hay \(\widehat{ABD}=\widehat{AEB}\)
Xét ΔABD và ΔAEB có
\(\widehat{ABD}=\widehat{AEB}\)
\(\widehat{BAD}\) chung
Do đó: ΔABD∼ΔAEB(g-g)
Suy ra: \(\dfrac{AB}{AE}=\dfrac{AD}{AB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB^2=AE\cdot AD\)(2)
Từ (1) và (2) suy ra \(AH\cdot AO=AD\cdot AE\)(đpcm)
Qua điểm A nằm ngoài đường tròn (O) Kẻ tiếp tuyến AM,AN với M,N là tiếp điểm. a) CMR: bốn điểm A,M,O,N cùng thuộc 1 đường tròn. b) Vẽ cát tuyến ABC tới (O) sao cho tia AO nằm giữa tia AM và tia AC.Chứng minh rằng: AM2 = = AB.AC c) Gọi H là giao điểm của AO và MN.CMR: 4 điểm B,H,O,C cùng thuộc một đường tròn. d) CMR: HN là tia phân giác của góc BHC.
a) Xét tứ giác OMAN có
\(\widehat{OMA}\) và \(\widehat{ONA}\) là hai góc đối
\(\widehat{OMA}+\widehat{ONA}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: OMAN là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
hay O,M,A,N cùng thuộc một đường tròn(đpcm)
Từ điểm A nằm ngoài đường tròn (O) kẻ 2 tiếp tuyến AB, AC đến (O) (B, C là 2 tiếp điểm). Kẻ cát tuyến ADE với (O) (D nằm giữa A và E). Gọi H là giao điểm của BC và OA
a) Cmr \(\Delta OHD\) đồng dạng với \(\Delta ODA\)
b) Cmr BC là tia phân giác của \(\widehat{DHE}\)
c) Từ D kẻ đường thẳng // BE cắt AB, AC lần lượt tại M, N. Cmr D là trung điểm của MN
\(a,\) Ta có \(OB=OC=R;AB=AC\Rightarrow OA\) là trung trực BC
Do đó \(OA\bot BC=\left\{H\right\}\)
Áp dụng HTL: \(OB^2=OH\cdot OA\Rightarrow OD^2=OH\cdot OA\Rightarrow\dfrac{OD}{OH}=\dfrac{OA}{OD}\)
\(\Rightarrow\Delta OHD\sim\Delta ODA\left(c.g.c\right)\)
\(b,\) Gọi \(\left\{I\right\}=BC\cap AE\)
\(\widehat{OHD}=\widehat{ODA}\Rightarrow\widehat{DHA}=\widehat{ODE}=\widehat{OED}\) (cùng bù với 2 góc bằng nhau, \(\Delta ODE\) cân tại O)
\(\Rightarrow\Delta AEO\sim\Delta AHD\left(g.g\right)\\ \Rightarrow\widehat{AOE}=\widehat{ADH}\)
Mà \(\dfrac{OH}{DH}=\dfrac{OD}{AD}\left(\Delta OHD\sim\Delta ODA\right)\Rightarrow\dfrac{OH}{DH}=\dfrac{OE}{AD}\)
\(\Rightarrow\Delta HEO\sim\Delta HDA\left(g.g\right)\\ \Rightarrow\widehat{OHE}=\widehat{DHA}\)
Mà \(OA\bot BC\Rightarrow\widehat{IHE}=\widehat{IHD}\)
Vậy BC trùng với p/g \(\widehat{DHE}\)
\(c,\) Vì HI là p/g trong của \(\Delta DHE\) và \(HA\bot HI\)
\(\Rightarrow HA\) là p/g ngoài
\(\Rightarrow\dfrac{IE}{ID}=\dfrac{AE}{AD}=\dfrac{HE}{HD}\left(1\right)\)
Mà \(MN\text{//}BE\Rightarrow\dfrac{MD}{BE}=\dfrac{AD}{AE};\dfrac{ND}{BE}=\dfrac{ID}{IE}\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow MD=MN\RightarrowĐpcm\)