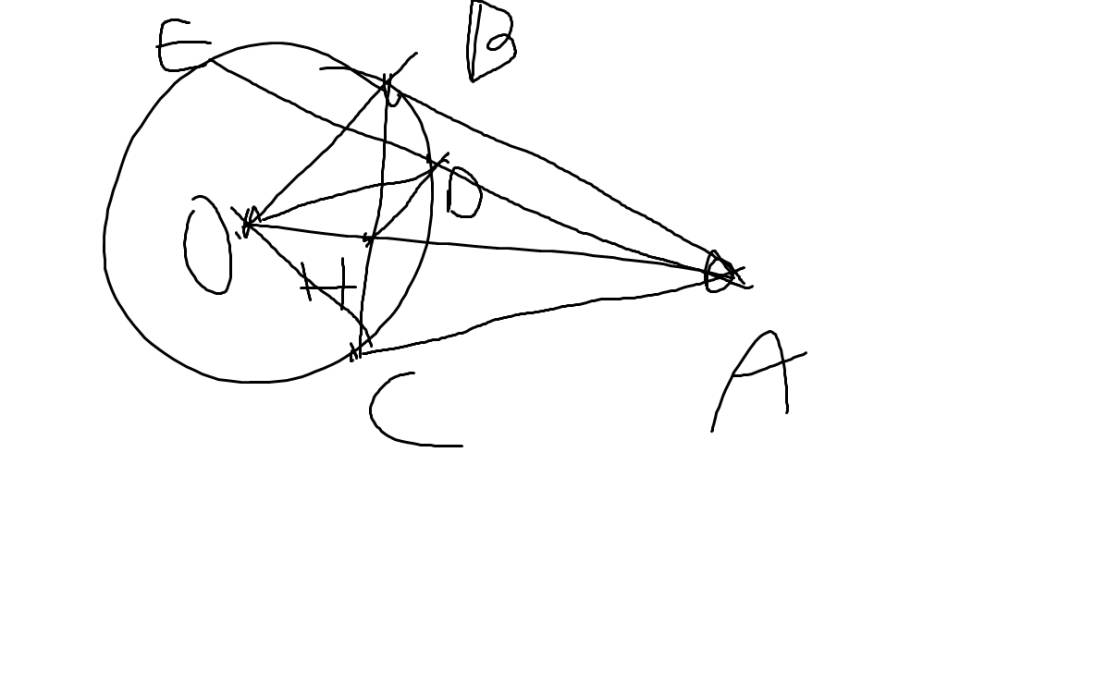
Từ A nằm ngoài [ ở] kẻ tiếp tuyến AB, AC và cát tuyến ADE với [ ô] . Gọi H là trung điểm DE
a, CM ; tứ giác ABOC ; ABHO nội tiếp
b , CM ; AB2 = AD . AE
c , Gọi I là giao điểm của OA với BC . CM ; \(\Delta\) AID \(\wr\) \(\Delta\) AEO
d, Kẻ qua D đường thảng \(\perp\) với OB cắt BC , BE lần lượt tại K và F . CM ; DKHC nội tiếp