cho ΔABC có \(\widehat{B}\) +\(\widehat{C}\) = 105 ; AB + AC\(\sqrt{2}\)= 2BC . Tính \(\widehat{B}\) và \(\widehat{C}\)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
ML
Những câu hỏi liên quan
cho tam giác ABC vuông tại C có \(\widehat{A}< \widehat{B}\). gọi I, O thứ tự là tâm đường tròn nội tiếp, ngoại tiếp ΔABC. biết ΔBIO vuông . tính tỉ số các cạnh của ΔABC
Trong ΔABC,ΔABC, kẻ AH⊥BC(H∈BC) sao cho \(\widehat{BAH}\)= \(2\widehat{CAH}\). Tính \(\widehat{B}\); \(\widehat{C}\) biết \(\widehat{A}=72^O\). (VẼ CẢ HÌNH)
Cho ΔABC vuông tại A, biết AB 6cm; AC 8cm. a) Tính độ dài cạnh BC, so sánh widehat{B} và widehat{C}. b) Vẽ trung tuyến AM của ΔABC. Trên tia đối của tia MA lấy điểm E sao cho ME MA. Chứng minh: ΔMAB ΔMEC và widehat{ACE} 90 độ. c) Gọi H là trung điểm của cạnh AC, chứng minh: HB HE. d) HB cắt AE tại P, HE cắt BC tại Q, chứng minh: ΔHPQ cân.
Đọc tiếp
Cho ΔABC vuông tại A, biết AB = 6cm; AC = 8cm.
a) Tính độ dài cạnh BC, so sánh \(\widehat{B}\) và \(\widehat{C}\).
b) Vẽ trung tuyến AM của ΔABC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA. Chứng minh: ΔMAB = ΔMEC và \(\widehat{ACE}\) = 90 độ.
c) Gọi H là trung điểm của cạnh AC, chứng minh: HB = HE.
d) HB cắt AE tại P, HE cắt BC tại Q, chứng minh: ΔHPQ cân.
Cho ΔABC vuông tại A có AB =3cm AC =4cm, kẻ đường cao AH (H ∈ BC)
a) Tính BC.
b) So sánh \(\widehat{B}\) và \(\widehat{C}\); HB và HC.
Help me câu b).
Vì ΔABC vuông tại A
==> BC2 = AC2 +AB2 ( Định lý Pitago )
BC2 = 42 + 32
BC2 = 27
==> BC = √27
Đúng 0
Bình luận (0)
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
Vậy: BC=5cm
Đúng 0
Bình luận (0)
b) Xét ΔABC có AC>AB(4cm>3cm)
mà góc đối diện với cạnh AC là \(\widehat{ABC}\)
và góc đối diện với cạnh AB là \(\widehat{ACB}\)
nên \(\widehat{B}>\widehat{C}\)(Định lí quan hệ giữa cạnh và góc đối diện trong tam giác)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho ΔABC vuông tại A (AB < AC)
Kẻ \(AH\perp BC\) tại H
a) Chứng minh \(\widehat{ABC}\) = \(\widehat{HAC}\)
b) Chứng minh \(\widehat{ACB}\) = \(\widehat{HAB}\)
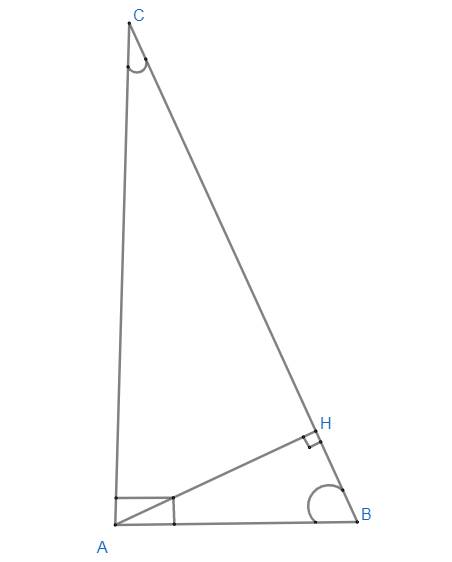
a)
Xét 2 tam giác vuông ABC và HAC có:
\(\widehat{C}\) chung
=> tg ABC \(\sim\) td HAC (g.g)
=> \(\widehat{ABC}=\widehat{HAC}\)
b)
Xét 2 tg vuông ACB và HAB có:
\(\widehat{B}\) chung
=> tg ACB \(\sim\) tg HAB (g.g)
=> \(\widehat{ACB}=\widehat{HAB}\)
Đúng 2
Bình luận (2)
Cho tam giác ABC có \(BC=2cm\), \(\widehat{A}=105^o\), \(\widehat{C}=30^o\). Tính diện tích tam giác ABC.
Có \(\widehat{B}=180^0-105^0-30^0=45^0\)
Kẻ AH vuông góc với BC
\(\Rightarrow\Delta ABH\) là tam giác vuông cân tại A
\(\Rightarrow AH=BH\)
Có \(tanC=\dfrac{AH}{HC}\Leftrightarrow HC=\dfrac{AH}{tan30^0}=\sqrt{3}AH\)
\(\Rightarrow BH+CH=AH+\sqrt{3}AH\Leftrightarrow BC=\left(1+\sqrt{3}\right)AH\)\(\Leftrightarrow AH=\dfrac{BC}{1+\sqrt{3}}=\dfrac{2}{1+\sqrt{3}}\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.\dfrac{2}{1+\sqrt{3}}.2=\dfrac{2}{1+\sqrt{3}}\) (cm2)
Vậy...
Đúng 3
Bình luận (0)
cho ΔABC có hai đường phân giác AD và BE. CMR:
a) Nếu \(\widehat{ADC}=\widehat{BEC}\) thì \(\widehat{BAC}=\widehat{ABC}\)
b) Nếu \(\widehat{ADC}=\widehat{BEC}\) thì \(\widehat{BAC}+\widehat{ABC}=120^o\)
Cho \(\Delta ABC\)có \(\widehat{B}=30^o;\widehat{C}=105^o\)và D là trung điểm của BC. Tính số đo của \(\widehat{BAD}\).
Cho ΔABC có AB = 14cm, AC = 28cm. Trên cạnh AC lấy điểm D sao cho: AD = 7cm. CMR: \(\widehat{ABD}\) = \(\widehat{ACB}\)
Xét ΔABD và ΔACB có
AB/AC=AD/AB
góc A chung
=>ΔABD đồng dạng với ΔACB
=>góc ABD=góc ACB
Đúng 1
Bình luận (0)
cho ΔABC có \(\widehat{A}=60^o\). đaẹt BC=a; CA=b; AB=c. CMR: \(\dfrac{1}{a+b}+\dfrac{1}{a+c}=\dfrac{3}{a+b+c}\)
Đẳng thức cần chứng minh tương đương với:
\(\dfrac{2a+b+c}{\left(a+b\right)\left(a+c\right)}=\dfrac{3}{a+b+c}\)
\(\Leftrightarrow\left(2a+b+c\right)\left(a+b+c\right)=3\left(a^2+ab+bc+ca\right)\)
\(\Leftrightarrow2a^2+b^2+c^2+3ab+3ac+2bc=3a^2+3ab+3bc+3ca\)
\(\Leftrightarrow a^2=b^2+c^2-bc\).
Đây chính là định lý hàm cos cho tam giác ABC có \(\widehat{A}=60^o\).
(Phần chứng minh bạn có thể xem ở Cho tam giác ABC có Â=60 độ. Chứng minh rằng BC^2=AB^2 AC^2-AB.BC - Hoc24)
Đúng 0
Bình luận (0)





