Cho các đường thẳng : \(y=x-2\left(d_1\right)\) ; \(y=2x-4\left(d_2\right)\) ; \(y=mx+\left(m+2\right)\left(d_3\right)\)
a. Chứng tỏ rằng \(\left(d_3\right)\) luôn đi qua một điểm cố định.
b. Chứng tỏ ba đường thẳng đồng quy.
Bài 1: Cho 3 đường thẳng: \(\left(d_1\right)y=2x-1\); \(\left(d_2\right)y=3x-2\); \(\left(d_3\right)y=x+1\). Tìm m để 2 đường thẳng \(\left(d_1\right)\) và \(\left(d_2\right)\) cắt nhau tại một điểm nằm trên đường thẳng \(\left(d_3\right)\)
Cho các đường thẳng \(y=x+1\left(d_1\right),y=3x-2\left(d_2\right),y=2m+3x-1\left(d_3\right)\)
a) Vẽ đồ thị hàm số \(\left(d_1\right),\left(d_2\right)\) trên cùng hệ trục tọa độ
b) Tìm m để 3 đường thẳng đồng quy
c) Cm rằng \(\left(d_3\right)\) để luôn đi qua 1 điểm với mọi giá trị của m
a: 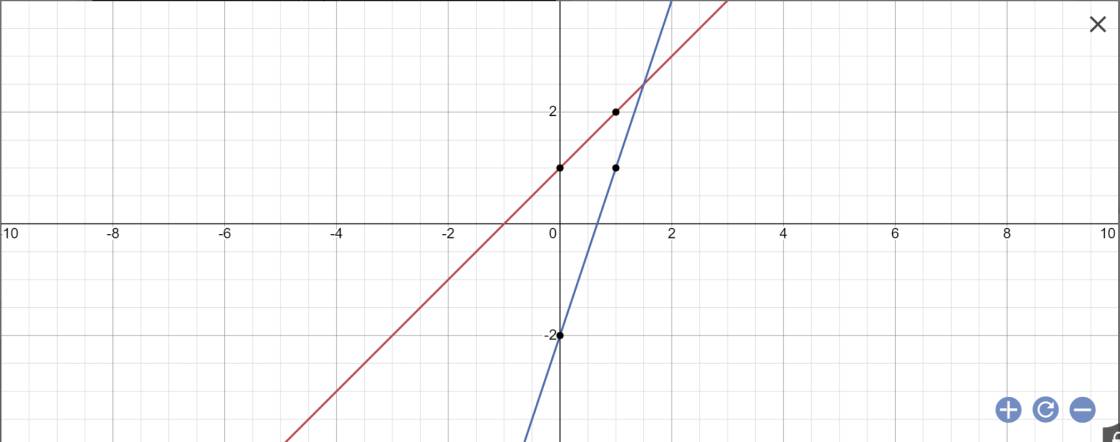
b: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}3x-2=x+1\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-x=2+1\\y=x+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=3\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=\dfrac{3}{2}+1=\dfrac{5}{2}\end{matrix}\right.\)
Thay x=3/2 và y=5/2 vào (d3), ta được:
\(2m+3\cdot\dfrac{3}{2}-1=\dfrac{5}{2}\)
=>\(2m+\dfrac{7}{2}=\dfrac{5}{2}\)
=>\(2m=-1\)
=>m=-1/2
c: (d3): y=2m+3x-1
=>y=m*2+3x-1
Tọa độ điểm mà (d3) luôn đi qua là:
\(\left\{{}\begin{matrix}2=0\left(vôlý\right)\\y=3x-1\end{matrix}\right.\)
=>(d3) không đi qua cố định bất cứ điểm nào
Bài 1: Cho 2 đường thẳng \(\left(d_1\right)y=2x-1\); \(\left(d_2\right)y=x+2\)
a, Vẽ 2 đường thẳng \(\left(d_1\right)\)và \(\left(d_2\right)\) trên cùng 1 mặt phẳng tọa độ
b, Xác định tọa độ giao điểm của \(\left(d_1\right)\) và \(\left(d_2\right)\) bằng phép toán
c, Viết phương trình đường thẳng \(\left(d\right)y=ax+b\). Biết \(\left(d\right)//\left(d_1\right)\) và cắt trục hoành tại điểm có hoành độ bằng 1
a: 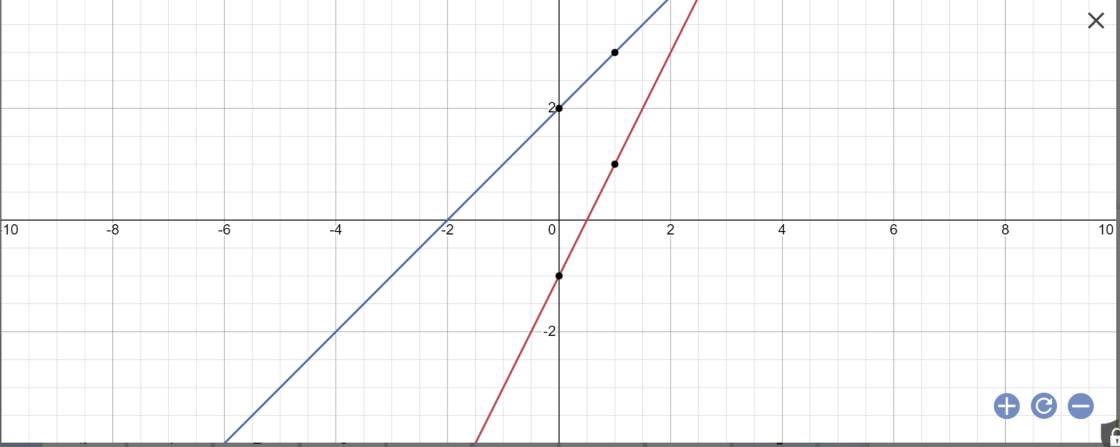
b: Phương trình hoành độ giao điểm là:
2x-1=x+2
=>x=3
Thay x=3 vào y=x+2, ta được:
y=3+2=5
c: Vì (d)//(d1) nên (d): y=2x+b
Thay x=1 và y=0 vào (d), ta được:
b+2=0
=>b=-2
=>y=2x-2
Cho hai đường thẳng \(\left(d_1\right)\):\(y=\left(m^2-1\right)x+m^2-5\) với \(\left(m\ne\pm1\right)\); \(\left(d_2\right):x+1\);\(\left(d_3\right):y=-x+3.\).Xác định m để 3 đường thẳng \(d_1\),\(d_2\),\(d_3\) đồng quy
Tọa độ giao điểm của (d2) và (d3) là nghiệm của hệ phương trình sau:
\(\left\{{}\begin{matrix}x+1=-x+3\\y=x+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=2\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Thay x=1 và y=2 vào (d1), ta được:
\(\left(m^2-1\right)+m^2-5=2\)
=>\(2m^2=8\)
=>\(m^2=4\)
=>\(\left[{}\begin{matrix}m=2\\m=-2\end{matrix}\right.\)
Bài 1: trên mặt phẳng tọa độ \(O_{xy}\), cho 2 đường thẳng \(\left(d_1\right)y=x-3;\left(d_2\right)y=-3x+1\)
a, Vẽ \(\left(d_1\right);\left(d_2\right)\) trên cùng 1 mặt phẳng tọa độ
b, Viết phương trình đường thẳng\(\left(d\right)y=ax+b\) biết \(\left(d\right)//\left(d_1\right)\) và cắt trục tung tại điểm có hoành độ bằng 7
Bài 2: Cho hàm số bậc nhất \(y=\left(m-1\right)x+m-3\) \(\left(m\ne1\right)\)\(\left(d\right)\)
a, Tìm m để (d) cắt trục tung tại điểm có tung độ bằng 1
b,Gọi A, B lần lượt là giao của (d) với 2 trục tọa độ. Tìm m để △OAB cân
Mọi người giúp mình hai bài này với, mình cần gấp
1:
b: Vì (d)//(d1) nên (d): y=x+b
Thay x=7 và y=0 vào (d), ta được:
b+7=0
=>b=-7
=>y=x-7
a: 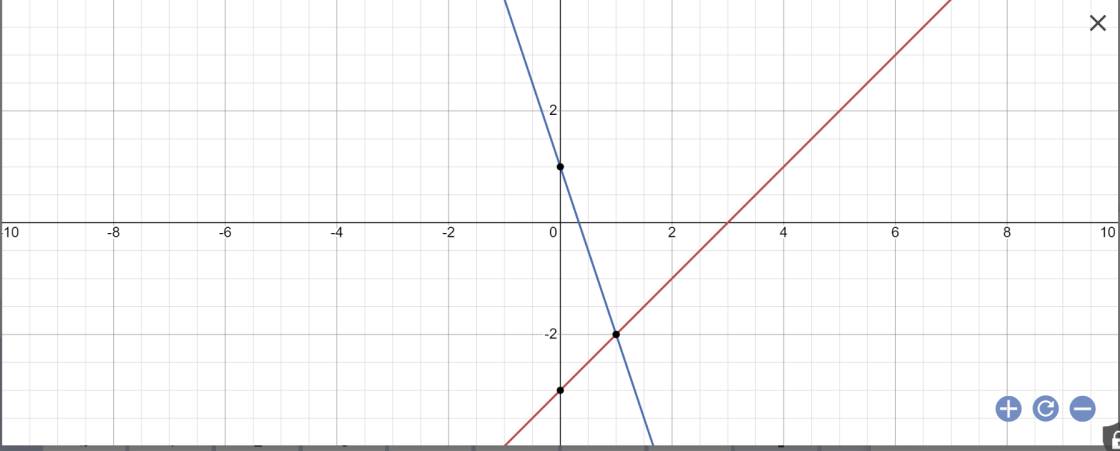
Trên mặt phẳng tọa độ Oxy, cho hai đường thẳng \(\left(d_1\right):y=\left(m^2+1\right)x-2\) và \(\left(d_2\right):y=\left(m+3\right)x-m-2\) (m là tham số). Tìm m để \(\left(d_1\right),\left(d_2\right)\) cắt nhau tại \(M\left(x_M;y_M\right)\) thỏa \(A=2020x_M\left(y_M+2\right)\) đạt giá trị nhỏ nhất.
Tình cờ hay cố ý mà dữ liệu bài toán có rất nhiều sự trùng hợp dẫn đến lời giải rất dễ dàng:
\(M\in d_1\Rightarrow y_M=\left(m^2+1\right)x_M-2\Rightarrow y_M+2=\left(m^2+1\right)x_M\)
\(\Rightarrow A=2020\left(m^2+1\right)x_M^2\ge0\)
\(A_{min}=0\) khi \(m=0\)
Khi đó điểm M là \(M\left(0;-2\right)\)
Tính góc giữa các đường thẳng sau:
a) \(d_1:3x-4y=0\) và \(d_2:\left\{{}\begin{matrix}x=1+3t\\y=-4t\end{matrix}\right.\)
b) \(d_1:\dfrac{x}{1}=\dfrac{y+2}{-2}\) và \(d_2:\left\{{}\begin{matrix}x=5+3t\\t=1-t\end{matrix}\right.\)
8. Cho các đường thẳng
\(d:y=\left(m-2\right)x+m+7;\)
\(d_1:y=-mx-3+2m;\)
\(d_2:y=-m^2x-2m+1;\)
\(d_3:y=-\dfrac{2}{3}x+\dfrac{5}{3};\)
\(d_4:y=-\dfrac{1}{6}\left(m+3\right)x=+4.\)
Tìm m để
a.\(d//d_1\)
b.\(d\equiv d_2\)
c.\(d\) cắt \(d_3\) tại điểm có tung độ \(y=\dfrac{1}{3}\)||
d. \(d\perp d_4\)
a: d//d1
=>m-2=-m và m+7<>2m-3
=>m=1
b: d trùng với d2
=>m-2=-m^2 và m+7=-2m+1
=>m=-2 và m^2+m-2=0
=>m=-2
d: d vuông góc d4
=>-1/6(m+3)(m-2)=-1
=>(m+3)(m-2)=6
=>m^2+m-6-6=0
=>m^2+m-12=0
=>m=-4 hoặc m=3
c: Thay y=1/3 vào d3, ta được:
-2/3x+5/3=1/3
=>-2/3x=-4/3
=>x=2
Thay x=2 và y=1/3 vào (d), ta được:
2(m-2)+m+7=1/3
=>3m+3=1/3
=>3m=-8/3
=>m=-8/9
Cho hai đường thẳng \(y=-4x+m-1\left(d_1\right)\) và \(y=\dfrac{4}{3}x+15-3x\left(d_2\right)\)
a, Tìm m để đường thẳng \(\left(d_1\right)\) và (\(\left(d_2\right)\) cắt nhau tại một điểm C trên trục tung.
b, Với m ở trên hãy tìm tọa độ giao điểm A,B của 2 đường thẳng \(\left(d_1\right),\left(d_2\right)\) với trục hoành.
b: Để hai đường thẳng cắt nhau tại một điểm trên trục tung thì m-1=15
hay m=16
Cho các hàm số y=x(d\(_1\)), y=2x(d\(_2\)), y=-x+3(\(d_3\))
a) Vẽ trên cùng một hệ trục các đồ thị (d\(_1\)), (\(d_2\)), (\(d_3\))
b) Đường thẳng d\(_3\) cắt các đường thẳng \(\left(d_1\right),\left(d_2\right)\) lần lượt tại A và B. Tính toạ độ các điểm A, B và diện tích tam giác OAB.
a, Bạn tự vẽ
b, PT hoành độ giao điểm (d1) và (d3) là
\(x=-x+3\Leftrightarrow x=\dfrac{3}{2}\Leftrightarrow y=\dfrac{3}{2}\Leftrightarrow A\left(\dfrac{3}{2};\dfrac{3}{2}\right)\Leftrightarrow OA=\sqrt{\left(\dfrac{3}{2}-0\right)^2+\left(\dfrac{3}{2}-0\right)^2}=\dfrac{3\sqrt{2}}{2}\)
PT hoành độ giao điểm (d2) và (d3) là
\(2x=-x+3\Leftrightarrow x=1\Leftrightarrow y=2\Leftrightarrow B\left(1;2\right)\Leftrightarrow OB=\sqrt{\left(1-0\right)^2+\left(2-0\right)^2}=\sqrt{5}\)
Ta có \(AB=\sqrt{\left(\dfrac{3}{2}-1\right)^2+\left(\dfrac{3}{2}-2\right)^2}=\sqrt{\dfrac{1}{4}+\dfrac{1}{4}}=\dfrac{\sqrt{2}}{2}\)
Ta có \(OA^2+AB^2=\dfrac{9}{2}+\dfrac{1}{2}=\dfrac{10}{2}=5=OB^2\) nên tg OAB vuông tại A
Do đó \(S_{OAB}=\dfrac{1}{2}\cdot OA\cdot AB=\dfrac{1}{2}\cdot\dfrac{3\sqrt{2}}{2}\cdot\dfrac{\sqrt{2}}{2}=\dfrac{3}{4}\left(đvdt\right)\)