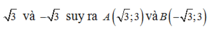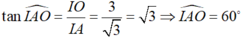Cho parabol (P) có đỉnh ở gốc tọa độ O và đi qua điểm A (1; \(\frac{-1}{4}\))
a) Viết phương trình của P
b) Viết phương trình của đường thẳng d song song cới đường thẳng x+2y=1 và đi qua điểm B(0;m). Với giá trị nào của m thì đường thẳng d cắt parabol P tại hai điểm có hoành độ \(x_1\) và \(x_2\), sao cho thõa mản : \(3x_1+5x_2=5\)