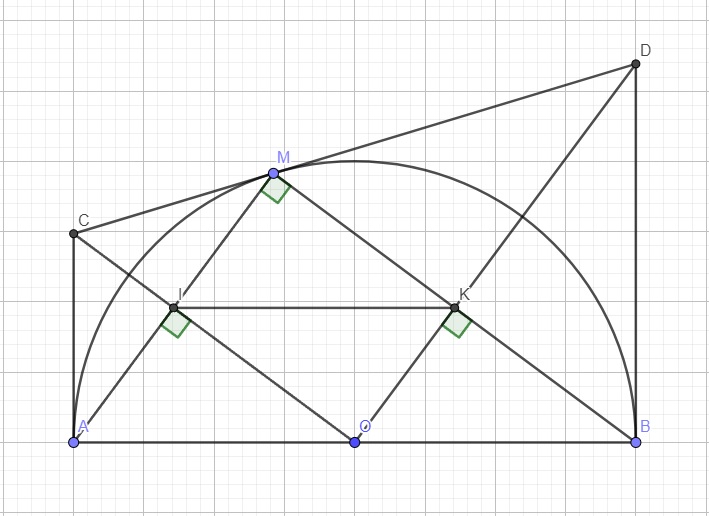
Do C là giao 2 tiếp tuyến tại M và A nên \(CM=CA\)
Lại có \(OM=OA=R\)
\(\Rightarrow OC\) là trung trực của AM
\(\Rightarrow I\) là trung điểm AM và \(OC\perp AM\) tại I
Tương tự, ta có OD là trung trực BM nên K là trung điểm BM và \(OD\perp BM\) tại K
\(\Rightarrow\) IK là đường trung bình tam giác MAB
\(\Rightarrow IK||AB\Rightarrow\widehat{MIK}=\widehat{MAB}\) (đồng vị)
Mà \(\widehat{MAB}+\widehat{MBA}=90^0\) (do \(\widehat{AMB}=90^0\) góc nt chắn nửa đường tròn)
\(\Rightarrow\widehat{MIK}+\widehat{MBA}=90^0\) (1)
DB là tiếp tuyến tại B \(\Rightarrow\widehat{DBO}=90^0\Rightarrow\widehat{ODB}=\widehat{MAB}\) (cùng phụ \(\widehat{OKB}\)) (2)
Theo t/c hai tiếp tuyến cắt nhau, \(\widehat{ODB}=\widehat{ODC}\) (3)
\(\left(1\right);\left(2\right);\left(3\right)\Rightarrow\widehat{MIK}+\widehat{ODC}=90^0\)
\(\Rightarrow\widehat{CIK}+\widehat{ODC}=\widehat{CIM}+\widehat{MIK}+\widehat{ODC}=90^0+90^0=180^0\)
\(\Rightarrow CIKD\) nội tiếp