Ôn tập góc với đường tròn

a: Xét tứ giác OAIE có \(\widehat{OEI}=\widehat{OAI}=90^0\)

nên OAIE là tứ giác nội tiếp

Xét tứ giác OEKB có \(\widehat{OEK}+\widehat{OBK}=90^0+90^0=180^0\)

nên OEKB là tứ giác nội tiếp

b: Ta có: OAIE là tứ giác nội tiếp

=>\(\widehat{OIE}=\widehat{OAE}=\widehat{OAB}\)(1)

Ta có: OEKB là tứ giác nội tiếp

=>\(\widehat{OKE}=\widehat{OBE}=\widehat{OBA}\)(2)

Ta có: ΔOAB cân tại O

=>\(\widehat{OAB}=\widehat{OBA}\)(3)

Từ (1),(2),(3) suy ra \(\widehat{OKE}=\widehat{OIE}\)

=>ΔOKI cân tại O

c: Xét ΔOAI vuông tại A và ΔOBK vuông tại B có

OI=OK

OA=OB

Do đó: ΔOAI=ΔOBK

=>AI=BK

a: Xét (O) có

ΔACB nội tiếp

AB là đường kính

Do đó: ΔACB vuông tại C

Xét tứ giác ICBH có \(\widehat{ICB}+\widehat{IHB}=90^0+90^0=180^0\)

nên ICBH là tứ giác nội tiếp đường tròn đường kính IB

Tâm là trung điểm của IB

Bán kính là \(\dfrac{IB}{2}\)

b: Xét (O) có

\(\widehat{ACD}\) là góc nội tiếp chắn cung AD

\(\widehat{ABD}\) là góc nội tiếp chắn cung AD

Do đó: \(\widehat{ACD}=\widehat{ABD}\)

mà \(\widehat{ABD}=\widehat{ICH}\)(ICBH là tứ giác nội tiếp)

nên \(\widehat{ACD}=\widehat{ICH}=\widehat{ACH}\)

=>CA là phân giác của góc HCD

a. Em tự giải

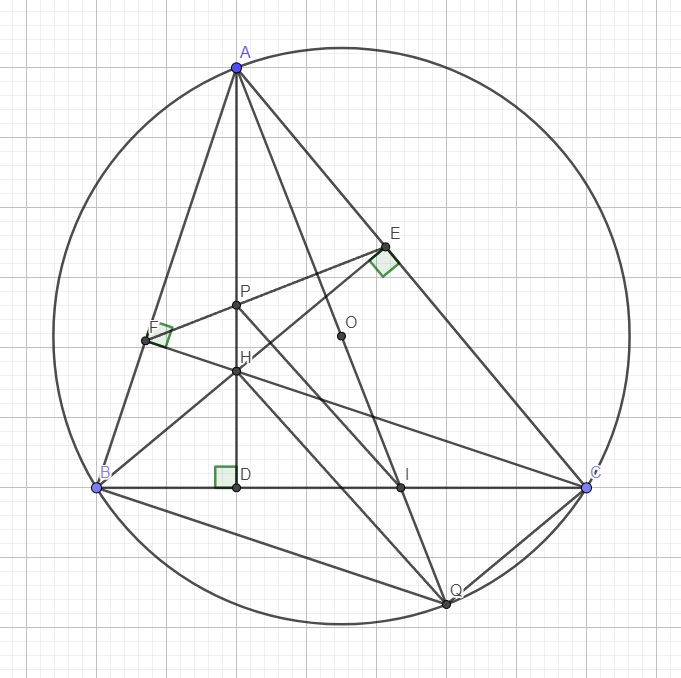
b.

Ta có: \(\widehat{ABC}=\widehat{AQC}\) (cùng chắn AC) (1)

Do AQ là đường kính \(\Rightarrow\widehat{ACQ}\) là góc nt chắn nửa đường tròn

\(\Rightarrow\widehat{ACQ}=90^0\) \(\Rightarrow\widehat{ACQ}+\widehat{CAQ}=90^0\) (2)

Tam giác ABD vuông tại D \(\Rightarrow\widehat{BAD}+\widehat{ABC}=90^0\) (3)

(1);(2);(3) \(\Rightarrow\widehat{CAQ}=\widehat{BAD}\)

c.

\(\left\{{}\begin{matrix}\widehat{PAE}=\widehat{PAI}+\widehat{CAQ}\\\widehat{IAB}=\widehat{PAI}+\widehat{BAD}\\\widehat{CAQ}=\widehat{BAD}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\widehat{PAE}=\widehat{IAB}\) (3)

Tứ giác BCEF nội tiếp (E và F cùng nhìn BC dưới 1 góc vuông)

\(\Rightarrow\widehat{ABI}+\widehat{CEF}=180^0\)

Mà \(\widehat{CEF}+\widehat{AEP}=180^0\)

\(\Rightarrow\widehat{AEP}=\widehat{ABI}\) (4)

(3);(4) \(\Rightarrow\Delta AEP\sim\Delta ABI\left(g.g\right)\)

\(\Rightarrow\dfrac{AP}{AI}=\dfrac{AE}{AB}\) (5)

AQ là đường kính \(\Rightarrow\widehat{ABQ}\) là góc nt chắn nửa đường tròn \(\Rightarrow\widehat{ABQ}=90^0\)

Xét 2 tam giác ABQ và AEH có: \(\left\{{}\begin{matrix}\widehat{ABQ}=\widehat{AEH}=90^0\\\widehat{BAQ}=\widehat{EAH}\left(\text{theo (3)}\right)\end{matrix}\right.\)  \(\Rightarrow\Delta ABQ\sim\Delta AEH\left(g.g\right)\)

\(\Rightarrow\dfrac{AE}{AB}=\dfrac{AH}{AQ}\) (6)

(5);(6) \(\Rightarrow\dfrac{AH}{AQ}=\dfrac{AP}{AI}\) \(\Rightarrow\dfrac{AP}{AH}=\dfrac{AI}{AQ}\)

\(\Rightarrow PI||HQ\) (định lý Talet đảo)

a: Xét (O) có

NB,NM là các tiếp tuyến

Do đó: NB=NM

=>N nằm trên đường trung trực của BM(1)

Ta có: OM=OB

=>O nằm trên đường trung trực của MB(2)

Từ (1) và (2) suy ra NO là đường trung trực của MB

=>NO\(\perp\)MB

Xét (O) có

ΔAMB nội tiếp

AB là đường kính

Do đó: ΔAMB vuông tại M

=>AM\(\perp\)MB

Ta có: AM\(\perp\)MB

NO\(\perp\)MB

Do đó: AM//ON

b: Ta có: ΔOAK cân tại O

mà OC là đường cao

nên OC là phân giác của góc AOK

Xét ΔOAC và ΔOKC có

OA=OK

\(\widehat{AOC}=\widehat{KOC}\)

OC chung

Do đó: ΔOAC=ΔOKC

=>\(\widehat{OAC}=\widehat{OKC}\)

=>\(\widehat{OKC}=90^0\)

=>CK là tiếp tuyến của (O)

c:

Xét (O) có D,M,B,E cùng thuộc (O)

nên DMBE là tứ giác nội tiếp

=>\(\widehat{CEB}+\widehat{DMB}=180^0\)

Ta có: \(\widehat{CMD}+\widehat{DMB}=180^0\)(hai góc kề bù)

\(\widehat{CEB}+\widehat{DMB}=180^0\)(cmt)

Do đó: \(\widehat{CMD}=\widehat{CEB}\)

a: Xét (O) có

IB,IA là tiếp tuyến

=>IB=IA và IO là phân giác của góc BIA(1)

Xét (O') có

IA,IC là tiếp tuyến

=>IA=IC và IO' là phân giác của góc AIC(2)

=>IB=IA=IC

b: Xét ΔABC có

AI là trung tuyến

AI=BC/2

=>ΔABC vuông tại A

c: Từ (1), (2) suy ra góc OIO'=1/2*góc BIC=90 độ

a: góc DMC+góc AMC=180 độ

góc ABC+góc AMC=180 độ

=>góc DMC=góc ABC

b: AC=BC

mà góc NAC=góc NBC và NC chung

nên ΔAMC=ΔBNC

=>MC=NC

a: góc AEH+góc AFH=180 độ

=>AEHF nội tiếp

b: Xet ΔBDH vuông tại D và ΔBEC vuông tại E có

góc DBH chung

=>ΔBDH đồng dạng với ΔBEC

=>BH/BC=DH/EC

=>BH*EC=DH*BC

a: góc BEC=1/2*180=90 độ

=>CE vuông góc AB

góc BDC=1/2*180=90 độ

=>BD vuông góc AC

góc AEH=góc ADH=90 độ

=>AEHD nội tiếp

b:

Gọi K là trung điểm của AH

=>K là tâm đường tròn ngoại tiếp tứ giác ADHE

góc KDO=góc KDH+góc ODH

=góc KHD+góc OBD

=90 độ

=>OD là tiếp tuyến của (K)

a: góc AOD=180-2*25=130 độ

=>góc BOD=50 độ

b: Độ dài cung AD là:

\(pi\cdot4\cdot\dfrac{130}{360}=pi\cdot\dfrac{130}{90}=\dfrac{13}{9}pi\)

a: góc IED+góc ICD=180 độ

=>IEDC nội tiếp

b: góc ECI=góc BDA=1/2*sđ cung BA

=>góc ECI=góc BCI

=>CI là phân giác của góc BCE