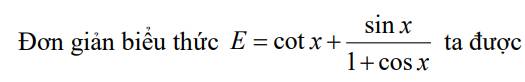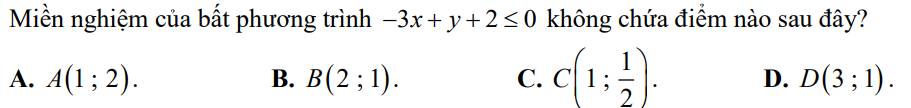Giải phương trình √2xᒾ-3x-5 =√xᒾ-7
Ôn tập chương III
\(\sqrt{2x^2-3x-5}=\sqrt{x^2-7}\)
Bình phương 2 vế pt , ta có :
\(2x^2-3x-5=x^2-7\)
\(\Rightarrow2x^2-x^2-3x=-7+5\)
\(\Rightarrow x^2-3x-2=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{17}}{2}\\x=\dfrac{3-\sqrt{17}}{2}\end{matrix}\right.\)
Thay lần lượt các giá trị trên vào pt , ta thấy không có giá trị nào thỏa mãn
Vậy pt vô nghiệm
Đúng 1
Bình luận (0)
=>2x^2-3x-5=x^2-7
=>x^2-3x+2=0
=>x=2(loại) hoặc x=1(loại)
Đúng 1
Bình luận (0)
Tìm khoảng cách từ điểm O(0;0) đến đg thẳng denta : x /6+y/8=1
A 4,8
B 1/10
C 1/14
D 48/căn14
 làm giúp mình bài 3 vớiiii :<
làm giúp mình bài 3 vớiiii :<
\(\overrightarrow{AB}.\overrightarrow{AC}=AB.AC.cos\widehat{BAC}=a.a.cos60^0=\dfrac{a^2}{2}\)
\(\overrightarrow{AB}.\overrightarrow{AM}=AB.AM.cos\widehat{BAM}=a.\dfrac{a\sqrt{3}}{2}.cos30^0=\dfrac{3a^2}{4}\)
\(\overrightarrow{AB}.\overrightarrow{BC}=AB.BC.cos\left(180^0-\widehat{ABC}\right)=a.a.cos120^0=-\dfrac{a^2}{2}\)
\(\overrightarrow{AC}.\overrightarrow{BM}=\overrightarrow{AC}.\dfrac{1}{2}\overrightarrow{BC}=\dfrac{1}{2}AC.BC.cos\widehat{ACB}=\dfrac{1}{2}a.a.cos60^0=\dfrac{a^2}{4}\)
Đúng 3
Bình luận (0)
Hầm số \(y=\dfrac{1}{\sqrt{x+3m-x}+\sqrt{m+2-x}}\) xác định với ∀\(x\) ∈ \(\left[-1;1\right]\)
Ai đó giúp mik giải vs 👉👈
\(=\dfrac{cosx}{sinx}+\dfrac{sinx}{1+cosx}\)
\(=\dfrac{cosx+cos^2x+sin^2x}{sinx\left(1+cosx\right)}=\dfrac{cosx+1}{sinx\left(1+cosx\right)}=\dfrac{1}{sinx}\)
Đúng 1
Bình luận (0)
Lời giải:
\(E=\cot x+\frac{\sin x}{1+\cos x}=\frac{\cos x}{\sin x}+\frac{\sin x}{1+\cos x}=\frac{\cos x(1+\cos x)+\sin ^2x}{\sin x(\cos x+1)}\)
\(=\frac{\cos x+\sin ^2x+\cos ^2x}{\sin x(\cos x+1)}=\frac{\cos x+1}{\sin x(\cos x+1)}=\frac{1}{\sin x}\)
Đúng 0
Bình luận (0)
Chọn A.
\(-3\cdot1+2+2=1>0\) nên \(A\left(1;2\right)\) không thuộc miền nghiệm của bất phương trình đã cho.
Đúng 0
Bình luận (0)
\(\dfrac{4x^2+3x-1}{x^2+5x+7}>0\)
\(\dfrac{x^2-3x+2}{x^2-4x+3}>0\)
`[4x^2+3x-1]/[x^2+5x+7] > 0`
Mà `x^2+5x+7 > 0 AA x`
`=>4x^2+3x-1 > 0`
`<=>(4x-1)(x+1) > 0`
`<=>[(x < -1),(x > 1/4):}`
_________________________________________
`[x^2-3x+2]/[x^2-4x+3] > 0`
Xét `x^2-3x+2=0<=>[(x=2),(x=1):}`
`x^2-4x+3=0<=>[(x=3),(x=1):}`
Đặt `[x^2-3x+2]/[x^2-4x+3]=f(x)`
BXD:
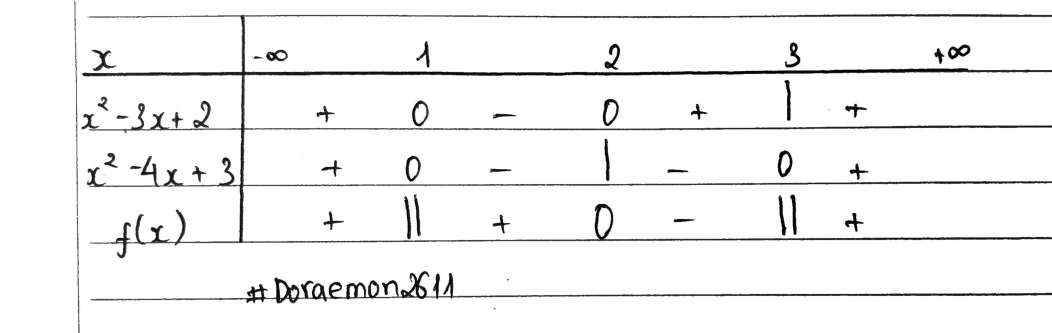
`=>f(x) > 0<=>x in (-oo;1)uu(1;2)uu(3;+oo)`
Đúng 3
Bình luận (0)
Có hai địa điểm A,B cùng nằm trên một tuyến đường quốc lộ thẳng. Khoảng cách A và B là 30,5km. Một xe máy xuất phát từ A lúc 7 giờ theo chiều từ A đến B. Lúc 9 giờ, một ô tô xuất phát từ B chuyển động thẳng đều với vận tốc 80 km/h theo cùng chiều với xe máy. Chọn A làm mốc, cho thời điểm 7 giờ làm mốc thời gian và chọn chiều từ A đến B làm chiều dương, Phương trình chuyển động của xe máy là y2t^2+36t, trong đó y tính bằng km, t tính bằng giờ. Biết rằng đến lúc ô tô đuổi kịp xe máy thì hai xe dừn...
Đọc tiếp
Có hai địa điểm \(A,B\) cùng nằm trên một tuyến đường quốc lộ thẳng. Khoảng cách \(A\) và \(B\) là \(30,5km\). Một xe máy xuất phát từ \(A\) lúc \(7\) giờ theo chiều từ \(A\) đến \(B\). Lúc \(9\) giờ, một ô tô xuất phát từ \(B\) chuyển động thẳng đều với vận tốc \(80\) km/h theo cùng chiều với xe máy. Chọn \(A\) làm mốc, cho thời điểm \(7\) giờ làm mốc thời gian và chọn chiều từ \(A\) đến \(B\) làm chiều dương, Phương trình chuyển động của xe máy là \(y=2t^2+36t\), trong đó \(y\) tính bằng km, \(t\) tính bằng giờ. Biết rằng đến lúc ô tô đuổi kịp xe máy thì hai xe dừng lại và vị trí đó cách điểm B là \(x\) \(km\). Tính \(x\) \(km\).
Giúp em ạ, em cần gấp
Mọi người giúp mình ạ!
Câu a và câu b